1. The Model

There is a pool of identical research firms standing ready to participate in the following contest. At date t = 0, the sponsor invites N ≥ 2 firms to enter the tournament. Each firm is required to pay an entry fee E in order to compete for a fixed monetary prize P > 0. If fewer than two firms enter, the contest is called off. Otherwise, the prize is awarded to the contestant that has produced the innovation of the highest value to the sponsor at t = 2. If more than 1 firms are tied with the best innovation, then the winner is randomly selected from among them with equal probability. At date t = 1, the cost of conducting research, which is independent across firms, is realized for each firms, and firm's decision to conduct research is taken. The sequence of this model is depicted in Figure 1.

[Figure 1]

Sequence of the Play

When a firm conducts research, then the value of innovation is realized independently. The distribution of potential innovation values when a firm conduct research is denoted by F, defined on [0, a] with F(0) = 0 and a≤∞. If a firm does not conduct research, the value of innovation is zero. The cost of conducting research in period 1 is denoted by c_i for the firm i. The distribution of cost is denoted by G, defined on [0, b] with G(0) = 0 and b≤∞. Assume that F and G have finite mean and strictly positive density f and g respectively, everywhere on domains. Thus, if firm i decides to conduct research, it bears the cost c_i and obtains a single draw, z_i, which is the value of innovation from the distribution F.

While the sponsor can evaluate the value of innovation, that value is not verifiable by a court since contract courts seldom possess the ability or expertise necessary to evaluate technical research projects. Also, research effort by firm is assumed as private information. Taylor (1995) observes that conducting a tournament can resolve these problems, as the act of exchanging the prize for an innovation can easily be verified and enforced by a court. Finally, all of the features of the model are assumed to be common knowledge among sponsor and firms.

2. Equilibrium Play and Tournament Design

The previous section describes the game where N players play with imperfect information. The strategy of each contestant is a sequence of state-dependent decisions. At t = 0, each invited firm decides whether to participate. After that, each firm decides whether to conduct research at t = 1, given the number of its rivals as well as the realization of cost. Any firm choosing not to participate the tournament receives the reservation profit, which is normalized to zero.

At t = 1, a research firm i makes research decision, which depends on the realized cost and other firms' behavior. Let's denote p_i as the probability of the event when only i among N − 1 rivals will decide to conduct research. Then, a contestant with cost level, c_i, will conduct research if and only if

Where

Note that ∏ⁱ is the probability of firm i’s winning the contest given other firms' research conduct strategies, if a firm decides to conduct research. Now, the following Lemma 1 describes the equilibrium play at t = 1.

LEMMA 1 At t = 1, there exists ĉ ∈ (0, b] such that a contestant will conduct research if and only if c_i ≤ , with other contestants' behavior fixed.

PROOF: Given other firms' strategies, 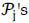and ∏ⁱ are constant at t = 1. Note that 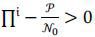. Thus, we get 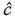> 0. ∎

If P ≥ b ∙ (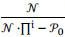), then = b, so the firm always conducts research. In other words, if b is small enough, or if the prize is large relative to the cost, then the firms in the pool always conduct research as in Taylor(1995). Otherwise, 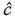= P ∙ (∏ⁱ − 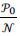) ∈ (0, b).

Lemma 1 states that the firms use pure strategy at period 1. Also, Lemma 1 guarantees the interior level of 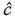, unless b is too small. The threshold level of cost, 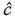, depends on the number of contestants in the pool and the relative size of the prize to b. Now we state the main result of this section.

PROPOSITION 1 The unique perfect equilibrium at t = 1 is for each contestant to adopt the same c* threshold strategy.

PROOF: Lemma 1 establishes that every firm uses a threshold strategy at t = 1, and each threshold level of cost satisfies (1) with equality given other firms' threshold levels. Then, an equilibrium of the research behavior is any vector 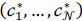satisfying the research incentive constraints, (1), for all contestants.

Let's pick any solution and consider two arbitrary firms i and j. Consider the resulting projection of these two firms' best-response functions to one another's strategies, while holding fixed the strategies of all other contestants. Let 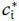(c_i) be the firm i’s best-response when the firm i’s threshold level is c_i. With (1), it can be easily shown that 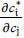< 0. Thus, we have 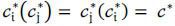, 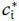(c_i) and 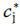(c_i) are symmetric and cross only once on the 45-degree line. This establishes uniqueness of equilibrium play on the research subgame at t = 1. ∎

We demonstrate that asymmetric equilibrium does not exist, so the game at t = 1 has a unique equilibrium which is symmetric. Even though it is not surprising that a symmetric game with identical players has a symmetric equilibrium, the absence of any asymmetric or mixed strategy equilibria is uncommon. The main advantage of uniqueness is that it ensures that the sponsor's tournament design problem is well defined. From now on, subscript i will be omitted for simplicity.

Let Φ(x) be the cumulative distribution function for the value of a contestant's innovation under the equilibrium strategy above. This is given by

The sponsor's expected payoff at the beginning of the tournament is, therefore, the collected entry fees plus the the equilibrium expected value of the best innovation net of the prize

where Φ^N(x) is the distribution of the best innovation discovered by N contestants in the tournament. By integrating by part, (3) can be written as

(4)

Now, consider the entry decision by firms at t = 0. A firm will enter the tournament if

where the left-hand side is the expected payoff when it decides to enter with N − 1 other firms. It is assumed below that, if (5) binds, all N firms enter in equilibrium.

Now, consider the tournament design by the sponsor. The optimal tournament for the sponsor maximizes the expected payoff, V, subject to the participation constraint (5), where the threshold level is determined by

or

Some important features of optimal tournament scheme can be shown. The following results describe characteristics of optimal tournament to the sponsor.

LEMMA 2 With the optimally designed tournament, the participation constraint is binding.

PROOF: Suppose the participation constraint (5) is not binding. Then, the sponsor can increase the payoff by raising the entry fee while satisfying the participation constraint. Thus, the participation constraint should be binding with optimal tournament design. ∎

PROPOSITION 2 Optimally designed tournament maximizes the social welfare.

PROOF: Social welfare at the beginning of the tournament is the expected value of highest innovation net of expected costs to the participants, or

Since (5) is binding with optimally designed tournament, the sponsor's problem becomes

max ,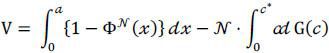

which is identical to the social welfare function. ∎

The result above is analogue to the two-part tariff in monopolistic market. The sponsor in our model behaves like a monopolist to set up the entry fee and the prize. The prize is to induce the individual contestant's effort while the entry fee is to recoup the cost of contest. However our model differs from two-part tariff in that there's only one prize awarded ever and that the sponsor limits the number of contestants directly.

Note that previous analysis is based on the assumption that the firms are not capital constrained. However, it is not rare that the contestants have only limited resource which is less than c* + E . If the contestants are capital-constrained, optimally designed tournament does not maximize the social welfare in general. In that case, the sponsor may need to set up negative entry fee or subsidy in order to get the desired level of innovation.

3. Number of Contestants and Effort Level

The foremost reason for limiting entry into tournaments1 is to raise the level of contestant effort. Nalebuff and Stiglitz (1983) showed that a reduction in the overall level of effort may be resulted by allowing too many workers to compete for a prize in labor tournaments. Taylor (1995) demonstrated, for research tournaments with homogeneous contestants, that allowing too many contestants reduces the total level of research effort and lowers the expected outcome of the tournament. If there are too many participants, contestants are discouraged from expending effort because their probability of winning becomes too small. The main purpose of a tournament is to make the firms compete so that high value of innovation will be procured. Thus, a sponsor need take account into effort-inducing effect as well as effort-reducing effect from competition when she restricts entry.

The level of threshold cost is determined by the equation

where P is pre-determined by the sponsor. Then, we can find a unique c* which satisfies (8) given any N ≥ 2. Let c(N) be the threshold cost level, which is a function of the number of contestants. For convenience, the integer constraint on the number of firms is ignored. By Implicit Function Theorem, we get

The denominator of (9) is negative as 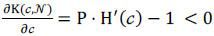. Hence,

In the right hand side inequality above, the first term is negative while the second term is positive. Here, N ⋅ G(c(N)) is the expected number of contestants conducting research at t = 1, when they are using the equilibrium strategy. Note that 1/{N ⋅ G(c)} is the probability of winning the contest for a contestant, which is decreasing in N. Thus, the first term captures the effort-reducing effect of increasing number of contestants in the pool.

On the other hand, the second term incorporates the effort-inducing effect from the competition, as (1 − G(c)))^N−1/N is the probability of winning the contest if a contestant chooses not to conduct research. With more participants in the pool, a contestant without research has less chance of winning the prize, which stimulates it to conduct research in order to be the winner. Clearly, the total effect from the competition is ambiguous. However, if the number of firms gets larger, the effortinducing effect from competition is dominated by the effort-reducing effect. We can use the following result to verify that.

PROPOSITION 3 There exists 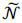< ∞ such that 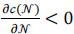, for all N ≥ .

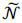PROOF: Here, we get

.

Now {1 − N ⋅ ln (1 − G(c))} ⋅ (1 − G(c))^{N − 1} is decreasing in N and converges to 02. Then, we can find 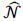which satisfies

.

Finally, set 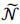= max{2, 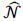} and we get the desired result. ∎

Although the above lemma states that the individual effort level decreases eventually as N increases, it can be increasing for small N. 3 This is in sharp contrast to Taylor (1995), in which the research effort by each firm decreases with the number of the contestants. As more firms participate, each firm becomes increasingly reluctant to make a sunken investment since it becomes more pessimistic about its chances of winning. This result depends on the deterministic cost structure in his model. Every firm in his model is assumed to have the same cost level and ex ante known. A similar result can be found in Che and Gale (2003), where an auction is used for the procurement of an innovation. They show that the optimal number of bidder is two when the contestants have deterministic technology in making innovation. Our model demonstrates that the individual effort level can be non-monotonic to the number of contestants when we consider “randomness” in cost to make research. This suggests that more than 2 contestants may be needed to stimulate innovative activity, when we consider uncertainty in research technology. The following examples support this argument.

1) Numerical Examples

∎ Let P = 1, G(c) = c for c ∈ [0, 1] and b = 1. Then, the interior solution of c* is guaranteed as b > P/N. We have K(c, N) as

.

The result is summarized in Table 1. Note that the effort-inducing effect and the effort-reducing effect are canceled out when the number of firms is increased from 2 to 3.

<Table 1>

c(N) With Uniform Distribution

∎ Consider the case where G(c) = 1- exp(-c). Then, we get

,

when P = 1. In Table 2, we can see that the effort-reducing effect of competition is dominated by the effort-inducing effect when the number of firms is changed from 2 to 3. Here, we have 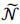= 3.

<Table 2>

c(N) With Exponential Distribution

[Figure 2]

Numerical Examples of Competition Effect

4. Heterogeneity and Innovative Activity

So far, we assumed homogeneity of contestants in the pool. Actually, it is more realistic to consider the heterogeneity of participants. Kaplan et al. (2003) suggest that the cost of an established and well diversified firm is different from that of a smaller competitor. The larger firm already has the necessary infrastructure for the product introduction, while the smaller firm does not have the same capabilities and would find it more costly to innovate. We can incorporate this to our tournament model with different cost distribution.4

We can model this environment in a similar way to our symmetric model. Suppose there are 2 firms in the pool; firm 1 is a strong firm, and firm 2 is a weak firm. Each firm i has G¹(c) as cost distribution, and G²(⋅) first order stochastically dominates the distribution G¹(⋅).This implies that Firm 1 is more likely to get less cost as G²(c) ≤ G¹(c) for every c.

Each firm's threshold level, c^i*, satisfies

,

and

.

From the above equations and by that H(c) = 1/2 when N = 2, we obtain

.

This threshold level of costs is independent of the distribution function. With this result, we get the following Proposition.

PROPOSITION 4 More efficient firm is more likely to make innovation.

PROOF: It is trivial, as G¹(c^1*) ≥ G²(c^2*) when c^1* = c^2*. ∎

This result shows that the sponsor of a tournament will be interested in the efficiency of the participants. In the invitation stage, the sponsor is likely to sort out the inefficient participants to increase the expected value of innovation. So, this is helpful in explaining the behavior of sponsor or the structure of tournaments.