
- P-ISSN 1738-656X


We develop an identity choice model within the context of a stereotyping-cum-signaling framework. The model allows us to explore implications of the fact that, when individuals can choose identity, then the distribution of abilities within distinct identity groups becomes endogenous. This is significant because, when identity is exogenous and if the ability distributions within groups are the same, then inequality of group reputations in equilibrium can only arise if there is a positive feedback between group reputation and individual human capital investment activities (Arrow[1973]; Coate and Loury[1993]). Here we show that when group membership is endogenous then the logic of individuals’ identity choices leads there to be a positive selection of higher ability individuals into the group with a better reputation. This happens because those for whom human-capital-investment is less costly are also those who stand to gain more from joining the favored group. As a result, ability distributions within distinct groups can endogenously diverge, reinforcing incentive-feedbacks. We develop the theoretical framework that can examine the positive selection and the endogenous group formation. The model implies that inequality deriving from stereotyping of endogenously constructed social groups is at least as great as the inequality that can emerge between exogenously given groups.
tereotypes, Statistical Discrimination, Identity Choice, Signaling, 고정관념, 통계적 차별, 정체성 선택, 노동시장 신호
D60, J71, J15
We develop an identity choice model based on a stereotyping-cum-signaling framework. If a worker’s productivity is not perfectly observable, employers have an incentive to use the collective reputations of the identity groups to which job applicants belong in the screening process. A key feature of our model is that individuals belonging to a group with a good collective reputation have a greater incentive to invest in skills than do those who belong to a group with a poor reputation. And yet, given its greater rate of investment in skills, the former group will tend to maintain a better collective reputation than the latter. That is, there can be more than one self-confirming equilibrium in group reputations (Arrow, 1973; Coate and Loury, 1993). Previous work on such statistical discrimination has taken group identity as immutable, so that each individual is affected by the collective reputation of his own group only. We handle the dynamics between the collective reputation and the identity choice problem by relaxing this immutability assumption.
To illustrate the relevance of our model, consider one concrete example—the phenomenon commonly known as “passing.” This widely observed behavior is evidently an instance of identity choice. Talented young members in the group with a worse collective reputation may consider “passing” into the group with a better reputation when the return for such “passing” (e.g., better treatment in the labor market) outweighs its cost (e.g., loss of ties to one’s own kind.) Thus, it has been noted that a significant number of the blacks in the U.S. population consistently passes for White or some other race (Sweet, 2005).1 Moreover, many ethnic Koreans in Japan (most of whom descend from forced laborers in mines and factories who were brought to Japan from the Korean peninsula during the period of Japanese imperialism) are “passing” for native Japanese—by changing both their surnames and their given names when seeking formal employment or marriage. They have done so in order to escape negative stereotypes and prejudices against ethnic Koreans in Japan.2
When passing for a member of the advantaged group with high reputation is not possible due to immutability, the most talented of the stereotyped group are more likely to seek styles of self-presentation that aim to communicate “I’m not one of THEM; I’m one of YOU!” because they are the ones who gain most by separating themselves from the mass (Loury, 2002). Taking the example of the Black population in the US, methods that are known to be used for “partial passing” are: affections of speech, dressing up rather than wearing casual clothes, spending more on conspicuous consumption, and migration to affluent residential areas (Charles et al., 2009; Goffman, 1959). There is evidence that the more educated (or talented) blacks tend to speak standard American English rather than African American English (Grogger, 2011). That is, the most talented of the stereotyped group “pass for” the slightly better-off subgroup that maintains a higher reputation than the stereotyped population as a whole by adopting the cultural traits of the subgroup.
This selective out-migration to the better-off subgroup may undermine solidarity in the disadvantaged population and cause conflict among them, such as the accusation of “Acting White” against the ones who practice the “partial passing” methods (Fryer and Torelli, 2010). However, there might be a social gain through this practice: at least some cultural subgroups of the stereotyped population might be able to recover their reputation when the talented young members gather around certain cultural traits. The usage of the observable cultural traits in the screening process can to some extent cure the social inefficiency caused by imperfect information about the true characteristics of workers.
It is not only backward or disadvantaged groups whose behavior is captured by our model. The emergence of an elite social group out of a population can also be explained through identity choice behavior. Fang (2001) discussed the use of cultural instruments that are intrinsically irrelevant for productivity to form an elite group. He notes that this may help to an account for the complexity of elite etiquette in European (or Confucian) societies, as well as for the greater respect afforded to those with an “Oxford Accent.” Skilled and unskilled workers have different incentives to join a group with unique cultural traits that are expensive to obtain. Thus, the cultural group is treated preferentially by employers due to the higher fraction of skilled workers, even though the cultural traits of the group are not relevant for productivity. We may see an autonomously growing elite subgroup with differentiated cultural traits whose members are considered as distinguished from their peers.
The identity choice model in this paper starts with a standard statistical discrimination framework (Coate and Loury, 1993). We identify multiple self-confirming prior beliefs, which we call Phenotypic Stereotyping Equilibria (PSE). This multiplicity of phenotypic equilibrium explains inequality of collective reputations between exogenous and equally endowed identity groups as being due to positive feedback between a group’s reputation and its members’ investment incentives. But it entails no selection into or out of the groups. However, when membership is endogenous and if the groups’ reputations were to differ in equilibrium, then not only will members of a favored group face greater incentives to invest in human capital. It is also the case that the better-regarded group will, in equilibrium, come to consist disproportionately of high ability/low human capital investment cost types. These are the types who gain most from joining a favored group. The result is that human capital cost distributions between groups endogenously diverge, which reinforces incentive-feedbacks. We call such a group-disparate equilibrium with positive selection a (non-trivial) Affective Stereotyping Equilibrium (ASE).
For the development of our theoretical model, we introduce two affects (i.e., possible group identities), A and B. We assume that the cost to choose affect A rather than B varies across the population. Agents choose affect A if and only if the anticipated return exceeds the agent’s cost of choosing affect A. We further assume that the cost distribution among agents for this affect choice is statistically independent of the cost distribution of human capital investment. (That is, a person’s identity orientation cannot be used to predict their economic abilities.) Nevertheless, we show that in the model’s equilibrium the more able individuals—those with lower human capital investment costs—will tend to choose affect A whenever the collective reputation of the affect A group is better than that of the affect B group. But, of course, their behaving in this way is what causes group A to have a better reputation in the first place!
The main result which we demonstrate with this model is the following: group inequality that derives from the ascriptive stereotyping of endogenously constructed social groups is at least as great as the group inequality that can emerge from the phenotypic stereotyping of exogenously given groups. Again, this is due to the fact that when groups are endogenous then low human capital cost types are disproportionately drawn to the group with a better reputation, causing a skill disparity between groups to endogenously diverge, thereby justifying the disparity of group reputations. The model also implies that there exist multiple (non-trivial) Affective Stereotyping Equilibria whenever multiple Phenotypic Stereotyping Equilibria can be constructed in the labor market structure.
The paper is organized into the following sections. Section 2 develops the model with the identify choice and skill investments. Section 3 defines Phenotypic and Affective Stereotyping Equilibria. Section 4 discusses the implications of the developed model and Section 5 concludes.
In this section, we display the general framework of the model that includes agents’ decision making and the payoff structure. The workers make an investment decision on skill acquisition and choose the identity type before they enter the labor market. Employers set the wage for each worker to be proportional to the worker’s expected productivity using both the productivity-related noisy signal and the identity type. The workers’ decision makings, the employers’ wage setting and the consequent expected payoff are discussed below.
Workers’ Affective/Expressive Behavior: Agents choose affect i ∈ {A, B}. The cost to choose the affect A is k ∈ R. k can be negative: the affect A can generate benefits for some agents. CDF of the affective behavior cost is denoted by H(k). We assume the affective symmetry: H(k) = 1 − H(−k). Agents choose the affect A if and only if the anticipated return exceeds the agent’s cost k. Otherwise, they choose the affect B. WLOG, it is natural to assume that PDF of the cost k, h(k), has one peak at k=0:ℎ'(k)>0 for any k∈(−∞, 0) and ℎ'(k)< 0 for any k∈(0, ∞).3
Workers’ Skill Acquisition Behavior: Agents choose whether to be skilled or not: e∈{0, 1}. The cost to be skilled is c, which is non-negative. CDF of the skill acquisition cost is G(c), in which G(0)≥0 and G(∞)=1.4 WLOG, it is natural to assume that PDF of the cost c, g(c), has one peak at 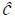 : g'(c)>0 for any c∈(0,
: g'(c)>0 for any c∈(0, 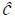 ) and g'(c)<0 for any c∈(
) and g'(c)<0 for any c∈(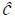 , ∞). An agent chooses (e=1) if the return from doing so exceeds that agent’s cost for the skill acquisition
(c). We impose that c and k are independently distributed.
, ∞). An agent chooses (e=1) if the return from doing so exceeds that agent’s cost for the skill acquisition
(c). We impose that c and k are independently distributed.
Employers’ Wage-setting Behavior: Skill e is not fully identified. Employers observe group identity and noisy signal t ∈ R+ distributed conditional on e. PDF of the signal conditional on e is fe(t) and its CDF is Fe(t). Let us define the function f(π, t) as f(π,t) ≡ πf1(t) + (1 − π)f0(t), which indicates the distribution of signal t of agents belonging to a group of which the skill level(the fraction of the skilled
workers) is believed to be π. WLOG, we assume that 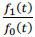 increases with respect to t, which is denoted by MLRP: Monotonic Likelihood Ratio Property. The employers’ belief
that an agent with signal t is skilled is
increases with respect to t, which is denoted by MLRP: Monotonic Likelihood Ratio Property. The employers’ belief
that an agent with signal t is skilled is  . Under MLRP, ρ(π, t) increases with both π and t. The productivity of a skilled worker is ω and that of an unskilled worker is zero. We assume that the wage is proportional
to the expected skill level:
. Under MLRP, ρ(π, t) increases with both π and t. The productivity of a skilled worker is ω and that of an unskilled worker is zero. We assume that the wage is proportional
to the expected skill level:
Workers’ Payoffs: The expected wage from acquiring skill level e is denoted by Ve(π):
in which 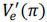 is positive for any e ∈{0,1}. Workers’ expected return acquiring human capital (R(π)) is defined as
is positive for any e ∈{0,1}. Workers’ expected return acquiring human capital (R(π)) is defined as
R(π) is expressed as
The followings can be easily seen
Thus, R(π) is concave and R(0)= R(1)=0, which implies that limπ→0 R' (π)>0 and limπ→1 R' (π)<0. Let us denote argm ax {R(π)} by 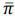 : R'(
: R'(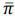 ) = 0.
) = 0.
The first derivatives of V0(π) and V1(π) are
Note that 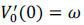 and
and 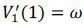 . Since we know R'(0) > 0 and R'(1) < 0, we have
. Since we know R'(0) > 0 and R'(1) < 0, we have 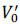 (1) > ω and
(1) > ω and 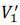 (1) > ω. It is more likely that
(1) > ω. It is more likely that 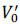 (π) tends to increase as π increases and
(π) tends to increase as π increases and 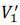 (π) tends to decrease as π increases.
(π) tends to decrease as π increases.
Thus, a worker with cost c, in a group believed to be investing at rate π has the payoff:
in which the function U(π, c) is increasing in π(∵ 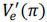 > 0,
> 0, 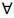 e ∈ {0, 1}) and non-increasing in c.
e ∈ {0, 1}) and non-increasing in c.
In this section, we define the Phenotypic and Affective Stereotyping Equilibria and search for the properties of the equilibria.
Given the employers’ prior belief (π) about human capital investment rate in a population, the fraction of workers who
choose (e=1) is G(R(π)). Let us denote an equilibrium belief/investment rate by  ∈ [0, 1]:
∈ [0, 1]:  = G(R(
= G(R( )). The set of all such equilibria is denoted by ΩCL (Coate and Loury, 1993). Let us call them Phenotypic Stereotyping Equilibria (PSE). Inequality of collective
reputation between exogenous groups in equilibrium is due to feedback between group
reputation and individual investment activities. The individuals in a group with a
better collective reputation have a greater incentive to invest in skills, and with
their greater skill investment rate, the group maintains a better collective reputation,
(and Vice Versa).
)). The set of all such equilibria is denoted by ΩCL (Coate and Loury, 1993). Let us call them Phenotypic Stereotyping Equilibria (PSE). Inequality of collective
reputation between exogenous groups in equilibrium is due to feedback between group
reputation and individual investment activities. The individuals in a group with a
better collective reputation have a greater incentive to invest in skills, and with
their greater skill investment rate, the group maintains a better collective reputation,
(and Vice Versa).
It is most likely that there exists either one or three equilibria in the economy,
because G(c) is S-shaped as displayed in Figure 1. Multiple equilibria  ∈ ΩCL create possibility of Phenotypic Stereotyping (PS) wherein groups are exogenously
and visibly distinct, though equally well endowed. Nevertheless, they fare unequally
in the equilibrium (Panel B of Figure 1).
∈ ΩCL create possibility of Phenotypic Stereotyping (PS) wherein groups are exogenously
and visibly distinct, though equally well endowed. Nevertheless, they fare unequally
in the equilibrium (Panel B of Figure 1).
It is clear that the socially optimal level of human capital investment is G(ω). However, human capital investment is socially inadequate in any PSE  : G(R(
: G(R( )) < G(ω) for any
)) < G(ω) for any  ∈ ΩCL, because R(
∈ ΩCL, because R( ) < ω as
) < ω as 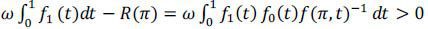 . This implies the social optimality can be further improved through the relaxation
of the given constraints.
. This implies the social optimality can be further improved through the relaxation
of the given constraints.
Absent affective discrimination, workers choose ‘affect’ based on their “natural” orientation: i = B if k>0 and i = A if k <0. This implies that the human capital cost distribution, namely G(c), is the same for both affective groups. Refer to Figure 2 for the case with affective discrimination absent. However, when affective discrimination prevails in the labor market and group membership is endogenous, this is not true any more. Given that the initial reputations of the two affective groups differ, the favored group not only faces great human capital investment incentives, but it also consists disproportionately of low human capital investment cost types, who gain more from joining a favored group. Thereby, it will cause human capital cost distributions between groups to endogenously diverge, reinforcing incentive-feedbacks.
The economic analysis of the story can be developed in the following way. Let πi be employer belief about human capital investment rate in affective group i. Consider two affective groups A and B. Let us define a function ∆U(πA, πB; c) as the payoff difference between a A-type worker and a B-type worker given their skill acquisition cost level c: ∆U(πA, πB; c) ≡ U(πA, c) − U(πB,; c) . Given πA > πB, ∆U(πA, πB; c) is positive because ∂U(π, c)/∂π > 0 . Note that ∆U(πA, πB; c) = −∆U(πB, πA; c) and ∆U(π, π; c) = 0.
An agent with the cost set (c, k) chooses affective behavior i=A if and only if ∆U(πA, πB; c) ≥ k. Otherwise, he chooses affective behavior i=B. Given that c and k are independent, the fraction of agents choosing (i=A) is given by
The fraction of workers choosing (i=A) and (e=1) is given by
Then, the fraction of agents choosing (i=B) is obtained using ΣB = 1 − ΣA and ∆U(πA, πB; c) = − ∆U(πB, πA; c):
Consequently, the fraction of workers choosing (i=B) and (e=1) is given by
Given the employer belief about human capital investment rates (πA, πB), the actual investment rates for the affective groups denoted by ϕ(πA, πB) and ϕ(πB, πA) are
It is noteworthy that when employers’ belief is the same for both affective groups (πA = πB), ∆U(πB, πA; c) is zero and we have R(πA) = R(πB). This implies that the affective behavior does not affect the human capital investment activities: ϕ(πA, πB)= ϕ(πB, πA)(= G(R(πA))).
An equilibrium with affective stereotyping (ASE) is defined as a pair of investment
rates for the affective groups (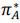 ,
, 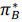 ) ∈ [0, 1]2 such that
) ∈ [0, 1]2 such that 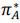 = ϕ(
= ϕ(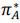 ,
, 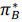 ) and
) and 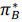 = ϕ(
= ϕ(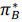 ,
, 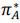 ). The set of all such equilibria is denoted by ΩKL. Note that every PSE corresponds to trivial ASE where differences in affect are uninformative:
(
). The set of all such equilibria is denoted by ΩKL. Note that every PSE corresponds to trivial ASE where differences in affect are uninformative:
(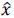 ,
, 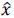 ) ∈ ΩKL if
) ∈ ΩKL if 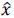 ∈ ΩCL because ϕ(
∈ ΩCL because ϕ(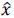 ,
, 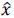 ) = G(R(
) = G(R( )) =
)) = 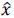 . Affective stereotyping discrimination occurs if and only if
. Affective stereotyping discrimination occurs if and only if 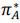 ≠
≠ 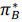 .
.
Note that ∆U(πA, πB; c) can be expressed by
Using R(πA) and R(πB) , we have the following lemma concerning ∆U(πA, πB; c):
Lemma 1. For any c ≤ m ṅ {R(πA), R(πB)}, ∆U(πA, πB; c) = V1(πA)−V1(πB). For any c ≥ m ax{R(πA), R(πB)}, ∆U(πA, πB; c) = V0(πA)−V0(πB). For any c such that m ṅ {R(πA), R(πB)} < c < m ax {R(πA), (πB)}, we have
The above lemma is summarized in Figure 3. Panel A of the figure displays the case with πA > πB and panel B does the case with πA < πB. It is easily seen that ∆U(πA, πB; c) > 0 for any c if and only if πA > πB. Therefore, we have the following result.
Proposition 1. When employers have different beliefs about two affective groups (πA ≠ πB), the number of workers who adopt the ‘affect’ corresponding to the favored employers’ belief is greater than that of workers who adopt the ‘affect’ with the less favored employers’ belief: Σi > Σj if πi > πj for any i,j ∈ {A, B}.
That is, in the current setting with symmetric cost distribution, more than half workers adopt the ‘affect’ that corresponds to the more favorable employers’ belief: Σi > .5 and Σj < .5 if πi > πj for any i, j ∈ {A, B}. The Lemma 1 implies that ∆U(πA, πB; c) is non-increasing with respect to c whenever R(πA) > R(πB), and non-decreasing whenever R(πB) > R(πA). It leads to the following useful lemma.
Lemma 2. Whenever R(πA) > R(πB), the following holds: ϕ(πA, πB) > ϕ(πA, πA) and ϕ(πB, πA) < ϕ(πB, πB). In a symmetric way, whenever R(πA) < R(πB), the following holds: ϕ(πA, πB) < ϕ(πA, πA) and ϕ(πB, πA) > ϕ(πB, πB). Even when πA ≠ πB, the following holds if R(πA) = R(πB): ϕ(πA, πB) = ϕ(πB, πA) = ϕ(πA, πA) = ϕ(πB, πB)
The above lemma implies the following proposition.
Proposition 2. The disproportionately more talented workers, whose human capital investment costs (c) are relatively lower, choose the ‘affect’ that corresponds to the greater return to human capital investment: given R(i) > R(j), ϕ(i, j) > G(R(i)) and ϕ(j, i) < G(R(j)) for any i, j ∈ {πA, πB}.
Ⅳ. Implications and Further Discussion
It is obvious that (x, x) is an affective stereotyping equilibrium for any phenotypic stereotyping equilibrium x because x = ϕ(x, x). These ASE are called trivial ASE in this paper. We are more concerned with the non-trivial ASE in which the affective group’s reputations differ in equilibria: x≠y. Intuitively, we can say that the existence of non-trivial ASE is guaranteed given the multiple PSE. Suppose that there exist three PSE (πh, πm, πl) in the given labor market structure as displayed in Panel B of Figure 1. Imagine that an affective group’s reputation is the level of πh and the other affective group’s reputation is that of πl. Note that the following must be true given the multiple PSE: R(πh)>R(πl). Then, the combination (πh, πl) cannot be stable because of Proposition 2: given R(πh)>R(πl), φ(πh, πl)>G(R(πh)) and ϕ(πl, πh)<G(R(πl)). That is, the skill investment rate of the entering cohort to the affective group with πh is greater than the current skill level of the group G(R(πh)), while that of the entering cohort to the other affective group with πl is smaller than the current skill level of that group G(R(πl)). The situation is well described in Panel A of Figure 3. Therefore, there must be at least two non-trivial ASE: one can emerge out of the initial combination (πh, πl) and the other out of the initial combination (πl, πh).
We also know that the skill difference between two entering cohorts (ϕ(πh, πl) − ϕ(πl, πh)) is greater than that between the two groups’ current skill levels (πh − πl). This implies that the inequality between endogenous groups in some non-trivial ASE can be greater than inequality between exogenous groups in any PSE.
Finally, to see how our model can be used to shed light on labor market phenomena other than ethnic/racial group inequality, let us consider the problem of “re-branding ex-cons.” The main feature of the labor market for ex-convicts is that employers wish to avoid associating with those who end up returning to criminal activity, but employers cannot be certain from information which among the convicts will and which will not do so. However, the convicts themselves are presumed to know their own intentions. Under this informational asymmetry, employers choose not to hire any ex-cons leaving all of them unemployed.
Let us imagine a re-branding program run by the government along the following line: There is to be a certifiable and costly activity such that, before going into the labor market, ex-cons can elect to join this program or not. Those who will go straight are more willing to join the program than those who will return to crime because those going straight have greater gain from having a job in the market. The collective reputation of the ex-con subgroup with the program certificate improves with the greater fraction of ex-cons going straight joining the program, so that those with the program certificate will be hired and those without it will not be hired by employers in the labor market. That is, notwithstanding the informational asymmetry and the adverse selection issue in the market, a government can nevertheless design a costly program by means of which some ex-cons can credibly convey their good intentions to employers. The social efficiency can be achieved by the introduction of the costly program.
In this paper, we develop an identity choice model that can explain social activities such as passing and selective out-migration from a stereotyped group, loosening the assumption of group identity immutability in standard statistical discrimination models. More talented members with low human capital investment cost have a greater incentive to identify themselves with a group that has a better collective reputation. The positive selection into a favored group plays a critical role in causing human capital cost distributions between groups to endogenously diverge. This model can be applied to many other social settings such as code switching (Goffman, 1959) and generating certificates to fight against negative stereotypes (e.g. re-branding ex-cons).
The National Longitudinal Survey conducted by the Department of Labor of the US shows that 1.87 percent of those who had originally answered “Black” to the interviewer’s race question in 1979 switched to either “White,” “I don’t know, ” or “other,” by 1998.
Every year about 10,000 Koreans living in Japan, out of around 600,000 Korean descendants holding Korean nationality, choose to be naturalized, giving up their names and original nationality (Fukuoka et al., 1998).
, , , & . (2009). Conspicuous Consumption and Race. The Quarterly Journal of Economics, 124, 425-467, https://doi.org/10.1162/qjec.2009.124.2.425.
, & . (2010). An Empirical Analysis of ‘Acting White’. Journal of Public Economics, 94, 380-396, https://doi.org/10.1016/j.jpubeco.2009.10.011.