
- P-ISSN 2586-2995
- E-ISSN 2586-4130


Based on a quantitative, heterogeneous agent general equilibrium model, we compute the optimal tax rates for labor and capital incomes for the Korean economy. According to our model, a more progressive income tax schedule along with a higher capital tax rate can increase average welfare by as much as 0.86% of permanent consumption. Approximately 64% of house-holds, those with low assets and low productivity, are better off when a more progressive optimal tax schedule is adopted. Despite the potentially significant welfare gains, our calculation should be interpreted with caution because our benchmark model does not take into account possible capital outflows or the increased administrative costs associated with high taxes.
Inequality, Korean Economy, Optimal Income Taxes, Progressivity Capital Tax
E25, E62, H21
Among OECD members, Korea is considered a “low-inequality and low-redistribution” country. Figure 1 plots the before- and after-tax/transfer income Gini coefficients for 31 OECD countries. All 31 countries are located below the 45-degree line, indicating that in all countries incomes are redistributed from the rich to the poor. In terms of before-tax/transfer incomes, the Gini coefficient of Korea is the lowest (0.34) among the OECD members, whose average is 0.47. In terms of after-tax/transfer incomes, the Gini coefficient of Korea is about the average of the OECD countries (0.31). In terms of percentage changes in the income Gini—the so-called improvement rate of income inequality after taxes and transfer Korea exhibits only a 9% decrease, whereas the average decrease in Gini coefficients among the OECD countries is 35%.
While finding the right degree of income redistribution has always been a primary concern for economists and policy makers, it is not an easy task, since it requires modeling a complicated political process and aggregating individual preferences. A recent development of quantitative general equilibrium models with heterogeneous agents allows us to address this issue at least partially. In this paper, we compute the optimal income tax rates for labor and capital for the Korean economy. We ask the following two questions: (i) What is the labor and capital income tax rates that maximize the average utilitarian welfare of the society? (ii) Who will be better off or worse off from the fiscal reform that adopts the tax rate that maximizes average welfare?
We examine these questions through the lens of the Aiyagari model (1994) augmented with endogenous labor supply (e.g., Pijoan-Mas (2006) and Chang and Kim (2007)). In this model, workers are identical in preferences, but face uninsurable productivity shocks and borrowing constraints. Earnings and wealth distributions emerge as an equilibrium. In the model economy, we introduce three major taxes: total income tax, capital tax, and consumption tax.
Households are liable to a progressive income tax schedule. More specifically, we adopt a parametric net tax function developed by Heathcote, Storesletten, and Violante (2013) (referred to as HSV hereafter) to capture the progressive tax schedule in a simple way. In addition, we allow a separate capital income tax to distinguish the labor and capital income taxes. The consumption tax rate in our model is fixed at the current value-added tax (VAT) rate of 10%.
We calibrate the model economy to match several salient features of the Korean economy. For example, the stochastic process of individual productivity is estimated from the panel data of wages in the Korea Labor Income Panel Study (KLIPS). The cross-sectional income and wealth distributions of the model are somewhat less dispersed than but largely comparable to those in the data.
We then look for the optimal degree of progressivity in the income tax schedule and capital tax rate that maximizes the (equal-weight) utilitarian social welfare function. According to our model, the optimal tax policy requires a more progressive income tax schedule and a higher capital income tax rate than the current one. For example, the marginal tax rate for the household in the 9th decile (top 10%) in the income distribution has to increase from the current 22% to 31%. The average net income tax rate has to fall from the current 3.75% to -0.9%.
When the optimal tax reform is in place, the average welfare of households increases by as much as 0.86% of steady-state consumption, which is approximately 300 thousand won (in 2010 value) each year. About 64% of households will be better off from this optimal tax reform. Households with low assets and low productivity win, but households with high assets or high productivity will lose from the optimal tax reform. Across consumption deciles, households in the 1st consumption decile gain welfare by as much as 3.4% of their permanent consumption (709 thousand won annually). Households in the 9th decile lose welfare by as much as 3.4% of their permanent consumption (1,656 thousand won annually).
Despite a potentially large welfare gain from tax reforms, our results should be interpreted with caution because our benchmark model does not take into account the possible capital outflow or the increased administrative costs associated with high income taxes. Indeed an open-economy version of our model indicates that there will be a significant capital flight from high capital income tax rates. A sizable administrative cost due to bureaucracy would also undermine the potential welfare gain from high taxes.
Our results are closely related to those in the existing literature. Aiyagari and McGrattan (1998) developed a heterogeneous agents model with incomplete markets and analyzed the optimal debt policy under the utilitarian social welfare functions. However, while the income tax schedule is linear in their model, we allow for progressive income taxes. HSV (2014) provided a tractable model of optimal tax progressivity. The endogenous labor supply and skill accumulation limits high progressivity—the optimal rate in their model is lower than the current progressivity. Our model embodies capital tax rates and consumption tax rates as well as income tax and focuses on the optimal tax rate for the Korean economy. Our results imply that the optimal tax rate in Korea is much higher and more progressive than the current tax schedule. Chang et al. (2015) computed the optimal income tax rate for each of the 31 OECD countries, including Korea.1 Under the linear income tax and lump-sum transfer, Chang et al. found that the optimal income tax rate in Korea is 32%, much higher than the current tax to GDP ratio of 23%. In this paper, we extend the model in Chang et al. to incorporate a progressive income tax schedule as well as separate capital and consumption taxes. To our knowledge, this is the first estimate to find the optimal progressivity for the Korean economy based on a quantitative heterogeneous agents general equilibrium model.
The remainder of the paper is organized as follows. Section II documents key statistics about the tax and redistribution policies of Korea and other OECD countries. Section III lays out the benchmark model economy and calibrates to Korean data. In Section IV, we compute the optimal tax reform under the utilitarian social welfare function and examine who will be better off from the optimal tax reform. Section V concludes.
We document some stylized facts about tax and redistribution policies in Korea and the OECD countries. Table 1 summarizes the tax-to-GDP ratios, Gini coefficients, and per capita GDP of 34 OECD countries. The total tax revenue to GDP ratio of Korea is 23%, the third lowest among the OECD countries, whose average is 33%. The second and third columns of Table 1 report the before- and after-tax/transfer income Gini coefficients. (The before-tax income Gini is not available for Turkey, Mexico, and Hungary.) Korea shows the lowest before-tax income Gini (0.34). But, Korea’s after-tax income Gini (0.31) is close to the OECD average. The before-tax income Gini ranges from 0.37 (Switzerland) to 0.59 (Ireland), and the after-tax income Gini from 0.24 (Iceland) to 0.51 (Chile). The fourth column represents the percentage decrease from the before-tax income Gini to after-tax/transfer income Gini coefficients (a measure of the degree of redistribution). In Korea, taxes and transfers reduce income inequality by only 9%, whereas they reduce income inequality by 35% on average among 31 OECD countries. Only Chile (4%) shows a smaller decrease than Korea. These facts imply that Korean currently adopts a “low tax and low transfer policy.”
Source: Wealth Ginis are obtained from Credit Suisse (2012) and others are from the OECD (2015).
Source: Authors’ calculations with data from the OECD (2015) and Credit Suisse (2012).
Two income Ginis are, however, modestly correlated with the correlation coefficient of 0.4, indicating varying degrees of redistribution policies across countries. Tax revenues are closely related to redistributions and after-tax income Ginis. As Figure 2 illustrates, the improvement rates of income Ginis are fairly strongly correlated with the tax to GDP ratios (correlation coefficient of 0.65). This is confirmed by Figure 3, which shows a strong negative correlation, −0.70, between the tax to GDP ratio and the after-tax income Gini. Broadly speaking, high taxes are likely to be used for income redistribution purposes and to make incomes more equal.
Korea’s tax system consists of ten national and eleven local taxes (MOSF 2012). As described in Table 3, national taxes are classified into internal taxes, customs duties, and three earmarked taxes. Local taxes are classified into province taxes and city-county taxes. Table 4 reports the tax revenues (relative to national GDP) of each item. The total tax revenue, including social security contributions, was 23.2% of GDP in 2010 (OECD). Most of the tax revenue comes from individual income taxes (3.3% of GDP), corporate income taxes (3.2%), social security contributions (5.3%), and the value-added tax (4.1%). More detailed information about the major taxes (income taxes, corporation income taxes, and the value-added tax) and social insurance is provided in Appendix A.
Table 5 compares the Korean tax revenue structure to those of the OECD countries. Korea’s total tax revenue (23.2% of GDP) is much smaller than that of other OECD countries (average 32.8%). Only Chile (19.5%) and Mexico (18.5%) show lower tax revenues than Korea. The major tax items are similar across OECD countries; individual income taxes, corporate income taxes, social security contributions and taxes on goods and services. The low tax revenues relative to GDP in Korea are mainly due to the low individual income taxes and social security contributions in Korea. The revenues from individual income taxes and social security contributions are 3.3% and 5.3% of GDP, respectively, in Korea. Corresponding figures for the OECD on average are 8.2% and 8.9%, respectively. Also, taxes on goods and services (7.9% of GDP), including value-added tax revenues, are slightly lower than the OECD average (10.7%). The tax revenue from corporate income (3.2% of GDP) is slightly higher than the OECD average (2.8%).
We now examine the detailed tax burdens across households in Korea. According to the Household Income and Expenditure Survey (HIES), the average household in Korea paid 3.5% of its factor income (total income minus public/private transfers) as taxes and 5.6% of their factor incomes as social security contributions in 2010.
Table 6 reports the taxes and social security contributions across various income deciles. The ratio of taxes and contributions to factor income increases gradually, from 7.4% in the third decile of income distribution to 11.2% in the tenth decile, reflecting the progressivity of taxes. (The increase is not uniform owing to differences in household compositions and received transfers.) Even in the tenth decile, the average tax rate is quite low, despite the top statutory income tax rate (41.8%) and social security contribution (4.5% for pensions and 3.035% for health insurance).2 This may reflect the fact that various deductions lower the effective tax rate considerably, even for those in the high-income brackets. Surprisingly, while the taxes and contributions paid by households in the first decile (the poorest 10%) are the lowest, their taxes with regard to factor incomes are very high (12.4%). One reason is that in the first decile, the average household size (2.4) is much smaller than the population average (3.3); moreover, the average age of household head (59.9) is much older than the population average (48.5). Because many tax deductions are child related, the tax burden on households without young children would be much greater than the population average. To avoid this issue, we next consider tax rates based on household-size equivalent units.
Notes: Factor Income = Labor + Business + Capital Income = Total Income − Transfer (public/private)
Total Burden = (Tax + Pension Contribution + Health Insurance)/Factor Income
Source: Household Income and Expenditure Survey.
Table 7 reports the market income, disposable income, and the net tax rate 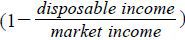 based on the equivalized scale (income divided by the square root of the household
size) across income deciles.3 The net tax rate of households in the first income decile is now much lower (−27%)
than those in other deciles, implying that these households received 27% of their
market income as a net transfer in 2010. HIES also reports the Gini coefficients before
taxes and transfers (shown in Table 8). Taxes and social transfers reduced the income Gini by approximately 9%-10% in the
years 2009-2013.
based on the equivalized scale (income divided by the square root of the household
size) across income deciles.3 The net tax rate of households in the first income decile is now much lower (−27%)
than those in other deciles, implying that these households received 27% of their
market income as a net transfer in 2010. HIES also reports the Gini coefficients before
taxes and transfers (shown in Table 8). Taxes and social transfers reduced the income Gini by approximately 9%-10% in the
years 2009-2013.
Notes: All incomes are equivalized: divided by the square root of household size.
Source: Household Income and Expenditure Survey.
Summarizing the progressivity of taxes is not simple owing to the complexity of the income tax schedule and various deductions. One practical way is to assume a specific parametric form of tax function with a few parameters. We assume that the individual income tax schedule follows the HSV (2014) type (referred to as the HSV tax function hereafter):
In the HSV tax function, two parameters, λ and τ, characterize disposal income, D(yi), as a function of the household’s market income yi.4
We estimate τ and λ based on cross-sectional data. Because tax and transfer data at the individual household level are not available, we use the reported data across income deciles for 2006-2013 as our data points by assuming that the parameters are constant during the sample period. Figure 4 plots the market and disposable incomes at each decile point from 2006 to 2013.5 Note that both market income and disposable income are equivalized by household size; income is divided by the square root of the household size. The log of disposable income (log D(yi)) and the log of market income (log yi) appear to be nearly linear, implying that the HSV tax function captures the progressivity of taxes and transfers in the data quite well. Table 9 reports the estimation results after regressing log D(yi) on log yi.
Notes: Data points are from the equivalized income deciles for 2006 to 2013 (HIES).
Based on this estimated HSV tax function, we can now compute the net tax rates and marginal tax rates across household incomes. Table 10 compares the actual net tax rates in the HIES and those based on the estimated HSV tax function. The estimated tax rates fit relatively well for middle-income families. The net tax rates in the second, fourth, sixth, and eighth deciles are respectively −5.4%, 2.7%, 4.2%, and 6.4% in the HIES. The corresponding rates based on the estimated HSV tax function are −6.7%, 0.0%, 3.7%, and 7.8%. One of the shortcomings of the HSV tax function is its poor approximation at the low-income level. The net tax rate in the first decile in the HIES is −27.0%, whereas the corresponding rate according to the estimated HSV function is −15.7 %.
Our benchmark economy extends Aiyagari’s (1994) model to endogenous labor supply and introduces three taxes: progressive income tax, capital tax, and consumption tax.
Households: There is a continuum (measure one) of worker-households who have identical preferences and face an idiosyncratic productivity shock x , which evolves over time according to a Markov process with a transition probability distribution function πx (x' | x) = Pr(xt+1 ≤ x' | xt = x). When a household with labor productivity xt chooses to work for ht hours, its labor income is wtxtht, where wt is the wage rate for the efficiency unit of labor. Households hold assets at that yield the real rate rt . Both labor and capital incomes are liable to progressive taxes of the HSV tax function (y−λ(y)(1−τ)). Note that the HSV tax functions include transfers as well as taxes. Households are also liable to a consumption tax at the rate τc. A household maximizes its lifetime utility:
subject to
where ct is consumption. Parameters σ and γ represent relative risk aversion and labor-supply elasticity, respectively. Capital markets are incomplete in the sense that physical capital is the only available asset for households to insure against idiosyncratic shocks to their productivity, and households face a borrowing constraint: at ≥ a for all t .
In our model, households that own assets pay capital taxes at the rate τk separately. These capital taxes are intended to capture corporate income taxes in the data. While the corporate income tax is levied on firms’ profit, in our model firms operate in a competitive market yielding zero profits. A perfectly competitive goods market is assumed to avoid a complicated market structure on the production side (see below). Since the assets held by households in our model are the claims on production capital, we interpret the taxes on capital income in our model as a proxy for taxes on stockholders’ incomes in the data. Thus, in our model, individual income taxes (HSV tax function) are levied on household capital incomes (wtxtht + (1−τk)rtat) after paying corporate income taxes. Finally, households differ ex post with respect to their productivity xt and asset holdings at , whose cross-sectional joint distribution is characterized by the probability measure μt(at,xt).
Firms: The representative firm produces output through a constant-returns-to-scale Cobb-Douglas technology using capital, Kt, and effective units of labor, Lt = ∫htxtdμ. Firms invest It and capital depreciates at the rate δ each period:
subject to
Government: Using total tax revenue collected from three types of taxes, the government consumes the goods G and transfers the rest of the revenue to households as a lump-sum transfer. The government also balances its budget every period:
where T(yt) = wtxtht + (1 − τk)rtat − λ(wtxtht + (1 − τk)rtat)1−τ
Recursive Representation: It is useful to consider a recursive equilibrium. Let V( a, x ) denote the value function of a household with asset holdings a and productivity x . Then V can be expressed as follows:
subject to
Equilibrium: A stationary equilibrium consists of a value function, V(a,x); a set of decision rules for consumption, asset holdings, and labor supply, c(a,x) , a'(a,x) , h(a,x) ; aggregate inputs, K , L ; and the invariant distribution of households, μ(a,x), such that:
1. Individual households optimize: Given w and r , the individual decision rules c(a,x), a'(a,x), h(a,x) and V(a,x) solve the Bellman equation.
2. The representative firm maximizes profits:
3. The goods market clears:
4. The factor markets clear:
5. The government balances the budget:
6. Individual and aggregate behaviors are consistent:
For all A0 ⊂ 𝒜 and X0 ⊂ 𝑋 ,
The time unit is one year. Workers are not allowed to borrow; a = 0. The labor income share α is 0.64, and the annual depreciation rate of capital δ is 10%. The labor-supply elasticity γ is set to 1. The risk-aversion parameter σ , 1.4, is obtained from Chang et al. (2015). The discount factor β = 0.939 is set so that the real interest rate is 6%6 The disutility for labor B = 6.126 is chosen to match average working hours, 0.398. 7 The stochastic process for the idiosyncratic productivity shock is assumed to be an AR(1): xt = ρxxt−1 + εt where εt ∈ N(0,σx). We use the values in Chang and Kim (2008), who estimated them from the panel data of individual wages in the KLIPS data. The estimates are ρx = 0.8 and σx = 0.354.
The consumption tax rate, τc, is set to the current VAT rate of 10%. The consumption tax revenue in our model is 6.5% of GDP, which is somewhat smaller than the tax revenue on goods and services, 7.9% of GDP in the data (OECD 2010). The capital tax rate τk, is set to 24%, so that the capital tax revenue (relative to output) in the model is the same as tax revenue on corporate income in the data (3.2% of GDP). The parameter for the tax progressivity τ = 0.14 is obtained from our estimate based on the HIES. The parameter for the average level of taxation λ= 0.90 is chosen so that the average net income tax rate in our model is the same as that in the HIES (3.75%). Government consumption, G, is determined by the balanced budget. The government consumption to GDP ratio in our model (12.5%) is slightly smaller that that in the data (13.5% according to the National Income Account 2010).
The before- and after-tax/transfer income Gini coefficients are 0.341 and 0.310, respectively, in the HIES (2010) and 0.390 and 0.357, respectively, according to the Survey of Household Finance and Living Conditions (SHFLC 2011).8 The income Gini coefficients in our model (0.366 and 0.318, respectively, for before and after tax) fall between those from the HIES and the SHFLC. Table 12 compares the income and wealth shares across quintile groups of the income distribution between the model and the data. The top 20% (the 5th quintile) of households earn 37.3% and 46.4% of total disposable incomes in the HIES and the SHFLC, respectively. The corresponding number in our model is 40.2%. The HIES reports that households in the 1st, 2nd, 3rd, and 4th quintiles earn 6.6%, 13.6%, 18.4%, and 24.0% of total disposable income. The corresponding shares are 3.8%, 9.7%, 16.0%, and 24.2% in the SHFLC. Those in our model are 8.1%, 12.4%, 16.6%, and 22.7%.
Source: Household Income and Expenditure Survey (HIES 2010), Survey of Household Finance and Living Conditions (SHFLC 2010).
The wealth Gini coefficient for Korea is 0.628 according to the SHFLC (2010), whereas it is 0.545 in our model.9 Table 12 also reports the quintile groups of the wealth distribution. The SHFLC found that households in the 1st, 2nd, 3rd, and 4th quintiles own 0.4%, 4.7%, 10.6%, 20.4%, and 64.0% of total assets, respectively. The corresponding shares in our model economy are 0.7%, 5.4%, 13.4%, 25.7% and 54.8%, respectively. Income and wealth inequality in our model is higher than that in the HIES, but lower than that in the SHFLC. Overall, the income and wealth distributions in our model economy resemble those from the data quite well.
Table 13 compares the major variables in the data to those in our model. The consumption tax revenue and government consumption in our model are close to those in the data, although we did not target those ratios. Tax revenues on goods and services were 7.9% of GDP (OECD 2013) in 2010; the corresponding rate in our model is 6.5%. Government consumption (13.5% of GDP in 2010) in the National Account (OECD 2014) is similar to that (12.5%) in our model.
Source: Household Income and Expenditure Survey (HIES), Survey of Household Finance and Living Conditions (SHFLC), OECD database
According to our calibration strategy, the model economy matches the average net tax rate in the HIES (3.75%). Table 14 compares net and marginal tax rates at decile points between the model and the data. The net tax rate of households in the 1st decile (bottom 10%) is −27.0% in the HIES, and −15.7% according to the estimated HSV tax function. The corresponding figure in our model is −13.9%. The net tax rate in the 9th decile in the HIES is 7.0%, somewhat lower than that in our model (9.5%). The marginal tax rates in the 1st and 9th deciles under the estimated HSV tax function (0.2% and 22.8%) are similar to those in our model (1.7% and 21.9%). In the middle deciles, the marginal tax rates under the estimated HSV tax function (7.9%, 13.7%, 16.9% and 20.4%) are slightly higher than those in our model (5.1%, 9.5%, 13.8%, and 18.4%). Overall, the marginal tax rates in our model approximate those under the estimated HSV fairly well except for the 1st decile (the bottom 10%) despite a simple parametric functional form.
Notes: All incomes are equivalized income at decile points in 2010. Marginal tax rates are based on the estimated HSV tax function. The relative incomes are relative to the population average.
In order to compare the gross tax rates in our model, we need further assumptions about the transfer because the HSV tax function is defined in terms of net taxes. We assume a lump-sum transfer to all households. In fact, the amount of transfer is actually pretty close to lump-sum in the HIES. The average transfers (public plus private, unequivalized income) are 323,309 won in the HIES (2010), while the average transfers in the 1st and 10th deciles are 341,708 and 372,828.
More specifically, we look for the amount of lump-sum transfer in our model so that the individual income tax to output ratio matches that in the data (income tax and social security contributions to GDP ratio of 8.6%, according to the OECD Tax Revenues 2010). Table 15 compares the average gross tax rates across various income deciles. The gross tax rates in our model resemble those in the HIES well except for the top end of the distribution. The gross tax rate of 11.2% in the 10th decile in the HIES is much lower than that in our model, 17.4%.
Notes: Tax rates in the HIES are the same as those in Table 6; income is not equivalized, and tax rates are taxes and contributions divided by factor income.
C. Optimal Tax Reform
In the previous section, we developed a quantitative model that approximates income inequality and tax policies in Korea. We now address the following questions using this model economy: (i) What is the optimal tax rate that maximizes the utilitarian social welfare function? (ii) Who will be better (or worse) off from the fiscal reform to adopt the optimal tax rate?
One of the most important subjects in public finance is to characterize the optimal tax policy. This task often requires appropriately aggregating individual preferences, which is challenging and controversial. A common practice is to use a social welfare function that averages the utility of the population with equal weights (i.e., utilitarian criteria). In the context of our model, the utilitarian social welfare function can be written as:10, 11
where V(a0, x0 ; τ, τk) is the discounted sum of the lifetime utility of a household with asset holdings a0 and productivity x0, and μ(a0, x0 ; τ, τk) is the distribution of households over (a0, x0) in the steady state given tax progressivity τ and a capital tax rate τk, i.e.,
We assume that the model economy is at its steady state under the current tax progressivity
(τ) and two tax rates (τk, τc) as reported in Table 13. We then look for the new combination of tax progressivity τ*, and capital tax rate, 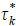 , that maximizes W(τ, τk*), including the welfare of households during the transition period to the new steady
state.12 We assume that the consumption tax rat τc is fixed at 0.1. We also assume that the government consumption to output ratio G/Y is held constant. The average level of taxation λ, is determined to ensure a balanced budget every period.
, that maximizes W(τ, τk*), including the welfare of households during the transition period to the new steady
state.12 We assume that the consumption tax rat τc is fixed at 0.1. We also assume that the government consumption to output ratio G/Y is held constant. The average level of taxation λ, is determined to ensure a balanced budget every period.
We will compute the social welfare gains under the new tax progressivity (τ) and capital tax rates (τk). The welfare gain in consumption-equivalence units, Δ, is defined as:
where c0, h0, μ0 are initial steady states and c1, h1, μ1 are those after the reform (including transitions).
Table 16 reports the welfare gains under various tax reforms. Out of 20 combinations we consider
around the current values, τ* = 0.24 and 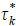 = 0.39 achieve the largest welfare gain—a 0.86% increase in permanent consumption.
When converted into 2010 wons, the consumption of all households increases by 300
thousand won every year.13 Table 17 shows the net and marginal income tax rates under the new steady states.14 The average net tax rates of income decreases from 3.75% to −0.87% on average due
to a more aggressive redistribution. With the increased progressivity, households,
except for those in top 10% income distribution, now face lower net tax rates. The
marginal tax rates increase with income at a steeper rate. The marginal tax rate of
31.1% in the 9th decile in the new steady state is much higher than 21.9% under the
initial steady state. Since the HSV function is defined in terms of net tax burden,
we need another assumption in order to determine the gross tax rates across income
levels. We assume that the gross tax rate of households at the 2nd decile is fixed
in all tax reforms we consider.15 Table 17 reports the gross tax rates at various decile points under the optimal tax function.
The gross tax rates of low-income households change little after tax reform. But those
of high-income households increase considerably. For example, the gross tax rate in
the 9th decile increases from 13.7% to 17.9%.
= 0.39 achieve the largest welfare gain—a 0.86% increase in permanent consumption.
When converted into 2010 wons, the consumption of all households increases by 300
thousand won every year.13 Table 17 shows the net and marginal income tax rates under the new steady states.14 The average net tax rates of income decreases from 3.75% to −0.87% on average due
to a more aggressive redistribution. With the increased progressivity, households,
except for those in top 10% income distribution, now face lower net tax rates. The
marginal tax rates increase with income at a steeper rate. The marginal tax rate of
31.1% in the 9th decile in the new steady state is much higher than 21.9% under the
initial steady state. Since the HSV function is defined in terms of net tax burden,
we need another assumption in order to determine the gross tax rates across income
levels. We assume that the gross tax rate of households at the 2nd decile is fixed
in all tax reforms we consider.15 Table 17 reports the gross tax rates at various decile points under the optimal tax function.
The gross tax rates of low-income households change little after tax reform. But those
of high-income households increase considerably. For example, the gross tax rate in
the 9th decile increases from 13.7% to 17.9%.
Notes: All numbers are % change (consumption equivalent) from the current steady state.
Table 18 compares the current steady state and the new steady state under optimal tax reform. The Gini coefficient before tax and transfers (0.356) under optimal tax reform is slightly lower than the current one (0.366). However, the Gini coefficient after tax and transfers decreases from 0.318 to 0.274 after reform. As a result, taxes and transfers reduce the Gini coefficient by 23% under optimal tax reform, which is 13.2% in the current steady state. The tax reform has little effect on wealth distribution; the new wealth Gini (0.536) is similar to the current one (0.545). Since high tax rates lower after-tax returns on capital, and more social transfers weaken the insurance motive under tax reform, individual savings decrease drastically and the interest rate rises. The capital stock after tax reform is 77% of current steady state, and the corresponding interest rate is now 8.4% (the current rate is 6%). On the contrary, both wage and working hours fall in the new steady state. Low capital stock and labor supply reduce total output by 12%. Aggregate consumption also decreases, but not as much as output. Increases in tax progressivity raise tax revenues on income. However, social transfers increase more than income tax and the net tax rate decreases. Tax revenues on capital income increase from 3.2% in the current steady state to 6.3% in the new steady state.
Figure 5 demonstrates the transition paths from the current to the new steady state under optimal tax reform. All values are relative to the current steady-state level, which is set to 100. Output drops sharply as soon as the new tax reform is in place, and then decreases gradually. Since households reduce savings, aggregate capital falls continuously. Aggregate consumption rises slightly in the beginning as accumulated capital is spent, but goes below the current level in the long run. Working hours drop in the beginning and remain low. The interest rate, which falls in the beginning, keeps rising to 40% higher than the current rate. On the contrary, wages increase in the beginning and then falls.
Note: All values are relative to the current steady state, which is normalized to 100.
We now calculate how many households are better off from each tax reform. In computing
welfare under tax reform, we include welfare during the transition to the new steady
state. Table 19 reports the fraction of households (%) that are better off from each tax reform.
Under optimal tax reform ( τ* = 0.24, 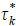 = 0.39), about 64% of households are better off. If we assume that voting is binary
between the current and the new tax scheme, 64% of households will support optimal
tax reform.
= 0.39), about 64% of households are better off. If we assume that voting is binary
between the current and the new tax scheme, 64% of households will support optimal
tax reform.
Figure 6 illustrates the asset and productivity levels at which households are indifferent between the optimal tax reform and the status quo. For comparison with the actual data, we convert the units in our model to 2010 wons (by matching average income in our model to that in the 2010 HIES). Average working hours in our model, 0.398, is also set to the average annual working hours 2,187 in Korea (OECD 2010). In Figure 6 households below the dotted line are better off with the optimal tax reform. Clearly, households with low asset and low productivity win from tax reform. (The vertical and horizontal lines in Figure 6 represent the average and ± one standard deviation of assets and individual productivity.16)
Note: Assets and wages are rescaled so that average income in the model matches that in the data.
We also report the welfare gains at various consumption deciles under optimal tax reform in Table 20. The welfare gains of a particular household i, Δi, in consumption-equivalence units is:
where ci0, hi0 are the initial steady states and ci1, hi1 are those after reform (including transitions) for each individual i . Household in the 1st consumption decile gain 3.4% in terms of permanent consumption. Households in the 2nd, 4th, 6th deciles also gain welfare. However, households in the 8th and 9th deciles lose welfare by as much as 1.4% and 3.4% of their permanent consumption, respectively. When converted into 2010 won units, households in the 1st decile gain 709 thousand won and those in the 9th decile lose 1,656 thousand won.
In our benchmark model, we assume that there is no administrative cost associated with collecting taxes and transferring resources (or cost associated with bureaucracy). However, collecting tax revenues as well as transferring incomes may require costs. In this section, we introduce some administrative costs of government.
While it is difficult to measure the cost of bureaucracy, according to the OECD, the cost of collection ratio (administrative costs/net revenues) among 32 OECD countries was 1.1% on average in 2010.17 In the same report, the cost ratio in Korea was 0.81%. Eurostat reports the structure of social protection expenditure among 28 EU countries. Administrative costs account for 3.0% of total expenditure in 2012.18 Based on these numbers, we now assume that the administrative cost is 4% of total transfers (1% for collecting taxes and 3% for transferring). As a result, total government expenditure becomes G + 0.04 TR where TR is the total amount of transfer.19
Table 21 compares social welfare under different tax reforms, now with additional administrative costs. The optimal tax progressivity with administrative costs is the same as that without additional administrative costs, but the optimal capital tax rate is lower without such costs. Raising tax progressivity τ from 0.14 to 0.24 and the capital tax rate τk from 0.24 to 0.34 generates the largest social welfare. (The optimal tax without administrative costs is τ=0.24, τk=0.39.) Welfare gains are as much as 0.60% of permanent consumption, which is 205 thousand in 2010 wons.
There is widespread concern about possible capital outflows when moving to high capital tax and progressive income tax schedule. To address this, we consider tax reforms in an open economy version by fixing the interest rate at the current steady state 6%. Under perfect capital mobility, the difference between household savings (domestic capital) and aggregate capital implied by the fixed interest rate reflects capital outflows (or inflows). We assume that government consumption is a fixed share of (before-tax) aggregate household incomes.20 We also assume that only domestic household incomes are subject to the capital tax. Table 22 reports welfare gains under various tax reforms. The optimal tax reform is virtually the same as that in benchmark economies—increasing tax progressivity (τ) to 0.24 and capital tax rates (τk) to 0.39.
Notes: All numbers are % change (consumption equivalent) from the current steady state.
However, there is a significant capital outflow when the economy moves to high capital tax and more progressive income tax schedule. Table 23 reports the ratio of domestic capital under the new steady state to domestic capital under the current steady state. With optimal tax reform, domestic capital decreases to almost half (47%) of its current level.
We develop a quantitative general equilibrium model and calibrate it to match the salient features of the Korean economy. With this model, we look for the combination of progressivity in the tax function and the capital income tax rate that maximizes utilitarian social welfare. According to our model, a more progressive income tax schedule increases the average welfare of the society. The marginal income tax rates in the 9th decile should increase from the current 22% to 31%. Also, the optimal capital tax rate (39%) is 15 percentage point higher than the current one. Under optimal tax reform, the average household gains welfare by as much as 0.86% of steady-state consumption, which is approximately 300 thousand won per year in 2010 values. The majority (64%) of households are better off, mostly those with low assets and low productivity. More specifically, households in the 1st consumption decile gain welfare by as much as 3.4% of consumption (709 thousand won per year). But, households in the 9th decile lose welfare by as much as 3.4% of consumption (1,656 thousand won per year).
Despite the potential welfare gain from more progressive and high capital income taxes, we would like to note that our results should be interpreted with caution because our benchmark model does not take into account possible capital outflows or the increased administrative costs associated with high income taxes. An open-economy version of our model does indicate that there will be a significant capital flight from a high capital income tax. Sizable administrative costs would also undermine the potential welfare gains from high taxes.
As described in the data section, the tax system in Korea consists of ten national and eleven local taxes. Out of those taxes, three taxes (income tax, corporation tax and value-added tax) account for most tax revenues. In this section, we will describe the detailed tax rates of the three main taxes and social security contributions.
Income Tax: A person, either a resident or a non-resident, is liable to income tax on items of income-derived sources. “Under global taxation, real estate rental income, business income, earned income, and miscellaneous income attributed to a resident are aggregated and taxed progressively. Interest and dividends are subject to tax withholdings” (MOSF 2012, p. 3). Table 24 reports the marginal income tax rates across income brackets. The tax rates on individual income range from 6 percent to 38 percent. When the local income tax is included, the income tax rate ranges from 6.6 percent to 41.8 percent.
Wages and salary incomes are included in taxable income after deductions as specified in Table 25 below. Residents with global income are entitled to annually deduct an amount equivalent to 1.5 million won multiplied by the number of persons in the taxpayer’s family (MOSF 2012). The vulnerable (such as the old and the disabled) and households with many dependent children are eligible for additional deductions.
Corporation Tax: A domestic company is liable to tax on its worldwide income, and a foreign company is liable to tax on its Korean-source income (MOSF 2012). According to the National Tax Service, the marginal tax rates are as below: 10% (11% including the local corporation tax) when the tax base is the same as or less than 200 million won, 20% (22% including the local corporation tax) between 200 million won and 20 billion won, and 22% (24.2% including the local corporation tax) over 20 billion won.
Value-Added Tax: A person who engages in the supply of goods and services and a person who imports goods and services are liable to value-added tax (MOSF 2012). The rate of value-added tax is 10% of added value (National Tax Service 2015).
Social Security: In Korea all citizens must subscribe four compulsory insurance plans: National Pension, National Health Insurance, Employment Insurance, and Workers Compensation Insurance. Contributions to the National Pension are 9% of the wages of workers (employer 4.5%, employee 4.5%) or the income of the self-employed (National Pension Service, 2015). For National Health Insurance, wage workers pays 6.07 % of their wages (employer 3.035%, employee 3.035%) as a contribution, and they also pay additional 6.55% of health insurance contributions for Long-term Care Insurance (National Health Insurance Service, 2015). The contributions of the self-employed are determined by income, wealth and economic status. For Employment Insurance, employees pay 0.65% of their wages and employers pay 2.85% of an employee’s wage. Contributions for Workers Compensation Insurance vary across industries.
The distribution of households, μ(a, x), is time-invariant in the steady state, as are factor prices. We modify the algorithm suggested by José-Víctor Ríos-Rull (1999) in finding a time-invariant distribution μ. Computing the steady-state equilibrium amounts to finding the value functions, the associated decision rules, and the time-invariant measure of households. We search for (i) the discount factor β that clears the capital market at the given annual rate of return of 6%; (ii) the disutility parameter B to match the average hours worked, 0.398; and (iii) the average levels of taxation λ to match net income tax rates, 3.75%. The details are as follows:
1) Choose the grid points for asset holdings ( a ) and idiosyncratic productivity ( x ). The number of grids is denoted by Na, and Nx, respectively. We use Na = 326, Nx = 31. The asset holding at is in the range of [0, 50]. The grid points of assets are not equally spaced. We
assign more points on the lower asset range to better approximate the savings decisions
of households near the borrowing constraint. For idiosyncratic productivity, we construct
a grid vector of length Nx whose elements, lnxj’s, are equally spaced on the interval 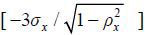 . Then, we approximate the transition matrix of idiosyncratic productivity using Tauchen’s (1986) algorithm.
. Then, we approximate the transition matrix of idiosyncratic productivity using Tauchen’s (1986) algorithm.
2) Pick initial values of β, B, and λ. Given β, B, ρx, σx, and λ, we solve the individual value functions V at each grid point of individual states. In this step, we also obtain the optimal decision rules for asset holdings a'(ai,xj) and labor supply h(ai,xj). This step involves the following procedure:
(a) Initialize value functions V0(ai,xj) for all j = 1, 2, ···, Nx , and j = 1, 2, ···, Nx.
(b) Update value functions by evaluating the discretized versions:
where πx(xj' | xj) is the transition probabilities of x , which is approximated using Tauchen’s algorithm.
(c) If V1 and V0 are close enough for all grid points, then we have found the value functions. Otherwise, set V0 =V1 , and go back to step 2(b).
3) Using a'(ai,xj), πx(xj' | xj) obtained from step 3, we obtain the time-invariant measures μ*(ai,xj) as follows
(a) Initialize the measure μ0(ai,xj).
(b) Update the measure by evaluating the discretized version of a law of motion:
(c) If μ1 and μ0 are close enough in all grid points, then we have found the time-invariant measure. Otherwise, replace μ0 with μ1 and go back to step 3(b).
4) We calculate the real interest rate, individual hours worked, net income tax rate, and other aggregate variables of interest using μ* and decision rules. If the calculated real interest rate, average hours worked, and net income tax rates are close to the assumed ones, we have found the steady state. Otherwise, we choose a new β, B, λ, and go back to step 2.
Individual utilities include those in the transition periods from the initial to the new steady state. We compute the value functions and decision rules backwards and the measure of households forward. Computing the transition equilibrium amounts to finding the value functions, the associated decision rules, and the measure of households in each period. The details are as follows:
1) Compute the initial steady state under the current tax rate. Use the algorithm for the steady-state equilibrium.
2) Choose new tax parameters (progressivity τ, capital tax rate τk) and compute all transition paths as follows
(a) Compute the final steady state under new tax parameters. Use the algorithm for the steady-state equilibrium. However, the discount factor β and disutility parameter B are fixed, and we find the real interest rate where the calculated real interest rate is close to the assumed one. The average level of taxation λ is chosen so that calculated total tax revenues are close to the sum of total transfers and government consumption.
(b) Assume that the transition is completed after T − 1 periods and the economy is in the initial steady state at time 1 and in the final steady state at T . Choose T big enough so that the transition path is unaltered by increasing T .
(c) Guess the capital per effective labor 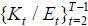 and compute the associated
and compute the associated 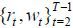 .
.
(d) Guess the path of average level of taxation, 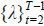 . Note that the average levels of taxation are all different in each period, since
decision rules and measures are different. From backwards, compute the value functions
and policy functions for all transition periods by using VT(●) from the final steady state. Using the initial steady-state distribution μ1 and the decision rules, find measures of all periods
. Note that the average levels of taxation are all different in each period, since
decision rules and measures are different. From backwards, compute the value functions
and policy functions for all transition periods by using VT(●) from the final steady state. Using the initial steady-state distribution μ1 and the decision rules, find measures of all periods 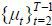 .
.
(e) Based on the decision rules and measures, compute the aggregate variables, tax revenues, transfers and government consumption. If total tax revenues are close to the sum of total transfers and government consumption, we obtain the average level of taxation. Otherwise, choose a new path of the average level of taxation and go back to 2(d).
(f) Compute the paths of aggregated capital and effective labor and compare them with
the assumed paths. If they are close enough in each period, we find the transition
paths. Otherwise, update 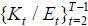 and go back to 2(c).
and go back to 2(c).
3. Choose tax parameters that yield the highest social welfare. This is the optimal tax rate under the utilitarian criteria.
We would like to thank Jiseob Kim, Jay Hong, Chul-In Lee, and Hongchong Cho for the helpful comments on earlier drafts. This work was supported by a grant from the National Research Foundation of Korea funded by the Korean Government (NRF-2014-S1A3A2044238).
Social security contributions including pension and health insurance are proportional to household income.
In many studies on income inequality, household incomes are often adjusted by household size. For example, both the OECD and Statistics Korea use the square root of the household size as an equivalence measure.
Disposable income is defined as market income ( yi ) minus taxes and contributions plus public trans fer income.
The Statistics Agency of Korea announces equivalized market and disposable incomes for the average of each quintile, and at each decile point from the 1st to the 9th.
6 According to the Bank of Korea, average yields of Treasury bonds (3-year), corporate bonds (3-year, AA-), and corporate bonds (3-year, BBB-) between 2000 and 2010 are 5.07%, 6.01%, and 9.93%, respectively. The average inflation rate between 2000 and 2010 is 3.12% (BOK).
Average annual working hours, 2187, from the OECD (2010) are divided by 5,500 hours, which is assumed to be the total amount of discretionary time.
This utilitarian social welfare function has been commonly used in the literature, for example, Aiyagari and McGrattan (1998).
Since we assume consumption tax rate is constant in our model, social welfare is a function of tax progressivity τ and the capital tax rate τk.
We include the welfare of households during the transition from the current steady
state to a new steady state. When a new tax rate is in place in the current steady
state, households start re-optimizing their consumption and hours worked. As a result,
the corresponding paths of the value functions, 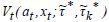 , and the distribution.
, and the distribution. 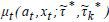 , will be different from those in the old steady state. Hence, the computation of
the optimal tax needs to take into account changes in value functions and distributions
during transition periods until the economy reaches a new steady state.
, will be different from those in the old steady state. Hence, the computation of
the optimal tax needs to take into account changes in value functions and distributions
during transition periods until the economy reaches a new steady state.
Since the average level of taxation, λ, is changing in transitions, marginal and net tax rates in transitions are different from those in the new steady state
We fix the gross tax rates of households at the 2nd decile point instead of at the 1st decile point because the approximation of the HSV function is known to be poor at the very low-income level.
The standard deviations of individual productivity are not symmetric, because the wage process is log normal.
. (1994). Uninsured Idiosyncratic Risk and Aggregate Savings. Quarterly Journal of Economics, 109(3), 659-684, https://doi.org/10.2307/2118417.
, & (1998). The Optimum Quantity of Debt. Journalof Monetary Economics, 42(3), 447-469, https://doi.org/10.1016/S0304-3932(98)00031-2.
, & . (2007). Heterogeneity and Aggregation: Implications for Labor-Market Fluctuations. American Economic Review, 97(5), 1939-1956, https://doi.org/10.1257/aer.97.5.1939.
. (2006). Precautionary Savings or Working Longer Hours. Review of Economic Dynamics, 9(2), 326-352, https://doi.org/10.1016/j.red.2005.11.002.
. (1986). Finite State Markov-Chain Approximations to Univariate and Vector Autoregressions. Economics Letters, 20, 177-181, https://doi.org/10.1016/0165-1765(86)90168-0.