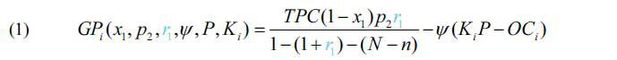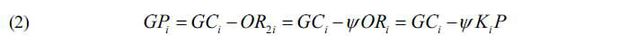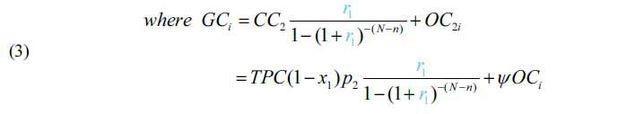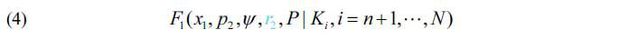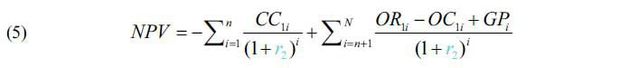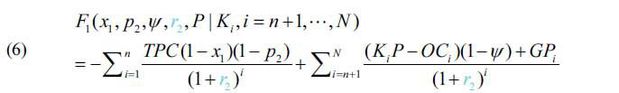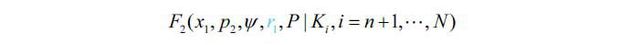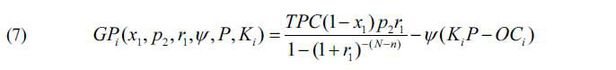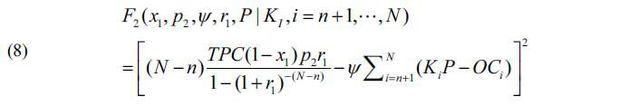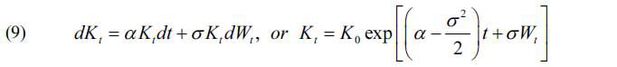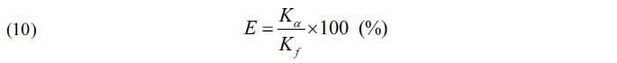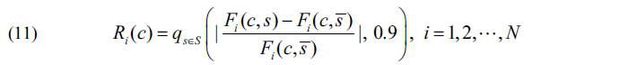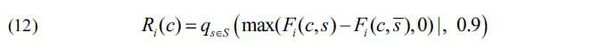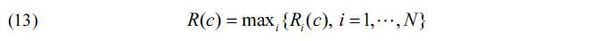Robust Contract Conditions Under the Newly Introduced BTO-rs Scheme: Application to an Urban Railway Project†
Abstract
Few studies have specifically focused on the uncertainty of demand forecasting despite the fact that uncertainty is the one of greatest risks for governments and private partners in PPP projects. This study presents a methodology for finding robust contract conditions considering uncertainty in travel demand forecasting in a PPP project. Through a case study of an urban railway PPP project in Korea, this study uncovered the risk of excessive government payments to private partners due to the uncertainty in contracted forecast ridership levels. The results allow the suggestion that robust contract conditions could reduce the expected total level of government payments and lower user fees while maintaining profitability of the project. This study offers a framework that assists contract negotiators and gives them more information regarding financial risks and vulnerabilities and helps them to quantify the likelihood of these vulnerabilities coming into play during PPP projects.
Keywords
PPP, BTO-rs, Contract Conditions, Robustness, Uncertainty, Forecast, Ridership
JEL Code
R42, R40
I. Introduction
The Korean government started in 1994 to push Public Private Partnership (PPP) projects to encourage private participation in infrastructure investments. By providing various forms of government support, and the PPP model has emerged as a well-established procurement method for many types of infrastructure and public facilities.
Despite such positive aspects, however, PPP projects in Korea face criticism due to unexpected hikes in the government’s payments to private partners through the minimum revenue guarantee (MRG) scheme1 as well as high user fees. Numerous projects, including the Incheon International Airport Expressway and the Nonsan–Cheonan Expressway, have shown that actual out-turn traffic volumes were far below than the contracted traffic agreed-on levels in concession agreements, resulting in higher government payments. In addition, road PPP projects such as the Seoul Ring Expressway are meeting resistance from users due to fees higher than those of publicly financed projects.
Accordingly, the Korean government had made strong efforts to reduce its financial burden and lower user fees by extending concession periods, sharing refinancing gains, and changing the contract conditions through renegotiations with private investors. In particular, the Korean government introduced a risk-sharing scheme for built-transfer-operation (BTO)2 projects in 2015 to low high user fees by reducing private partners’ project risk and to reinvigorate the modality, i.e., the BTO risk-sharing project scheme (BTO-rs).
Even with the BTO-rs scheme, contracted forecasting demand levels for facilities also become one of the most important contract conditions between the government and private partners because unexpected hikes in government payments and user fees are closely linked to the inadequacy in dealing with uncertainty in contracted forecasting demand levels. As the level of contracted demand for a facility increases, the operating income also increases, and this can lower the construction cost subsidy, the level of investment cost sharing by government, and the user fees related to the project. In addition, the lower the contracted demand for the facility is, the higher the government’s construction cost subsidy and investment cost sharing levels become, with a higher level of user fees also arising. Therefore, contracted forecasting demand is the one of most salient risks for the government and private partners when implementing a PPP project. Despite this concern, simple average and aggregated point demand forecasts that ignored the potential for unexpected fluctuations have been used.
The uncertainty in travel demand forecasting is caused by factors such as uncertain input data, limitations of the predictive models used, and the characteristics of the project under analysis. There are compelling reasons for undertaking travel demand forecasting even with deep uncertainty. Travel demand forecasting is conducted through the traditional four-step model where numerous input variables, such as the population and employment rate, are predicted and where it is assumed that the predictions are correct. However, a more suitable expression would be ‘properly estimated’ rather than ‘accurate’. Thus, as the steps progress, due to ‘properly estimated’ data entailing inevitable errors mitigated by inappropriate (or non-realistic) model specifications for each step, the level of uncertainty expands. Biased decisions by analysts also add uncertainty to travel demand forecasting.
To consider the uncertainty in travel demand forecasting, existing approaches assume that the distribution of traffic demand forecasting is known or the uncertainty is calculable. Accordingly, demand forecasting in PPP projects is inadequate when dealing with the uncertainty. Simple average and aggregate point demand forecasts are applied, and negotiations do not take into account unexpected increases in government payments or bankruptcies of projects stemming from the uncertainty in the contracted forecasting demand.
The explanatory approach known as robust decision making (RDM) is a promising tool for dealing with uncertainty in travel demand forecasting. RDM, exploring acceptable policies under deep uncertainty is mainly applied to topics such as water resource management, disaster prevention, and climate change, all of which entail relatively large events with extended analysis periods. However, recently, the scope of these subjects is being expanded, with RDM now applied to various disciplines. Using RDM, it is possible to approach the travel demand forecast problem more reasonably. The RDM approach tests possible future states specified by a wide range of decision spaces, with these utilized for characterizing areas of vulnerability (Marchau et al., 2019). As such, the method is readily applicable to travel demand forecasting, as unpredictability is part of the method. The framework of the RDM approach, termed the inversed ‘predict-then-act’ framework, easily finds factors that could not be identified by the existing ‘predict-then-act’ scheme. Thus, it enables more explanatory, rational and adaptive policy establishment outcomes for the future.
The purpose of this study is to apply the RDM approach to present a methodology for finding robust contract conditions3 which minimize negative effects on governments and private partners considering the uncertainty in travel demand forecasting in PPP projects. In other words, this study suggests acceptable and robust BTO-rs contract conditions to ensure the best performance of a PPP project. Because this unlike forecast-then-contract approaches, this study suggests bottom-up decision making regarding the contract condition for dealing with vulnerability properly and minimizing any negative effects caused by uncertainty in demand forecasting.
The remainder of the study proceeds as follows. Chapter I presents the study’s purpose and background and Chapter II introduces the concept of uncertainty in demand forecasting and existing methods that attempt to consider uncertainty. This chapter also presents a literature review of PPP contracts assuming that the uncertainty in demand forecasting is controllable or the result of demand forecasting is accurate. Chapter III introduces the concept of the BTO-rs scheme with a schematic representation of typical cash flows. This study also involves a case study of an urban railway PPP project. Chapter IV presents the case study, currently ongoing in the Seoul Metropolitan Area (SMA) in Korea, to derive the acceptable range of BTO-rs contract conditions given uncertainty in ridership forecasting. Chapter V specifies the decision variables, objective functions and an uncertainty variable with which to conduct the RDM approach. A multi-objective function is developed to establish the interest of the government and private partner with a focus on minimizing of government’s payments (GP) and maximizing the project’s NPV, and the objective functions are optimized to derive the plausible range of contract conditions under the BTO-rs scheme.
Chapter VI presents a regret-based robustness evaluation criterion, through which various feasible contract conditions are evaluated and a vulnerability analysis is conducted to find robust contract conditions. Based on the analysis, Chapter VII summarizes the results of this study, presents the conclusion, and discusses limitations.
II. Related Literature
There have been several studies of the conditions of contracts related to demand forecasting in PPP projects. However, all of them assumed that the uncertainty in demand forecasting is controllable and all were based on the ‘predict-then-act’ concept, the opposite of the 'bottom-up' concept, which is the basic analysis framework of RDM. These approaches start with the assumption that uncertainty is predictable and that the error specification is wide enough to represent the future. However, a fundamental problem is that if the prediction is not correct, subsequent decisions are subject to higher rates of incorrectness.
Yang and Meng (2000) analyzed optimal capacity and toll levels for PPP road projects with an ‘assumed’ accurate point estimate for future traffic volumes. Chen et al. (2003) developed a multi-objective programming model to maximize private investors’ expected profits and minimize the risk of projects. They simultaneously obtained the optimal toll and capacity for a BOT-road project using a multi-objective genetic algorithm with the assumption of the traffic volume as a random variable. Tan and Yang (2012) analyzed tolls, concession periods, and government subsidies according to the degree of flexibility in a PPP project contract. They considered the uncertainty in traffic demand forecasting using observed traffic volumes but failed to reflect the future growth and volatility of the traffic volume. Feng et al. (2016) designed a negotiation process in a PPP project as a two-stage optimization problem and computed a government payment schedule according to toll scenarios. They showed that renegotiations occur in a BOT road contract when the investor’s behavior due to loss aversion is at a sufficiently low level. However, this approach lacks consideration of the uncertainty in traffic demand forecasting. Zhang et al. (2018) also compared socially optimal prices of tolls, road capacities, and concession periods under a single period concession structure and a two-period concession structure of BOT PPP contracts without reflecting the uncertainty of traffic demand forecasts.
In addition, PPP contract specification problems have been studied with a rather narrow vision toward future states, as contract specifications are countable. Accordingly, the problem is often framed within a limited number of scenarios. In such studies, a binomial lattice is a preferred modeling scheme for dealing with contract specifications, as it branches all possible scenarios related to future changes with a tree structure. Similar to the binomial lattice, Bowe and Lee (2004) utilized the log-transformed binomial valuation model developed by Trigeorgis (1996) for valuing several compound options associated with a high-speed rail project in Taiwan. This binomial valuation method was further developed (Ho and Liao, 2011) by integrating fuzzy theory in order to reflect forms of flexibility in investment decisions, such as expansions, extensions, or even the abandonment of an underlying project.
As such, previous studies researched PPP contract conditions such as toll levels, road capacities and concession periods based on the simple assumption that the uncertainty of demand forecasting is calculable and the results of demand forecasts are accurate. However, this paper considers the uncertainty of demand forecasting as incalculable.
Due to the limitations of existing studies, the PPP contract conditions associated with travel demand forecasting must be approached with RDM, which examines the existence of deep uncertainty. RDM (Lempert and Collins, 2007) identifies potential strategies, evaluates trade-offs by calculating the vulnerabilities of such strategies, and conducts adaptive decision making. Recently, Kasprzyk et al. (2013) proposed the method of multi-objective robust decision making (MORDM), which expands RDM to a decision-making issue featuring the functions of multiple objectives. Adopting this multi-objective function helps stakeholders navigate the space of feasible strategies and discover alternatives using optimal trade-offs. That is, unlike the ‘predict-then-act’ or ‘top-down’ approaches to policy that assume an accurate forecast, RDM is a bottom-up approach and develops contract conditions which deal with vulnerability while also minimizing any negative effects due to deep uncertainty. RDM, which tests a significant number of cases and seeks to construct scenarios using the identified vulnerabilities caused by deep uncertainties, is suitable for dealing with uncertainty in travel demand forecasting, which shows a wide range of change, even from day to day.
III. Built-Transfer-Operation (BTO)-rs scheme
The Korean government had been striving to reduce its financial burden and lower user fees, and it introduced a risk-sharing scheme for built-transfer-operation (BTO) projects in 2015. In the BTO scheme, investment and operating risks belong to the private partner; however, the investment and operating risks are shared by the government and the private partner at a certain ratio, and both share excess profits or losses under the BTO risk-sharing (BTO-rs) scheme.
If the share of the investment costs between the government and the private partner is evenly split, the private partner can receive a certain portion of the operating costs from the government when demand for the infrastructure facility or service is not sufficient. However, when demand exceeds the contracted forecast, the government receives a partial return of the private partner’s profits. Because the government shares a portion of the private sector’s investment risk, the rate of return of the private partner’s investment is reduced, ultimately lowering user fees associated with the project as well.
Figure 1 presents a schematic explanation of the cash flow under the BTO-rs scheme. As shown in the figure, important contract conditions in the BTO-rs scheme are the ratio of investment cost sharing by the government to the total private investment (p2), the ratio of excess profits or losses shared by the government to the operational profits or losses (Ψ), the ratio of the construction subsidy toward the total project cost (x1), the level of user fees (P), and ridership for operational year i(Ki). When p2 and Ψ are both zero, there is no government risk sharing for private investment, meaning that this situation is identical to the BTO scheme, where only a construction subsidy exists.
There is a construction subsidy for cash-in during the construction period (from 1 through n), and the construction subsidy by the government can be expressed as the total project cost (TPC) of the project multiplied by the ratio of the construction subsidy (x1). Additionally, there are two items for cash outflows during the construction period in the BTO-rs scheme; these are related to the private partner’s investment cost. The first is the private partner’s investment cost excluding the shared investment cost by the government (CC1), and the second is the shared investment cost by the government as part of the private partner’s investment cost (CC2). Here, the CC1 can be converted as CC1=TPC(1-x1)(1-p2) and CC2 can be determined from the total project cost (TPC) excluding the government’s construction subsidy multiplied by the ratio of investment cost sharing by the government to the total private investment cost (p2), CC2=TPC(1-x1)p2.
During the operational period (from n+1 through N), he cash inflow contains two items: the government’s payment (GP) for the shared cost by the government among the private partner’s investment (CC2)4 and the operating revenue attributable to the private partner (OR1). Here, the government’s payment (GP) can be calculated by GP=CC2×(1+r1), where r1 denotes the private partner’s expected rate of return for the CC2. In addition, OR1 can be expressed as OR1=OR(1-Ψ)=K×P×(1-Ψ), where OR indicates the operating revenue. The cash outflow during the operational period (N-n) is the operating cost borne by the private partner (OC1). OC1 can be expressed as the operating cost of the project (OC) multiplied by one minus the ratio of excess losses shared by the government to the operational losses (Ψ), OC1=OC(1-Ψ).
Therefore, the government’s payment during operational year i, GPi, can be expressed through the following function and is paid annually to private investors.
Here, Ki is the contracted ridership forecast and OCi is the operating cost for operational year i.
Under the BTO-rs scheme, the government’s payment during operational year i(GPi) occurs when the risk sharing base amount (GCi) for year i exceeds the attributable operating revenue to the government (OR2i) for year i. However, when OR2i exceeds GCi, there will be a reimbursement to the government corresponding to the difference for operational year i. Therefore, GCi is the base amount that determines whether the government pays or is reimbursed during year i.
GPi and GCi can be specified as follows:
IV. Case Study: Urban Railway PPP Project
This paper conducts a case study of an urban railway PPP project, referred to as the A-Line project, currently ongoing in the Seoul Metropolitan Area (SMA) in Korea, to derive the acceptable range of the contract conditions under the uncertainty of ridership forecasting.
The Ministry of Land and Transport (MOLT) put out a request for proposals (RFP) for the A-Line as a BTO-rs scheme in December of 2017 after assessing the project’s profitability, benefit to the public, user affordability, and efficiency gains. Two bidders forming a consortium of builders, maintenance operators, and financial institutions submitted project proposals to the MOLT, and the MOLT started negotiations with the preferred bidder from May of 2018. However, the MOLT and a private concessionaire concluded an agreement that the project would proceed in October of 2018 as a standard BTO project due to the possible negative effects of BTO-rs contract conditions.
The A-Line’s length is 43.6km, and it is designed to pass through five stations. The total project cost was KRW 2,901.7 billion, of which KRW 1,373.7 billion was subsidized by the government and KRW 1,702.1 billion came from an investment by a private partner. The private concessionaire has the right to operate the A-Line for 30 years (See Table 1 for more details), with this contract expiring in 2054.
Table 1 presents the concessionaire’s proposal for the BTO-rs scheme and the contracted conditions under the BTO scheme. Under the BTO-rs scheme, the concessionaire had requested 21.2% of the construction cost as a subsidy from the MOLT, while in the BTO contract, they concluded that 47.3% of the total project cost (TPC) would be paid by the government as a construction subsidy.
TABLE 1
PROPOSAL IN THE BTO-RS AND CONTRACTED CONDITIONS IN BTO
Source: MOLT, “A-Line Concession Agreement,” 2018.
The contracted forecast ridership set by the contract is 73,159,276 passengers in 2024, the first year of service. After the opening year, the contracted forecast ridership (Ki) increases steadily to 89,366,742 passengers in 2026, after which it deceases to 2045. The contracted forecast ridership remains fixed for ten years after 76,163,655 passengers in 2045.
Table 2 and Figure 2 show the contracted forecast ridership based on which the agreement between the concessionaire and the government was made.
TABLE 2
YEARLY CONTRACTED FORECAST RIDERSHIP (Ki)
Source: MOLT, “A-Line Concession Agreement,” 2018.
The initial tariff on the first service date was contracted as the sum of the basic fare and travel distance fare. The basic fare was KRW 2,592 and the travel distance fare was KRW 216 for every 5 km. Subsequent fare adjustments are applied based on the cumulative monthly changes in the consumer price index (CPI) once a year, and the concessionaire reports this figure to MOLT after the fare change. Meanwhile, the basic fare was proposed as KRW 2,419 and the travel distance fare was KRW 216 for every 5 km under the BTO-rs scheme.
V. Optimal Contract Conditions under the BTO-rs scheme
A. Objective Function
A multi-objective function is developed to establish the interest of the government and the private partner, i.e., to minimize the total government’s payments (GP) for the entire operational period while maximizing the project’s NPV. The objective functions are optimized to derive the acceptable range of contract conditions under the BTO-rs scheme.
1. Objective Function for the Private Partner: F1
The first objective function is to maximize the NPV of the project and to search for optimal contract conditions, such as (x1, p2, Ψ, r2, P) given the ridership for operational year i.
Here, r2 is the expected rate of return for the government’s shared cost of the private investment.
The private partner seeks to maximize the NPV of the project. The NPV function under the BTO-rs scheme is formulated as follows:
Using equation (5), the first objective function under the BTO-rs scheme can be expressed as shown below. The NPV increases as P, x1, and p2 increase. However, the NPV decreases as Ψ increases.
2. Objective Function for the Government: F2
The second objective function is to minimize total government’s payments (GP) for entire operational period. The objective of the government can be expressed in the form of various interests, such as maximization of social welfare or benefits and the provision of the service in time at a reasonable user fee level given applicable budget constraints. However, minimizing GP is set as an objective of the government, as the other interests are already considered or resolved during the project appraisal process.
Under the BTO-rs scheme, GPi occurs when GCi exceeds OR2i. GPi can be expressed by the following function, which includes the variable, p2, the corresponding rate of return of the private partner’s investment (r2), Ψ, x1, P and Ki.
Accordingly, the government’s payments (GP) for the entire operational period can be established using the following equation:
The government’s payment is squared because it is assumed that the government minimizes unexpected increases in government payments to private investors arising from the BTO-rs scheme and does not seek to maximize financial revenue.
B. Narrowing Down to Plausible Contract Conditions
The contract conditions as decision variables for optimizing the objective functions in this paper are p2, Ψ, and x1, given the contracted forecast ridership figure for operational year i(Ki). We exclude other contract conditions P, r1 and r2 for simplicity and for the convenience of the calculation. The value of r1, indicating the expected rate of return for private investment, is set to 5.2%, which is the contracted IRR of the A-Line project. Additionally, r2 is set to 1.02% and is the level of the interest rate on Korea’s government bonds. This implies an expected rate of return for the government’s shared cost in the private investment. Regarding the range of P, it was increased from KRW 2,000 in KRW 100 intervals to a maximum of KRW 3,000, and sets of contract conditions (p2, Ψ, x1) are identified by optimizing the objective functions.
Before the robustness tests of the contract conditions are carried out, it is desirable to reduce the contract conditions to an ensemble of plausible futures. The study resolves this issue by restricting the range of the contract conditions and further by removing infeasible contract conditions. In particular, the set of feasible contract conditions is identified through a multi-objective optimization process using a genetic algorithm.
The initial values for p2, Ψ and x1 are obtained from the proposed BTO-rs contract conditions for the A-Line project (x1=16% , p2=40% , Ψ=1%). In addition, the upper limit of x1 is set to 50%, which is the largest construction subsidy ratio for a railway PPP project in Korea.
Table 3 shows the initial value and lower- and upper-limit values for the determined contract condition variables (x1, p2, Ψ).
The NSGA-II algorithm (Hadka et al., 2015) is used to identify feasible sets of contract condition variables that optimize the two objective functions. In the NSGA-II algorithm, if the initial solutions are given in the search space of the decision variables, a new set of candidate solutions is created through genetic modification (crossover and mutation), and individual candidate solutions are repeatedly evaluated during the search for optimal solutions. This paper generated 400 initial contract conditions (x1, p2, Ψ) given the levels of P, r1 and r2 contracted the forecast Ki, and created offspring through crossover and mutation. The evolution process is repeatedly applied to a set of offspring more than 100 times.
The set of (x1, p2, Ψ) that optimizes the objective functions is an approximate solution for the frontier that considers the offsetting effects of government payments and the project’s NPV while being simultaneously deemed a set of selectable contract conditions.
C. Feasible Contract Conditions
The fare (P) is increased from KRW 2,000 in increments of KRW 100 to a maximum of KRW 3,000 and the sets of contract conditions (x1, p2, Ψ) are investigated under the given levels of P, r1 and r2 and the contracted forecast Ki.
Of the optimal set of (x1, p2, Ψ), sets of contract conditions that are deemed infeasible for both private investors and the government are excluded owing to the project’s negative NPV, rendering the project itself unsustainable, and when the government’s payment is very high. In particular, we exclude the set of contract conditions for which government payments exceeded KRW 30 million during the operational period and produced a negative NPV outcome.
Table 4 shows the 18 optimal sets of contract conditions (x1, p2, Ψ), the corresponding government payments, and the project’s NPV under the given P after excluding infeasible contract conditions. The ratio of the construction subsidy to the total project cost (x1) is found to be close to the maximum value of 50%, and the ratio of excess profits or losses shared by the government to the operational profits or losses (Ψ) shows a rate of less than 20%.
TABLE 4
OPTIMAL CONTRACT CONDITIONS (x1, p2, Ψ), GP, AND NPV
Note: The table presents only contract conditions that are feasible for both private investors and the government.
Under the [No. 1] contract condition, x1 is 48.25%, close to the maximum of 50%, while p2 and Ψ are insignificant at 1.44% and 0.51%, respectively. It was also found that the NPV is approximately 458.9 billion won and that no additional government payment had arisen. In particular, the analysis showed that it is possible to conclude a contract at fare 2,000 won, which is much lower than the current BTO project user fee of 2,700 won. Under the [No. 4] contract condition, x1 is calculated at 39.22%, which is far below the 50% maximum. However, p2 and Ψ are also insignificant at 3.67% and 1.40%, respectively. The fare level is 2,100 won, which is lower than 2,700, and the NPV is 411.8 billion won. It was also found that no additional government payments had occurred.
Under the [No. 10] contract condition, where the user fee is 2,500 won, x1 is 3.84% which is lower than any other contract conditions. However, Ψ shows the highest level, at 19.79%. As a result, the NPV is slightly lower at around KRW 717.8 billion. For the [No. 18] contract condition, where the NPV is largest, x1 and p2 are found to be highest.
VI. Robust Optimal Contract Conditions
We identified sets of contract conditions that optimize the two objective functions of maximizing the project’s NPV and minimizing the government’s payments (GP). In the analysis thus far, however, the contracted forecast ridership for operational year i(Ki) is used, consisting of the simple average and aggregate ridership forecasts and assuming that the ridership forecasts are accurate.
This section considers the uncertainty of ridership forecasts. By assuming that the probability distribution of ridership forecasting is not known and the uncertainty is not calculable or controllable, this paper suggests robust contract conditions that minimize the government payment and maximize the project’s NPV, while also limiting the ranges of the variances in the government payment and the NPV in most situations.
A. Uncertainty in Forecasted Ridership
To characterize uncertainty in ridership forecasts for the 30-year operation period, this paper assumes that the ridership forecast follows geometric Brownian motion (GBM) (see Kim et al., 2012 and Kim, 2017), with GBM including all possible effects of the ridership forecasts caused by the uncertain variables. GBM, a model widely used in financial engineering, is used to predict the movements of variables with deep uncertainty (see Martin and Rennie, 1996). In the GBM model, once variables move in one direction, the probability of moving in the same direction increases. This phenomenon is observed in actual travel demand. It should be noted that any specification method such as random sampling or bootstrapping can be applied for uncertainty specification of the ridership forecast. According to GBM, the forecasted ridership of the A-Line during year t is dependent on the increasing rate (α) and corresponding volatility (σ) (Eq. [9])
Here, Kt is the ridership of the A-Line in year t and K0 is the ridership in the first year of service. Wt is the standard Wiener process that follows a normal distribution, where the average is 0 and the standard deviation is 1. α is the increasing rate of ridership and σ is the corresponding volatility.
The ridership for the opening year (K0) in equation (9) is generated based on the probability distribution of the ridership forecasting error (E) in currently operating Korean PPP projects. After defining the ridership forecasting error (E) as the forecasted ridership (Kf) relative to the actual out-turn ridership (Kα), K0 is then generated using a random number (e) of the probability distribution of E and Kf.
Note that Kf is the contracted forecast ridership for the commercial operational year of the A-Line, which in this case is 3,159,276 passengers.
The parameters of the probability distribution of the ridership forecasting error
(E) are estimated using the actual out-turn ridership in the currently operating PPP
projects, i.e., the Incheon Airport Railroad, New Bundang Line, SMA Line 9, Busan-Gimhae
Light Railway and the Uijeongbu Light Railway. Meanwhile, to generate Kt, the increasing rate of ridership (α) and its volatility (σ) are applied from the actual observations of the above PPP projects. They are currently
running throughout the Seoul Metropolitan Area, where the A-Line is located. In particular,
the study considers the ramp-up effect of ridership during the operation year by applying
different increasing rates of α and σ. Ramp-up refers to the phenomenon of the actual ridership changing. The ridership
fluctuates during the early service period, but it is expected to stabilize over time.
This study found that the number of passengers was highly volatile during the first
six years after the opening of the service, after which it stabilized (SMRTC, 2008).
Accordingly, this paper sets α1 and σ1 to 0.147 and 0.097, respectively, from the opening year to the sixth year of the
service, and sets α2 and σ2 from the seventh year to the thirtieth year of service to 0.0147 and 0.0097, respectively,
values which are assumed, correspondingly, to be 10% of α1 and σ1. Meanwhile, to consider the wide range of possible values of Kt, a combination of α and σ is used. The minimum and maximum values of α and σ are set to 50% and 150% of the reference values in each case, with Kt then generated using a combination of values of α and σ within these limits. Accordingly, from the opening year to the fifth year of service,
we assume that the probability distributions of α1 and σ1 follow uniform distributions with a lower limit of 50% and an upper limit of 150%
around the baseline values 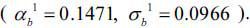 Meanwhile,
Meanwhile, 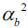 and
and 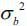 are assumed to be 77% (1/1.3) of
are assumed to be 77% (1/1.3) of 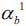 and 71.4% (1/1.4) of
and 71.4% (1/1.4) of 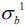 , respectively
, respectively 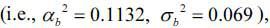 from the sixth year to the thirtieth year of service.
from the sixth year to the thirtieth year of service.
B. Variations in GP and NPV caused by the uncertainty in ridership forecasts
This section identifies the variations of GP and NPV given the 18 sets of contract conditions (P, x1, p2, Ψ) according to the uncertainty of the forecasted ridership. To do this, Kt is generated five hundred times using random numbers of the uniform probability distributions of α and σ and the exponential distribution of the ridership for the opening year (K0).
Table 5 shows the mean and standard deviation of GP and NPV of the project in the 18 sets of contract conditions caused by the uncertainty of ridership forecasts. For instance, in the [No. 1] contract condition, mean and the corresponding standard deviation of GP are 21.12 and 12.04 billion, respectively. The corresponding NPV ’s mean and standard deviation are KRW 661.64 and KRW 1217.00 billion, respectively. Among the 18 sets of optimal contract conditions, the standard deviation of GP is small in the order of [No. 1], KRW 12.04 billion; [No. 4], KRW 34.47 billion; and [No. 2], KRW 64.98. The standard deviation of NPV is small in the order of [No. 3], KRW 802.23 billion; [No. 5], KRW 871.14 billion; and [No. 10], KRW 924.09 billion.
The [No. 10] contract condition shows the highest expected GP, while the highest NPV occurs in the [No. 18] contract conditions. These results show that there is a risk of excessive government payments to the private partner as well as non-profitability of the project due to the uncertainty of ridership forecasting.
C. Robust Contract Conditions under Ridership Forecasting Uncertainty
This section presents robust contract conditions among the 18 sets of contract conditions that minimize any unforeseen increase in government payments and the deterioration of the viability of the project as possibly caused by ridership forecasting uncertainty.
The robustness evaluations of the 18 sets of contract conditions are conducted considering the following regret-based measures presented by Herman et al. (2015). Herman et al. (2015) defined the robustness evaluation indicator Ri, for objective function i as the rate of change of the objective function i relative to the predetermined baseline value of the objective function.
Here, q(•, 0.9) refers to the ninetieth percentile and Fi(c, s) refers to the value of the objective function i consisting c and s. In addition, c refers a set of contract conditions (x1, p2, Ψ) and s is the element of S, which is a set of parameters related to the uncertainty of the ridership forecast, K0, α and σ. Moreover, s represents the baseline values of K0, α and σ, and N refers to the number of objective functions, a value which is two here.
The denominator, which is the value of the objective function Fi(c,s), can be zero in equation (11). Accordingly, this paper adopted the robustness evaluation indicator Ri as the robustness value. It is defined as shown below.
Meanwhile, when the values of the respective objective functions have identical units and are comparable, the upper limit of Ri can be used as the regret-based measure, and the ninetieth percentile of the set of contract conditions is assumed contains robust contract conditions.
Table 6 shows the 18 sets of optimal contract conditions (x1, p2, Ψ) and the corresponding values of R1 and R2. If R1, indicating the robustness measure of F1, is large, it can be said that the NPV of the project fluctuates considerably according to the uncertainty of the ridership forecasts. If R2 is small, it can be said that GP changes only slightly according to the uncertainty of the ridership forecasts, and the contract condition is a robust condition which enables the government to minimize the vulnerability and negative results of GP . Accordingly, R2 shows the largest value in the [No. 10] contract condition, whereas for R1, [No. 18] has the largest value. R2 is small in the order of contract conditions [Nos. 1, 4, 2], where p2 and Ψ are insignificant. This arises because with smaller values of GP, p2 and Ψ, less change occurs in GP. On the other hand, the R1 values are small in the order of the [No. 2], [No. 1], [No. 10] and [No. 4] conditions.
Considering R1 and R2 at the same time, the sets of contract conditions [No. 1], [No. 2] and [No. 4] are suggested to be the most desirable robust contract conditions for the A-Line project, as they minimize unforeseen increases in government payments and the deterioration of the viability of the project possibly caused by uncertainty in the ridership forecasts.
The robust contract conditions suggest x1 as 48.25%, 49.57% and 39.22%, respective to the conditions above. They also correspondingly suggest p2 as 1.44%, 7.79% and 3.67% and Ψ as 0.51%, 2.68% and 1.40% in [No. 1], [No. 2] and [No. 4].
D. Comparison Total Government Payment and User Fee between the BTO-rs and BTO Schemes
MOLT put out a request for proposals (RFP) for the A-Line project as a BTO-rs scheme; however, MOLT and a private concessionaire concluded an agreement that the project will be processed as a standard BTO project due to the possible negative effects caused by the BTO-rs contract conditions. In this section, the total government payment and fare level amounts are compared between the suggested 18 contract conditions and a current BTO contract condition.5 Here, the total government payment is the amount including the construction cost subsidy by the government for the BTO contract and GP as well as the construction subsidy in the case of BTO-rs scheme. In the current BTO contract, 47.3% of the total project cost is paid by the government as a construction subsidy, and the user fee is KRW 2,707.
Note that contract conditions [No. 1], [No. 2] and [No. 4] were robust contract conditions under the BTO-rs scheme. Table 7 shows that the total expected government payments in contract conditions [No. 4] and [No. 10] are smaller than those of the current BTO contract among the 18 contract conditions. The fare levels are also KRW 2,100 and KRW 2,500, respectively, which are lower than the KRW 2,707 of the current BTO contract. However, the [No. 10] contract condition is not robust and is exposed to the risk of incurring additional government payments due to the uncertainty of ridership forecasts. In addition, for the [No. 2] contract condition, suggested as a robust contract condition under the BTO-rs scheme, the total expected government payment for the project is KRW 1,551.76 billion, which exceeds the value of KRW 1,373.7 billion under the current BTO contract. Accordingly, the [No. 4] contract condition is more suitable under the BTO-rs scheme from the perspective of the government and users. The total government payment is estimated to be KRW 1197.95 billion under the [No. 4] contract condition.
VII. Summary and Conclusion
PPP projects in Korea face criticism due to unexpected hikes in the government’s payments to private partners and high user fees. Accordingly, the Korean government has been striving to reduce its financial burden and lower user fees, and it introduced the BTO-rs scheme to lower the high user fees by reducing the project risk borne by private partners.
This paper suggested robust BTO-rs contract conditions that minimize negative effects on governments and private partners considering the uncertainty in ridership forecasts. The sets of contract conditions for which government payments resulted in more than KRW 30 million for the operational period and negative NPV outcomes were excluded, and robust contract conditions that could reduce government payments and user fees while maintaining clear profitability of the project were selected. When we compared the robust contract conditions of the current BTO contract and determined the total expected government payment in the [No. 4] condition, we suggested x1, p2 and Ψ rates of 39.22%, 3.67% and 1.40%, respectively, which were lower than those of the current BTO contract. In addition, the fare level was KRW 2,100, which is lower than the KRW 2,707 of the current BTO contract.
Several areas can be suggested for further study. In this paper, the GBM model is adopted to determine the probability distribution of the forecasted ridership. It should be noted that the generated ridership depends on the probability distribution of the GBM, which could, in turn, can change the robust contract conditions. Further research on the probability distribution of the ridership are needed. Finally, further research is needed with regard to how much weight should be assigned toward each object function to derive more practical and reliable contract conditions.
Notes
This paper is based on Kim, 2019, A Study on the BTO-rs Contract Conditions under the Uncertainty of Operation Revenue, Working Paper 2019-02, KDI (in Korean). I am grateful to Jinho Kim for his outstanding assistance and to two anonymous referees for their valuable comments.
In the MRG scheme, the government guarantees the predetermined contract revenue through government payments when the actual outturn revenue falls below the contract revenue.
In a BTO contract, the private partner builds the infrastructure, transfers ownership to the government and operates for a concession period to recoup its investment. Meanwhile, in a BTL contract, the private partner builds the infrastructure, transfers ownership to the government and recoups its investment through government payments.
Robust contract conditions are defined as those that minimize government payments and maximize the project’s NPV while also limiting the range of variance in the government's payments and NPV levels in most situations.
References
, & (2004). Project evaluation in the presence of multiple embedded real options: evidence from the Taiwan High-Speed Rail Project. Journal of Asian Economics, 15, 71-98, https://doi.org/10.1016/j.asieco.2003.12.001.
, , & (2003). Mean-variance model for the build-operate-transfer scheme under demand uncertainty. Transport Res Rec, 1857(1), 93-101, https://doi.org/10.3141/1857-11.
, , , & (2016). Subsidizing and pricing private toll roads with non-contractible service quality: a relational contract approach. Transport. Res. Part B: Methodological, 91, 466-491, https://doi.org/10.1016/j.trb.2016.04.017.
, , , & (2015). An Open Source Framework for Many-objective Robust Decision Making. Environmental Modelling & Software, 74, 114-129, https://doi.org/10.1016/j.envsoft.2015.07.014.
, & (2011). A fuzzy real option approach for investment project valuation. Expert Systems with Applications, 38(12), 15296-15302, https://doi.org/10.1016/j.eswa.2011.06.010.
, , , & (2013). Many objective robust decision making for complex environmental systems undergoing change. Environ. Modell. Software, 42, 55-71, https://doi.org/10.1016/j.envsoft.2012.12.007.
, & (2007). Managing the Risk of Uncertain Thresholds Responses: Comparison of Robust, Optimum, and Precautionary Approaches. Risk Analysis, 27, 1009-1026, https://doi.org/10.1111/j.1539-6924.2007.00940.x.
, & (2012). Flexible build-operate-transfer contracts for road franchising under demand uncertainty. Transportation Research Part B: Methodological, 46(10), 1419-1439, https://doi.org/10.1016/j.trb.2012.07.001.
, & (2000). Highway pricing and capacity choice in a road network under a build-operate-transfer scheme. Transport. Res. Part A: Pol. Pract., 34(3), 207-222, https://doi.org/10.1016/S0965-8564(99)00001-4.
, , & (2018). The effects of concession period structures on BOT road contracts. Transport. Res. Part A: Pol. Pract., 107, 106-125, https://doi.org/10.1016/j.tra.2017.11.018.