
- P-ISSN 1738-656X


Although the patient’s problem with access to health information has been improved due to rapidly developing information technologies, such as the internet, some patients still do not have enough ability to understand, interpret, and analyze the health information. Given this view on the patient’s asymmetric information problem, if a doctor provides sufficient effort to help patients understand and interpret medical information, the efficiency of patient’s medical care use could be improved.
This paper shows firstly that the patient’s inefficient use of medical care originates from his information problems, such as the misperception of the effectiveness of medical care and secondly suggests that if the doctor makes sufficient effort to correct patient’s information problems, the inefficiency can be ameliorated. This paper also suggests the manipulation of a doctor’s payment method can lead a doctor to provide optimal level of efforts which can in turn lead patients to use the optimal level of medical care. With an optimal level of effort, a doctor can more easily achieve a patient’s compliance with the newly recommended amount of medical care.
Patient’s Asymmetric Information Problem, Efficiency of Patient’s Medical Care Use, Doctor’s Effort, Doctor’s Rate of Supply-side Cost Sharing, 환자의 비대칭적 정보의 문제, 환자의 의료서비스 이용의 효율, 의사의 노력, 의사의 공급 측면의 비용 부담 비율
I10, I11, I18
Nowadays patients have better access to information about their health states and about the effectiveness of new or existing medical treatments, as a result of rapidly developing information technologies. For example, a woman who is pregnant with her first child is likely to need information about the first trimester of her pregnancy: morning sickness, home remedies, and when to call her physician. An email containing such information could show up on her desktop computer just before she gets morning sickness. The email which has this kind of information might allow a woman to have a comfortable experience with pregnancy, as she is less concerned, makes fewer calls to her physician, and knows when she should call her doctor. Therefore the patient’s efficient use of medical care through informed decision-making might have a role in suppressing the rapidly increasing expenditure on health care, and this is a significant role of consumer health information (Brunt, 1998).
However, a patient’s enhanced accessibility to health information mentioned above might make the patient’s decision-making process more complicated, which means a patient still has a problem with efficiently utilizing health information. In other words, what a patient needs for his1 efficient medical care use is not just health information per se, but is the ability to understand, interpret, and analyze the health information or medical knowledge.
We may find that a patient’s asymmetric information problem caused by his inability to understand or interpret health information plays a key role in his decision making process. Whenever an individual feels sick, he has to make a medical decision of whether to consult a doctor, given his own evaluation of his health state, based on his own health information concerning his health problems (Arrow, 1963). Once he visits a doctor, a patient will make a decision whether or not to comply with a doctor’s recommendation for medical treatment, given the medical information provided about this treatment by his doctor.
Furthermore, as Lee (1995) suggests, a patient’s compliance with a doctor’s recommendation for medical treatment might depend on a patient’s expectation of marginal benefit from utilizing medical care, which would be formalized by his own interpretation or understanding of the medical information about the effectiveness of the medical treatment that doctor provides. Even if the medical information from a doctor is based on objective clinical data, the patient must make an effort to understand and interpret that medical information (Lee, 1995). So the difficulty in understanding medical information might result in the patient’s expectation about the marginal benefit of medical treatment being biased from the correct one, and the patient’s inability to understand and interpret medical information could be a factor distorting his efficient medical care use. As a patient is forming his own perception on the effectiveness of medical care, a doctor might affect this process by helping the patient understand and interpret the information relevant to the patient’s health state and the effectiveness of medical treatment, by way of closely communicating with the patient (Deber, 1994).
Therefore, by building up the general equilibrium model, this study tries to show that a patient’s inefficient use of medical care originates from his problem with asymmetric information and that a doctor’s effort in correcting a patient’s information problem could lead a patient to efficiently using medical care. Based on this exploration, this study also shows a doctor’s payment method, specifically a doctor’s rate of supply-side cost sharing, can induce a doctor to sufficiently provide effort.
The organization of this paper is as follows: Section II explores the patient’s decision-making process for deriving the optimal demand for medical care. In Section III we explore the doctor’s decision-making process in deriving the optimal supply of medical care and effort. In Section IV, the equilibrium price and quantity of medical care are derived and its efficiency tested. In Section V, comparative static analyses are performed to show the effect of the doctor’s effort to improve the patient’s asymmetric information problem on the patient’s medical care use, and the effect of the doctor’s payment method on her level of effort. The conclusion follows in Section VI.
When a person feels sick, he evaluates his health state based on a priori relevant health information. So if he finds his health state below the threshold level, he visits the doctor. The threshold health level is thought to be determined by his health information, preferences, income, and the full price of medical care (Lee, 1995). This view comes from both Dranove (1988) and Lee (1995) in that the patient’s decision-making with respect to consulting a doctor is based on his subjective evaluation of his health state given his health information and socioeconomic factors. In this study therefore, we employ those preceding models with modification and development.
When the patient visits the doctor he receives objective health information about: his health state, any necessary medical treatment for enhancing his health state, and the effectiveness of it. Based on the new information delivered by his doctor, the patient makes a decision on whether to comply with the doctor’s recommended medical treatment. If the patient agrees with the doctor, the medical care will be consumed.
In this process, at the pre-visit stage, information on his health state would affect his decision to visit a doctor by affecting the patient's determination of the threshold health state level, and at the post-visit stage, the information about the quantity of medical care needed and the effectiveness of it, would affect his decision making of whether to comply with the doctor’s recommended amount of it (Dardanoni & Wagstaff, 1990).
In this paper, we focus on the latter part of the health information effect. This means we exclude the other source of a patient’s asymmetric information problem, related to the patient’s assessment of his health state, by assuming that the patient's uncertainty about diagnosing his health state is non-existent. This assumption will be discussed later by modifying the health production functions perceived by the patient and doctor.
Let the health state of a representative person be expressed by a random variable s ∈ [0, ∞) , with s assumed to have the cumulative density function F(s) and the probability density function f(s) .
An individual’s utility function is given in Equation (1), which is assumed to be an additively separable function of his health, H , and the composite good, X whose price is assumed to be unitary. We can write an individual’s utility function as follows:
where a is regarded as an individual’s weight on health.
The individual’s budget constraint is given by Equation (2), and we consider that he has health insurance which has an actuarially fair premium, P, and which has a coinsurance rate of c, where 0 ≤ c ≤ 1 , and zero deductible. The price of per unit of medical care (M) is given by PM, so the patient’s out-of-pocket payment per medical care will be cPM. The income given to this person is Y.
The health production function that shows the relationship between the health outcome and medical care expressed in Equation (3).
T represents the effectiveness of medical care (M). Equation (3) is a specific function that Lee (1995) used in his model and we will use this type of quadratic function which implied that the marginal enhancement of health could be negative beyond a certain level.
Considering the patient’s asymmetric information problem, when the potential patient decides whether to visit the doctor, the potential patient might have an expected health outcome based on the following health production function:
At the pre-visit stage, considering the asymmetry of information between patient and
doctor, the effectiveness of treatment the patient will perceive (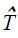 ) might be different from the doctor's one (T), because the potential patient has not yet had the chance to obtain the information
on the effectiveness of medical treatment from the doctor. Furthermore, we assume
that, at the pre-visit stage, the needed quantity of medical care for enhancing the
potential patient’s initial health state is regarded as a fixed quantity of
) might be different from the doctor's one (T), because the potential patient has not yet had the chance to obtain the information
on the effectiveness of medical treatment from the doctor. Furthermore, we assume
that, at the pre-visit stage, the needed quantity of medical care for enhancing the
potential patient’s initial health state is regarded as a fixed quantity of 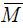 irrespective of his initial health state because it seems difficult to expect the
potential patient to have exact knowledge and information about the pattern and quantity
of medical care needed for his health enhancement.2 However, once the patient decides to visit the doctor, the quantity of medical care
will be recommended by the doctor, and the patient will decide whether to comply with
the doctor's recommendation, so we can think that the quantity of medical care will
remain to be determined at the patient's post-visit stage.
irrespective of his initial health state because it seems difficult to expect the
potential patient to have exact knowledge and information about the pattern and quantity
of medical care needed for his health enhancement.2 However, once the patient decides to visit the doctor, the quantity of medical care
will be recommended by the doctor, and the patient will decide whether to comply with
the doctor's recommendation, so we can think that the quantity of medical care will
remain to be determined at the patient's post-visit stage.
Based upon this setting, at the pre-visit stage, the potential patient determines the threshold for visiting a doctor (z*) by comparing the utility of visiting a doctor with that of not visiting a doctor, as follows.
So, the threshold for health state, z*, will be
where UNV is the potential patient’s utility of not visiting a doctor, and UV is potential patient’s utility of visiting a doctor, and pM3 is the price of 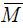 . The occurrence of a health state below his determined threshold health state would
lead him to visit a doctor, at which point he would become a real patient.
. The occurrence of a health state below his determined threshold health state would
lead him to visit a doctor, at which point he would become a real patient.
At the post-visit stage, the patient's subjective evaluation on the effectiveness
of medical care will be updated, using the information regarding this treatment that
he received from his doctor (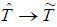 ). A patient’s subjective perception of the effectiveness of medical care however,
might be different from the true one which is held by his doctor4.
). A patient’s subjective perception of the effectiveness of medical care however,
might be different from the true one which is held by his doctor4.
Given his health state s < z* , the patient's utility at the post-visit stage will be expressed in Equation (7) below:
Based on his optimization process at the post-visit stage, the patient will determine the optimal demand for medical care. Solving this optimization problem, we can get the first order condition (FOC) as follows:
If we solve the FOC and take the expectation over s, conditional on s < z*, then we could obtain the optimal level of demand for medical care as follows:
Regarding on the interpretation of S, S is the patient’s conditional expected value of health state given it is at most z* which is his optimal threshold level of health state determined at pre-visit stage. Clearly, if a patient visits a doctor with his realized initial health, then the demand for medical care should be based on the realized value of his initial health state. However, if we consider the randomness of the patient's initial health state, it seems plausible to regard the patient's initial health state as the conditional expected value of health state. On the other hands, this view could be also interpreted by the fact that the demand for medical care shown at (9) is regarded as the one that an average patient will demand, which has been adopted in previous research, such as Lee (1995).
In this paper, the doctor is assumed to be not only an agent of her patient, but also a self interested medical care provider, which means a doctor is concerned with the enhancement of her patient’s health state after the visit, and is also concerned about her financial benefit from providing patient with medical care (Blomqvist, 1991; Rochaix, 1989). We can infer that, through the health production function (H) mentioned in the patient’s decision making process, a doctor evaluates the patient’s health benefit.
The doctor’s financial gain is represented by the profit function (Π). In order to define the doctor’s profit function, we need to describe the doctor’s revenue structure. The doctor’s total revenue from supplying M units of medical care is measured by L + (1 − r)pMM, where L is the lump-sum payment part and r is the rate of supply side cost sharing. So, out of total payments from the patient and the insurance company (pMM), a doctor could get the lump-sum payment and the rest of the total payment, except for the supply side cost sharing part, which is rpMM. So, the significant features of the doctor’s payment method are captured by L and r.5 The unit cost of providing medical care is denoted by k, which is taken to be constant for providing medical care. Based on the doctor’s total revenue and cost, the doctor’s profit function is derived as follows:
Now, the doctor’s utiltiy function (V) could be defined and be assumed to be additively separable:
The parameter b is defined as the doctor’s weight on the patient’s health benefit out of her total
utility. As seen in doctor’s utility function, in this paper, we assume a doctor cares
about the gap being close between herself and patient in terms of perception of the
effectiveness of medical care, which is represented by 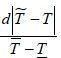 . The method of expressing the gap mentioned above will be discussed further later.
The rationale for this modification is that a doctor might be concerned about her
patient’s subjective perception of the effectiveness of medical care, because it can
play a role in formulating patient’s demand for medical care as expressed in Equation
(9). So, when a doctor recommends the amount of medical care needed to enhance the
patient’s health state, if the gap becomes larger, a doctor’s utility can be harmed
since the possibility of the doctor persuading her patient in terms of the amount
of medical care will decrease. The function G(e, M) represents the doctor’s cost of providing effort to correct the patient’s asymmetric
information problem. It is natural to think that the doctor should bear the cost from
providing this level of effort, which would have some form of financial or psychological
cost (Ma and McGuire, 1997). We assume this in the following function, Ge > 0, GM > 0, GeM > 0, Gee > 0 , which represents the cost of providing effort and shows the convexity and that
the marginal cost of providing effort can be affected by the amount of medical care
provided.
. The method of expressing the gap mentioned above will be discussed further later.
The rationale for this modification is that a doctor might be concerned about her
patient’s subjective perception of the effectiveness of medical care, because it can
play a role in formulating patient’s demand for medical care as expressed in Equation
(9). So, when a doctor recommends the amount of medical care needed to enhance the
patient’s health state, if the gap becomes larger, a doctor’s utility can be harmed
since the possibility of the doctor persuading her patient in terms of the amount
of medical care will decrease. The function G(e, M) represents the doctor’s cost of providing effort to correct the patient’s asymmetric
information problem. It is natural to think that the doctor should bear the cost from
providing this level of effort, which would have some form of financial or psychological
cost (Ma and McGuire, 1997). We assume this in the following function, Ge > 0, GM > 0, GeM > 0, Gee > 0 , which represents the cost of providing effort and shows the convexity and that
the marginal cost of providing effort can be affected by the amount of medical care
provided.
As mentioned above, due to the patient’s asymmetric information problem, it seems rational to suppose that there is a discrepancy between the patient’s and doctor’s perceptions as to the effectiveness of medical treatment. Therefore, the health production function perceived by doctor will be different from the one perceived by patient, and is expressed as follows:
In the health production function recognized by the doctor, she perceives that her patient’s initial health state is the patient’s conditional expected value of health state, S. This indicates that the patient's conditional expected value of initial health state, which denotes the average patient’s initial health state, is regarded as the same one that the doctor medically diagnoses. Hence, this setting satisfies the assumption that the patient's uncertainty in medically diagnosing his health state does not exist.
In terms of interpreting and evaluating the effectiveness of medical care, there will be a difference between the patient and the doctor. In this part, this specific aspect of asymmetric information between them will be introduced, based on the method that Lee (1995) takes in his paper. The same medical care might cause different results and these variations cannot be easily explained by epidemiological factors. Hence, a doctor’s perception (T) as to the effectiveness of medical treatment could be expressed by as follows:
where (T) represents a good outcome, and a bad outcome is expressed by (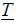 ). So, from the expression (13), we can denote λ as the statistical figure which shows the intrinsic uncertainty on the effectiveness
of medical treatment. The patient’s subjective evaluation on the effectiveness of
medical treatment could be formed by a similar mechanism as the doctor’s case. Given
this information and his own experiences, the patient would subjectly perceive the
effectiveness of medical treatment, which causes him to form
). So, from the expression (13), we can denote λ as the statistical figure which shows the intrinsic uncertainty on the effectiveness
of medical treatment. The patient’s subjective evaluation on the effectiveness of
medical treatment could be formed by a similar mechanism as the doctor’s case. Given
this information and his own experiences, the patient would subjectly perceive the
effectiveness of medical treatment, which causes him to form 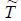 as follows:
as follows:
Thus, a patient considers T and 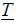 as the feasibility range of medical care, and based on the information about them,
he will construct his own probability of a good result being realized (
as the feasibility range of medical care, and based on the information about them,
he will construct his own probability of a good result being realized (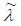 ). Hence,
). Hence, 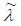 could show the patient’s specific way of interpreting the information on T,
could show the patient’s specific way of interpreting the information on T, 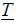 , and λ. The patient’s process of forming
, and λ. The patient’s process of forming 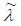 might depend on his own medical history including his own experiences of his doctor’s
practice of medicine, and his other socio-demographic factors. If we substract T from
might depend on his own medical history including his own experiences of his doctor’s
practice of medicine, and his other socio-demographic factors. If we substract T from 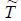 , we will have the following equation:
, we will have the following equation:
The difference between the patient’s and doctor’s perception of the effectiveness
of medical care is composed of two factors. The first factor is the difference between
the patient’s subjective method of interpreting medical information about the effectiveness
of medical care, and the doctor’s medically objective and scientific interpretation
of it, which is denoted by 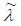 − λ. The second factor is the intrinsic uncertainty in medicine, which is denoted by
T −
− λ. The second factor is the intrinsic uncertainty in medicine, which is denoted by
T − 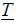 .
.
Given the intrinsic uncertainty of medicine, the method of reducing perceptional difference
between the patient and doctor is through changing the patient’s way of interpreting
medical information so that it comes to resemble doctor’s one. As shown above, 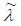 represents the patient’s specific way of interpreting the medical information on
λ, T and
represents the patient’s specific way of interpreting the medical information on
λ, T and 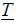 . So, in the process of the patient’s forming
. So, in the process of the patient’s forming 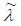 , the patient’s misinterpretation of the information delievered by doctor might be
caused by ineffective communication with his doctor. Hence, a doctor’s effort to effectively
communicate with her patient and to convey appropriate and updated medical information
to her patient might be regarded as a technique for correcting the patient’s asymmetric
information problem.6
, the patient’s misinterpretation of the information delievered by doctor might be
caused by ineffective communication with his doctor. Hence, a doctor’s effort to effectively
communicate with her patient and to convey appropriate and updated medical information
to her patient might be regarded as a technique for correcting the patient’s asymmetric
information problem.6
Therefore, from Equation (15), given T and 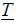 , |
, |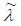 − λ|, which represents the patient’s degree of bias at interpreting medical information
on the effectiveness of medical care, might be understood as a decreaseing function
of e, which is the doctor’s effort:
− λ|, which represents the patient’s degree of bias at interpreting medical information
on the effectiveness of medical care, might be understood as a decreaseing function
of e, which is the doctor’s effort:
Since λ is drawn by medically objective results, it is natural to assume λ to be constant and close to the true value. Hence, Equation (16) could be rewritten as follows:
Besides, considering the law of diminishing marginal returns, we assume the second
derivative of 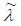 with respect to doctor’s effort level is positive, as follows:
with respect to doctor’s effort level is positive, as follows:
By using the health production function perceived by doctor, Equation (12), and the doctor’s profit function, Equation (10), we can rewrite her utility function as follows:
So, in order to get the doctor’s optimal supply amount of medical care and effort, if we solve this optimization problem, we will have the following FOCs:
Hence, the doctor’s utility maximizing amount of medical care supplied, Ms, will be obtained by solving the FOC (19), and it will be as follows:
where β = [1 − b]/b.
Concerned the optimal level of doctor’s effort which is shown at equation (20), the second term of it is interpreted by marginal cost of providing her effort and the first term of it has the meaning of the level of a patient’s upwardly biased perception on the effectiveness being corrected. If we consider that the doctor’s effort is supposed to be valuable in that a doctor might easily induce her patient to comply with the recommend amount of medical service consumed, the first term might be interpreted as the marginal benefit of providing a patient with a doctor’s effort. Hence, the eqution (20) suggests that the doctor’s optimal level of effort is determined at the point where marginal benefit and cost reach the equality.
To obtain the equilibrium quantity of medical care, we need to firstly review the process for reaching the equilibrium state. Based on the patient and doctor’s optimization processes, the equilibrium state of patient’s use of medical care can be described as follows. When a patient visits a doctor, a doctor recommends the amount of medical care needed and provides some level of effort to her patient in order to clinically persuade her patient by way of effectively communicating with him, which can correct the patient’s asymmetric information problem.
Once the patient observes his doctor’s level of effort, then the patient formalizes his own perception of the effectiveness of medical care, and based on this determines his optimal demand amount of medial care. After determining his demand amount of medical care, the patient will determine whether to comply with the doctor’s recommended amount of medical care. So, if the patient’s demand for medical care is greater or less than the doctor’s recommended amount of medical care, then the patient won’t comply with the doctor’s recommendation, which means there is no medial care purchased by the patient, and this patient might decide to visit another doctor or not to consume medical care at all.
Hence, at the equilibruim state of the patient’s use of medical care, the condition of Md = Ms should be satisfied and additionally, this condition represents that the patient complies with the doctor’s recommended amout, and that the doctor’s recommended amount is realized to be a real purchased amount of medical care at equilibruim state (Jelovac, 2001).
Based on this condition, the equilibrium price of medical care, 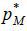 , would be determined as follows:
, would be determined as follows:
And for non-negative price,
Inserting 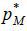 in Equation (9) or (21), we get the equilibrium quantity of medical care,
in Equation (9) or (21), we get the equilibrium quantity of medical care,
M* :
In evaluating the efficiency of the equilibrium quantity of medical care (M*), we will show that if M* is greater than the medically adequate quantity (MA) given as follows, then the patient’s use of M* cannot be regarded as the optimal state:
MA represents the amount of medical care which maximizes the patient’s health state considering the features of the health production function adopted in this paper.
In the situation where the patient shows over-consumption of medical care (M* > MA), then, from (24), we can have the following condition:
Also, we can rewrite (26) as follows:
Equation (27) can be easily proved using GM > 0 .
From Equation (27) therefore, we can see that the patient's upwardly biased belief of the effectiveness of medical care plays an important role in inducing the patient to overuse more medical care than the medically adequate quantity. Considering Equation (15) which represents the gap between patient and doctor in terms of perceiving the effectiveness of medical care, the result of (27) indicates the following:
The result of Equation (15)′ can then be revised as follows:
indicating that as a doctor increases her effort level the patient’s overestimated evaluation of the effectiveness of medical care will be reduced.
In the situation where a patient shows overutilization of medical care, the patient’s marginal utility of consuming medical care will be drawn by taking the first partial derivative of his utility function. If we put the equilibrium price and quantity of medical care expressed in Equations (22) and (24) respectively into his marginal utility, then it will be negative.7
Equation (29) implies that if the patient purchases more medical care than the medically adequate quantity, his utility will be reduced as he uses medical care. This result can be supported by the following two rationales. If the patient consumes medical care greater than MA, the patient’s health state will be exacerbated because the patient’s marginal enhancement of his health from additional consumption of medical care would be negative, and his reduced budget leads him to purchase less composite goods. Furthermore, Equation (29) indicates that the patient’s asymmetric information problem is the reason of patient’s inefficient use of medical services which also causes his utility loss.
And from the doctor’s utility function, we can calculate the doctor’s marginal utility of providing medical care, which will be zero.8
From Equation (30), we can see that even if the deterioration of her patient’s health by providing more medical care than the medically adequate quantity is a factor in decreasing her utility, the increased profit of providing more medical care could compensate for her reduced utility. Additionally, we find the asymmetry of information between the patient and doctor, which was a source of patient’s utility loss, cannot be a problem for the doctor because the doctor does not have the asymmetric information problem that the patient has.
Therefore, based on the result of Equations (29) and (30), if the equilibrium quantity of medical care is greater than the medically adequate quantity, the patient’s utility will decrease whilst the doctor’s is unchanged. This suggests that this situation cannot be regarded as the optimal state. Therefore, if we consider that this result is caused by the patient’s upwardly biased perception of the effectiveness of medical care, the patient's asymmetric information problem is the source causing the inefficient state.
Furthermore, in the case where M* is lower than MA, which is casued by the patient’s downwardly biased perception of the effectiveness
of medical care, we can easily prove 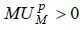 .
.
Hence, the inefficiency of patient’s consumption of medical service might originate from his information problem; over or under evaluation of treatment effect of medical services.
Based on the doctor’s payment system mentioned above, the characteristics of a doctor’s payment method could be expressed by the lump-sum payment (L), and the rate of supply side cost sharing (r) . Hence, depending on the value of L and r, we can express a specific form of the doctor’s payment method. In this paper, we will especially focus on the rate of supply side cost sharing (r) . The doctor’s rate of supply side cost sharing represents the doctor’s financial burden from her patient’s medical cost.
We can see that the doctor’s financial burden from her patient’s medical cost varies with the amount of medical care provided, while the lump-sum payment is determined at a fixed level irrespective of the amount of medical care. So, it is plausible to infer that the doctor’s rate of supply side cost sharing might affect her marginal revenue of providing the medical care, which directly affects the doctor’s marginal profit.
In terms of the doctor’s profit situation, based on the doctor’s profit function, the doctor’s marginal profit of providing medical care will be expressed by [(1 − r)pM − k]. The effect of the doctor’s supply side cost sharing on her marginal profit, holding effort and medical care constant, can be analyzed by taking the partial derivative of [(1 − r)pM − k] with respect to her rate of supply side cost sharing:9
Hence, we can see that raising the doctor’s rate of supply side cost sharing, holding e and M constant, would reduce the doctor’s marginal profit. Therefore, there would be no incentive for the doctor to increase her patient’s amount of medical care use, in terms of her own profit if the doctor’s rate of supply side cost sharing was to rise.
Furthermore, in terms of the patient’s expected health state after using the medical care, a doctor would have an incentive to try to reduce the amount of medical care purchased by her patient. As mentioned earlier, according to the health production function perceived by a doctor, if a patient consumes more medical care than the medically adequate quantity, the patient’s marginal enhancement of health state by using additional medical care would be negative, as shown in Equation (32) below:
So, the patient’s use of an additional unit of medical care would cause his health state to deteriorate. Hence, considering that the patient’s health state is one of the components in determining a doctor’s utility, the aggravation of the patient’s health state would cause the doctor’s utility to be reduced. So, there is no reason for a doctor to recommend her patient to use more medical care if her patient already overuses medical care.
Therefore we can infer that if the doctor’s rate of supply-side cost sharing rises,
a doctor may try to reduce the quantity of medical care used by her patient. However
even if a doctor intends to reduce her patient’s medical care use, a decrease in the
patient’s medical care use can be possible only if a patient complies with the doctor’s
intent of reducing the amount of medical care purchased by her patient. In the doctor-patient
interaction, a doctor would recommend less amount of medical care than before in order
to achieve her intent. So, in order to encourage the patient’s compliance with her
recommended reduced amount of medical care, a doctor needs to clinically persuade
her patient and this persuasion can be made possible by making her patient’s demand
for medical care be close to her recommended amount.10 As shown earlier, the patient’s upwardly biased subjective perception of the effectiveness
of medical care, (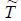 ), would increase the patient’s demand for medical care. Hence, a doctor’s effort
will decrease the patient’s upwardly biased effectiveness of medical care as follows:
), would increase the patient’s demand for medical care. Hence, a doctor’s effort
will decrease the patient’s upwardly biased effectiveness of medical care as follows:
Therefore, if the patient’s demand for medical care is reduced by the doctor’s sufficient effort, the doctor’s recommended quantity of medical care (which is lower level than before due to the rise in her supply-side cost sharing) would be more easily accepted by a patient because the patient’s demand amount would be close to the doctor’s supply amount of medical care. So with the increase in the doctor’s rate of supply-side cost sharing, if the doctor succeeds in clinically persuading her patient in terms of the desired amount of medical care use, this phenomenon means that the doctor has increased her effort level. However, if the doctor does not succeed in achieving her intent of reducing the amount of her patient’s medical care use, we can expect that the doctor’s effort level has not been increased or even decreased in spite of the rise in the doctor’s rate of supply side cost sharing.
In order to prove the notion above, on the doctor’s clinical persuasion of her patient, the comparative statics analysis can be performed based on the following two identity equations. The first identity equation is the doctor’s first order condition with respect to the doctor’s effort level below:
Equation (24)′ below, which represents the patient’s equilibrium quantity of medical care, should be used as the second identity equation.
Totally differentiating Equations (20) and (24)′ and arranging them through matrix form will give the following:
Where
So, using the Cramer’s rule, the effect of the rate of doctor’s supply-side cost sharing on the patient’s equilibrium quantity of medical care will be expressed by
where |H| is the determinant of matrix H, which is represented as follows:
As shown in (37), the sign of 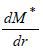 is the same as that of |H| since A < 0,
is the same as that of |H| since A < 0, 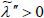 , and Gee > 0 .
, and Gee > 0 .
Depending on the sign of |H|, we can represent the two situations where the doctor succeeds or fails in persuading her patient. In the situation where the doctor faces the rise of her rate of supply-side cost sharing, her success in clinically persuading her patient in terms of reducing the amount of medical care use will be represented by applying the assumption of |H| < 0. Furthermore, in this situation, we can expect the rise of the rate of doctor’s supply-side cost sharing to induce the doctor to increase her level of effort, which means the rate of doctor’s supply-side cost sharing, would have a positive effect on her effort level.
Based on the same logic, the situation where the doctor fails in drawing her patient’s compliance with the reduced amount of medical care use will be expressed by taking the assumption of |H| > 0 . Furthermore, in this situation, we can expect the opposite case where the rise of the rate of doctor’s supply-side cost sharing would have a negative effect on her effort level.
The effect of the rate of doctor’s supply-side cost sharing on the doctor’s effort level will be expressed as follows
As mentioned earlier, if the doctor’s intent to reduce her patient’s use of medical care is achieved, the assumption of |H| < 0 would be applied for determining the sign of (37). When the assumption of |H| < 0 is applied, we can see that the sign of (38) would be positive because the part A is negative and GeM* is positive. So the internal consistency of this comparative static analysis is guaranteed as we expect.
However, if the doctor cannot succeed in reducing the amount of her patient’s medical care use, this indicates the assumption of |H| > 0 is applied and the sign of (38), as we expect, turns out to be negative. And this fact suggests that the doctor’s effort level has not increased but even decreased in spite of the rise of her rate of supply-side cost sharing, which can be regarded as the reason for a doctor’s failure in clinically persuading her patients.
Therefore based on the reasoning above, we can see that the rise of a doctor’s rate of supply-side cost sharing would induce the doctor to increase her effort level in order to achieve her intent to reduce her patient’s use of medical care. Additionally, we can see that the doctor’s effort can be regarded as the doctor’s tool for clinically persuading a patient to reduce their amount of medical care.
This paper investigated that under the newly modeled asymmetry of information existing between a patient and doctor, the doctor’s effort to correct a patient’s asymmetric information problem could enhance the efficiency of the patient’s medical care use, and that the doctor’s payment method could induce doctor to provide sufficient level of effort. Furthermore, as a policy tool that may induce a sufficient level of effort from the doctor, this paper considered the doctor’s payment method. Specifically, the doctor’s rate of supply-side cost sharing, which is supposed to represent the doctor’s payment method in this paper, is theoretically confirmed to be an effective tool, based on its desirable effect on doctor’s effort level.
Compared with previous researches, this paper might contribute the followings to the relevant research issues. Firstly, based on the revision of the patient’s asymmetric information problem, this paper found that a doctor’s practicing behavior, especially a doctor’s effort towards effective communication with the patient, can affect a patient’s asymmetric information problem, so in turn it might enhance the efficiency of patient’s medical care use. Secondly, this paper added up a new mechanism of the effect of doctor’s payment method on patient’s s decision on medical care use by clearly showing that the doctor’s effort level mentioned above might play a medium’s role in that process. Finally, in order to control rapidly increasing medical costs, previous researchers have suggested supply-side policy approaches, such as the control of the doctor’s payment method, as desirable policy tools. The clear mechanisms of its suppressing medical costs, however, have not clearly been discussed. But this paper showed that the prospective payment method might reduce the patient’s medical care use by verifying that the prospective payment method derives the optimal level of doctor’s effort of effectively communicating with her patient who is prone to overutilize medical care. Specifically, assuming that a patient’s compliance with his doctor’s recommendations for medical care is essential to the process of medical care use, this paper suggests that when the doctor faces a rise in her rate of supply-side cost sharing, a doctor has an incentive to provide sufficient effort in order to achieve her patient’s compliance with her intent of reducing the amount of medical care purchased by patient, which causes the patient to reduce medical care use. Therefore, this paper may shed some light on the likely effects of supply-side policy approaches, by detailing the effects on the doctor’s practice behavior in dealing with the patient’s asymmetric information problem.
Nowadays, Korea faces the issue of rapidly increasing medical costs, and many scholars have suggested supply-side policy approaches, such as the prospective payment system as the solution of this problem. As a part of prospective payment system, NHIC (National Health Insurance Corporation), a Korean public health insurance agency is contemplating to adopt global budgeting as of 2012. Under this payment scheme, as shown in this paper, since medical providers are responsible for the medical cost over the global budget, medical care providers will be more conscious of cost so that they will exert themselves to supply medical care services more efficiently. In other words, with the patients who want to overutilize medical care service due to his overestimation of the marginal health enhancement effect of it or due to moral hazard, it is natural for a doctor to have the intent of reducing this patient’s medical care use, so it is also natural to think a doctor would try her best for correcting her patient’s upwardly biased evaluation on the treatment effect of medical care. Hence we can expect the communication between doctor and patient might become more effective, which causes the efficiency of patient’s medical care use to be ameliorated. Therefore, the results of this paper might be utilized as an evidence of supporting that the global budgeting might induce a doctor to provide optimal amount of medical care services.
At the very same time, however, it can lead to decrease in medical care amounts supplied along with somewhat lowered service quality and longer patients’ waiting time in the way of cost-saving activity without an appropriate quality monitoring system on the medical practices. Furthermore, it may also cause difficulties in patients’ seeking proper and sufficient information on the medical care. In terms of the reconciliation of patient’s asymmetric information problem discussed above, a successful landing of global budgeting scheme should require a reliable and effective monitoring system on the medical practices.
Concerning the limits of this paper which should be explored in the future, the other source of patient’s asymmetric information problem which is concerned with patient’s health status was not dealt with this paper. And additionally, even if this paper tried to investigate the situation of patient’s over-perception of the effectiveness of medical services, the opposite situation where a patient under-evaluates it, should be analyzed for clearly suggesting the policy effect of doctor’s rate of supply-side cost sharing on her level of effort for correcting patient’s information problem.
Appendix A: Proof of [pM − (1 − r)∂pM / ∂r] ≥ 0
The sign of [pM − (1 − r)∂pM / ∂r] could be investigated by using (A-1), which represents the price of medical care at equilibrium, and the partial derivative of the price of medical care with respect to the doctor’s supply side cost sharing as follows:
The sign of (A-2) is guaranteed by using the condition of avoiding non-negativity of price of medical care at equilibrium.
So using (A-1) and (A-2), [pM − (1 − r)∂pM / ∂r] could be rewritten by as follows:
The sign of (A-3) is guaranteed still by using the condition of avoiding nonnegativity of price of medical care at equilibrium.
Appendix B: Proof of 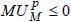
Appendix C: Proof of 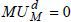
For example, if the potential patient's leg is broken, then, in pre-visit stage, he expects to wear a plaster cast if he visits doctor, because the average bone-fracture patient wears a plaster cast.
At pre-visit stage, the price of medical care is assumed to be exogenously given to
the potential patient. Based on the assumption that he expects to use  of medical care, it is reasonable to assume the price of
of medical care, it is reasonable to assume the price of  is fixed. However, at post-visit stage, the price of medical care remains to be determined
at the equilibrium state of patient’s use of medical care. Hence, the price of medical
care is regarded as be exogenous at pre-visit stage.
is fixed. However, at post-visit stage, the price of medical care remains to be determined
at the equilibrium state of patient’s use of medical care. Hence, the price of medical
care is regarded as be exogenous at pre-visit stage.
It is natural to assume that a doctor knows the true value of T, and she provides it to her patient.
For example, a capitation system can be expressed by r =1, and a complete fee-for-service system can be represented by L = 0, r = 0 , so we can see that the doctor’s reimbursement method can be broadly expressed by manipulating the value of L and r. This method is similar to Ellis and McGuire(1990).
Effective communication between patient and doctor can be possible if a doctor provides efforts at listening to a patient's various situations including medical and psychological aspects, and explaining patient's health state and effectiveness of various medical treatments in plain language (Emanuel & Dubler, 1995).
(1991). The Doctor as Double Agent: Information Asymmetry, Health Insurance, and Medical Care. Journal of Health Economics, 10, 411-432, https://doi.org/10.1016/0167-6296(91)90023-G.
, & (1990). Uncertainty and the Demand for medical care. Journal of Health Economics, 9, 23-38, https://doi.org/10.1016/0167-6296(90)90039-6.
(1988). Demand Inducement and the Physician/Patient Relationship. Economic Inquiry, 26, 281-298, https://doi.org/10.1111/j.1465-7295.1988.tb01494.x.
, & (1990). Optimal Payment Systems for Health Services. Journal of Health Economics, 9, 375-396, https://doi.org/10.1016/0167-6296(90)90001-J.
, & (1995). Preserving the Physician-Patient Relationship in the Era of Managed Care. Journal of American Medical Association, 273, 323-329, https://doi.org/10.1001/jama.1995.03520280069043.
(2001). Physicians’ Payment Contracts, Treatment Decision and Diagnosis Accuracy. Health Economics, 10, 9-25, https://doi.org/10.1002/1099-1050(200101)10:1<9::AID-HEC560>3.0.CO;2-Y.
(1995). Optimal Medical Treatment under Asymmetric Information. Journal of Health Economics, 14, 419-441, https://doi.org/10.1016/0167-6296(95)00012-7.
(1989). Information Asymmetry and Search in the Market for Physicians’ Services. Journal of Health Economics, 8, 53-84, https://doi.org/10.1016/0167-6296(89)90009-X.