I. Introduction

This paper investigates the effects of reforestation on stabilization of riverine water levels, one of the expected benefits from forests, using a panel data set from South Korea.

Forest is known to store and conserve water flow from rainfall mainly through canopy interception and soil infiltration. The canopy interception refers to water that is retained by leafs of trees and evaporates into air. Besides the canopy interception, the rainfall can be delayed in reaching soil through stemflow, which refers to water that trickles along branches. The water that reached soil can either run off as overflow or be absorbed into the underground through soil infiltration. This water-regulating function of forests is believed to contribute to preventing natural disasters such as flood and drought and enhancing agricultural productivity by steadily providing water to nearby lands.

Despite such a hydrological service and other benefits of forest to human, however, the world is continuously losing forests, especially in developing countries. According to FAO (2015), the global net loss of forests between 1990 and 2015 is 129 million hectares which is almost the size of South Africa, and the largest area of deforestation is found in South America and Africa. As Wheeler et al. (2013) among others show, deforestation is positively related to economic benefit of forest conversion to other land use in the process of economic development. According to Wheeler et al. (2013), forest clearing in Indonesian kabupatens between 2005 and 2010 was affected by economic variables such as interest rate and exchange rate. Faria et al. (2016) show that deforestation in the Brazilian Amazon between 2000 and 2010 has a positive relationship with trade openness. Li et al. (2017) further investigated the relationship between trade and forest transition with the data of nine Asian countries and reported that not only total trade volume but also trade structure affected forest transition.

Since the benefits of forest to human have externalities, however, conservationists believe that the benefits of forest protection tend to be undervalued compared to the benefits of forest conversion (Sims, 2010). As a result, conversion of forests to other land use is often made at the level higher than the optimal point. For example, when Sims (2010) compared consumption and poverty measures between localities with a high or low share of protected forest areas in Thailand, she found a positive correlation between poverty and protection. On the contrary, when a selection bias was taken into consideration in the estimation, protection turned out to reduce poverty. She explains the change in the estimation results by the ecotourism, an externality of forest. Klemick (2011) found that forest fallow significantly contributes to productivity of adjacent farms. According to the calculation of Chang et al. (2016), deforestation due to international trade caused net economic loss if the lost externalities of ecosystem is considered. Despite the increasing number of research papers exploring explicit and implicit benefits of forest to human, however, as Ferraro et al. (2012) and Tan-Soo et al. (2016) argue, our understanding of forest benefits is still quite limited.

Overall, that economic benefits from forests far outweigh costs at global and regional levels is well established beyond dispute (MEA, 2003; TEEB 2010; and Neudert et al., 2016). The main challenge in forestation and forest conservation in the developing world is that, at the local level, the benefits may fall short of the opportunity costs borne by the members of the local community (Neudert et al., 2016). Indeed, researchers based at the Korea Forest Research Institute routinely update their estimates of “nonmarket” values of the forests in South Korea. According to their most recent estimate, the positive externalities generated by the Korean forest is greater than 73 trillion won, or more than 7% of GDP, in 2008. The estimate doesn’t include the value of marketable products from the forests such as timber and some important non-market values such conservation of biodiversity. Even though the budget the Korean government allocated to promote reforestation in the 60s and 70s accounted for a fairly large portion given the size of the overall government budget, it is clear that the cumulative benefits are much larger than the initial investments at the national level.1 Thus, it should be noted that we are not conducting the current study with a view to establishing that the Korean reforestation resulted in net welfare improvement. Against this background, the present paper’s aim is quite modest: we want to demonstrate that the water storage and conservation service of the forests is real and substantial, thus contributing to the growing body of literature documenting forests’ benefits more and more rigorously.

Because Korea suffered flood damages on a routine basis due to irregular precipitation throughout its history, the South Korean government emphasized the water flow regulation function of forest to justify its national reforestation program from the initiative stage of the program expecting more stable water flow would enhance agricultural productivity and prevent flood (FAO, 2016). Even so, to our surprise, the effects of reforestation on water flow have never been scientifically investigated in the literature despite South Korea’s successful reforestation.

In fact, flood damage has decreased in South Korea for the last few decades, while agricultural productivity has increased. Figure 1 shows that the size of flooded area has substantially decreased although precipitation in summer has not at all. The average precipitation from 1973 to 1986 was 626 millimeter, and it was 765 millimeter from 2000 to 2014. However, the annual average size of flooded area has decreased between the two time periods, from 81 thousand to 23 thousand hectares. In addition, the annual average rice product per ten acre was 423 kilograms in the former time period, while it was 496 kilograms in the latter time period (see Figure 2).

FIGURE 1.

PRECIPITATION AND FLOOD DAMAGE

Source: Hydrologic Annual Report in Korea (Ministry of Land, Infrastructure and Transport), Disaster Report (Ministry of the Interior and Safety).

FIGURE 2.

RICE PRODUCTION OF SOUTH KOREA

Source: KOSIS, Statistics Annual Report of Local Government.

FAO (2016), which highly admired Korea’s reforestation, claimed the changes described above as main benefits of Korean reforestation. Seo (2018) examined the relationship between rice production and reforestation using the panel data of rice fields and adjacent forests in South Korea, and concluded that reforestation positively affected rice productivity. However, because not only reforestation but also many other factors such as construction of dams and banks and improvement in chemicals and farm machinery should also have contributed to such changes, to isolate the contribution of reforestation is not an easy task. Even so, if the water stabilization function of forest is confirmed by data, the claims of FAO (2016) and Seo (2018) will be buttressed.

In particular, this research paper collects rainfall and water level data of three Korean rivers, and examines whether and to what extent the impact of rainfall on water level of river changes as the volume of growing stock of adjacent forest grows. To the best of our knowledge, no research paper has explicitly investigated whether the impact of rainfall on water level of river declines as reforestation proceeds. In fact, only limited amount of literature has examined the impacts of change in forest such as reforestation, afforestation and deforestation on ground water flow in general.

Among those small number of exceptions, Hundecha and Bardossy (2004) demonstrated that intense afforestation reduces volume of runoff, which refers to water flows over the earth’s surface due to storm or other weather conditions with intense rainfall. The reduced runoff would delay sudden increase in water level of river and thus prevent flood. Nisbet et al. (2004) showed that planting woods along a 2.2 km grassland reach of the River Cary in Somerset of U.K could delay the water velocity and produce flood prevention effect. Cheng (1999) found that reforestation in the upper Yangtze River Valley in China led to decrease in runoff. Brookhuis and Hein (2016) showed a non-linear relationship between catchment’s forest cover and flood control in Trinidad. Also, their study estimated that the hydrological service of the forest cover is between 16 and 268 dollars per hectare per year. Tan-Soo et al. (2016) found that deforestation in Peninsular Malaysia significantly increased the number of days flooded during 1984-2000.

South Korea provides a very good natural experimental condition for this kind of study not only due to data availability but also due to its natural environment and somewhat unique economic development experience.

South Korea is located in Northern East Asia and has four distinct seasons with heavy rainfalls concentrated in summer (typically from June to August) often caused floods in near-river areas. According to FAO (2016), 100 thousand hectares was flooded and more than 150 thousand people were victimized by flood in the 1960s.

Despite the fact that seventy percent of its land is covered by forest, however, hydrological services of forest was not paid attention to in Korea until growing stock of forest got heavily lost.2 After imperialistic exploitation during the colonial times (1910 to 1945) and a three- year long Korean war (1950 to 1953), forests in South Korea were extremely devastated. According to the estimates of the Korea Forest Service, South Korea’s volume of growing stock of forest per hectare, which is a statistic that represents forest inventory, was only 6 cubic meters in the 1950s. It is just four percent of the same measure in 2015, 146 cubic meters per hectare.3 The surprising increase in the growing stock is mainly due to the efforts of the South Korean government through the National Forest Rehabilitation Plans.4

As previously stated, deforestation usually aggravates in developing countries as their economic developments progress. However, South Korea recognized the importance of forest in providing essential services for human wellbeing from the initial stage of its economic development and accomplished significant reforestation (FAO, 2016). In the 1950s and 1960s, Korea was one of the poorest countries with GDP per capita in 1960 at mere $1,175.5 However, the Five Year’s Planning of Economic Development initiated by the South Korean government in 1962 began to change the economic atmosphere of the country. Its GDP per capita rose to $10,152 in 1988, implying 12% annual growth on average. At the same time, South Korea also succeeded in reforestation. According to the Korea Forest Service, the total growing stock of forest increased from approximately 69 million m³ in 1970 to 800 million m3 in 2010.6

In contrast, according to Tang et al. (2010) and Jin et al. (2016), around 40 to 50 percent of forest area has been deforested in North Korea for the last few decades, and it is believed to be a reason for increased damages caused by natural disasters. In fact, heavy rains in August 2018 destroyed “more than 800 buildings including homes, clinics and school” in North and South Hwanghae provinces in North Korea.7 That size of flood damage is found in South Korea only in the years before reforestation. Even so, According to Lee et al. (2018), forest restoration efforts have been ineffective in North Korea for the last decade. The unique experience of South Korea which has pursued economic development and reforestation at the same time should provide useful implications for North Korea and also for countries that are in similar situation currently as Korea in the 1960s.

The following section describes the areas and rivers explored in this research. Section 3 discusses the data used in the research. In section 4, the estimation equations employed in the research and the estimation results using panel data are presented. Finally, section 5 concludes the paper.

II. Areas and Rivers Explored

Since the present research aims at investigating whether and to what extent the impact of rainfall on the water level of a river changes as the volume of growing stock of forest increases, the areas in which other factors than forest might alter the effects of rainfall on water level were excluded. Such factors include existence of a dam and major constructions to widen or deepen a river. Data availability was another consideration. Because rainfall is expected to affect water level of a river without a significant time delay, high frequency data should be desirable for this kind of research. In addition, the data of the volume of growing stock of adjacent forest must be available for a long time span. The existence of flood damage reports was also checked. Finally, the similarity of the lengths and the widths of the rivers included in the panel data was also considered. Although we control for the unobserved heterogeneity among the rivers in estimation, very large gaps in the river size would not be desirable.

After an extensive review, we finally settled on three river systems that fully satisfy the conditions above. They are the Hyeongsan River (R1), the Mangyeong River (R2), and the Hongcheon River (R3) in South Korea.8 For the three rivers, the volume of growing stock of forest in the watershed areas is reported every five year from 1985 to 2005. Besides, daily data of water level and rainfall are available for most periods from January 1, 1985 to Dec. 31, 2005.

TABLE 1

ACTUAL LOCAL AREA NAMES AND THEIR ABBREVIATED NAMES IN THE PAPER

Notes: 1) As stated in the main text, the two water level observatories in italic (R1WL4 and R2WL2) are located near the river mouth of the sea, therefore were excluded in the analysis, 2) The two rainfall observatories in italic (R2RF2 and R3RF3) were excluded in the analysis because they do not have corresponding water level observatories analyzed in the research, 3) HA is Hongcheon Agricultural High School.

Figure 3 illustrates the location of the catchment areas of the three rivers in South Korea. Figures 4 through 6 illustrate the water level and rainfall observatories in each river. There are four water level observatories and two rainfall observatories in R1. The four water level observatories are Moa (R1WL1), Angang (R1WL2), Bujo (R1WL3) and Pohang (R1WL4). The two rainfall observatories are Gyeongju (R1RF1) and Gigye (R1RF2). R1 flows through the city of Gyeongju and the city of Pohang in the Province of Gyeongsangbuk-do and flows into the sea. The basin length, which is the length from the mouth to the farthest point of the river, is 57.8 kilometers.

FIGURE 3.

WATERSHED AREAS OF R1, R2, AND R3

FIGURE 4.

WATER LEVEL AND RAIN FALL OBSERVATORIES AT R1 (THE HYEONGSANRIVER)

FIGURE 5.

WATER LEVEL AND RAIN FALL OBSERVATORIES AT R2 (THE MANKYEONG RIVER)

FIGURE 6.

WATER LEVEL AND RAIN FALL OBSERVATORIES AT R3 (THE HONGCHEON RIVER)

For R2, there are two water level observatories, Daecheon (R2WL1) and Dongjisan (R2WL2), and two rainfall observatories, Gosan (R2RF1) and Impi (R2RF2). R2 flows through the city of Wanju and the city of Iksan in the Province of Jeollabuk-do and flows into the see. Its basin length is 74.8 kilometers.

For R3, there are two water level observatories, Bangok (R3WL1) and Hongcheon (R3WL2), and three rainfall observatories, Bangok (R3RF1), Hongcheon Agricultural High School (R3RF2) and Naechon (R3RF3). R3 flows through the city of Hongcheon in the Province of GangWon-do and joins the Han River, which flows through Seoul, the capital city of South Korea. The basin length of R3 is 108.5 kilometers.

Among the eight water level observatories mentioned above, R1WL4 in R1 and R2WL2 in R2 are located near the river mouth close to the sea. Therefore, the dynamics of the sea will affect the water level significantly, obscuring the effect of rainfall or reforestation. Accordingly, the two water level observatories were excluded in the analysis. Table 2 shows the six water level observatories included in the analysis and their corresponding rainfall observatories. The corresponding rainfall observatory of a water level observatory is the one located in the nearby upper stream area of the water level observatory. Because R1WL2 and R1WL3 are related to the same corresponding rainfall observatory (R1RF2), there are six water level and five rainfall observatories included in the research as Table 2 shows. In section 4, the water level measured at each of the six water level observatories is regressed on rainfall measured at its corresponding rainfall observatory along with other explanatory variables. Through the regressions, this paper examines whether the impact of rainfall on water level has been alleviated as adjacent forest grows. The analysis of Baak et al. (2016) shows that flood damage is related more closely to water level rather than rainfall, implying to control the water level of a river is important to prevent flood. If higher volume of growing stock of forest helps to control water level, it should serve as a strong rationale for afforestation and forest conservation.

TABLE 2

WATER LEVEL OBSERVATORY AND CORRESPONDING RAINFALL OBSERVATORY

Note: 1) WL is water level observatory, 2) RF is rainfall observatory, 3) The rainfall observatory that is located in the nearby upper stream of a water level observatory is the corresponding rainfall observatory of the water level observatory.

Figures 7 through 9 illustrate the volume of growing stock of forest in each watershed area of the three rivers. The lines in the figures are log values of the volumes, therefore their slopes represent the growth rate of the volume. As seen from Figures 7, the volume in R1 watershed area was only 1.2 million m³ in 1985, but increased to 5.3 million m³ in 2005.

FIGURE 7.

VOLUME OF GROWING STOCK OF FOREST (THE HYEONGSANRIVER (R1) WATERSHED AREA)

Source: Water Resources Management Information System (http://www.wamis.go.kr/).

FIGURE 8.

VOLUME OF GROWING STOCK OF FOREST (THE MANKYEONG RIVER (R2) WATERSHED AREA)

Source: Water Resources Management Information System (http://www.wamis.go.kr/).

FIGURE 9.

VOLUME OF GROWING STOCK OF FOREST (THE HONGCHEON RIVER (R3) WATERSHED AREA)

Source: Water Resources Management Information System (http://www.wamis.go.kr/).

The volume of growing stock in R2 watershed area was 1.4 million m³ in 1985, slightly higher than that in R1 watershed area. However, since the volume grew more slowly than in R1 area, it was only 3.2 million m³ in 2000 when that in R1 area reached more than 4 million m³ . Different from the volume in R1 area whose growth slowed down from 2000, the volume in R2 area grew relatively fast between 2000 and 2005. Even so, it increased up to only 4.8 million m³ in 2005.

Different from the two watershed areas mentioned before, the volume of growing stock in R3 watershed area increased very rapidly between 1985 and 1990 as illustrated in Figure 9. It increased up to 4.9 million m³ as early as 1990, which is the level the previous two areas reached in around 2005. This rapid growth of the volume in an early stage might be explained by that R3 flows through mountainous areas. The growth rate of the volume in R3 area slowed down from 1995, but the volume was 12 m³ in 2005, more than two times the counterpart in the two previous areas.

III. Data

The water level and rainfall data used in this paper are official data from the Ministry of Land, Infrastructure and Transport of the South Korean government.9 The data for R1, R2 and R3 were provided by Nakdong River Flood Control Office, Geum River Flood Control Office, and Han River Flood Control Office, respectively. All the flood control offices are subsidiary organizations of the Ministry of Land, Infrastructure and Transport of South Korea. The measurement unit of water level is one meter, and that of rainfall is one millimeter.

Both daily and hourly data from January 1, 1985 to December 31, 2014 were obtained from the offices above. However, mainly due to the lack of measurement infrastructure before 2000s, there were substantial number of missing values especially in the hourly data. Since daily data had much smaller number of missing values than hourly data, this paper used daily data for econometric analyses in the following section. In addition, it should be reported that the data were originally hand-written by the staffs of each river flood control office, and transferred to electronic forms quite later. Therefore, erroneous or difficult-to-read handwriting records sometimes made weird numbers in the electronic data sets. For example, the water level of R1WL on March 17 was 0.664, while it is 1.664 on the previous and the following day. Because it is obviously a record mistake, it was corrected to 1.664. When the correct numbers cannot be reasonably traced, the numbers suspected to be errors were treated as missing values. One example is the rainfall data whose values were negative for 17 days in December, 1996. Although those erroneous values question the quality of the data, it should be also reported that they are much less than one percent of the whole data.10

Although the rainfall and water level data are available up to 2014, we confined the time period of our analysis to 1986-2005 (January 1, 1986 to December 31, 2005) due to two reasons. Above all, the data for the volume of growing stock of forest in each watershed area of the three rivers are available up to 2005. Besides, the Four Major Rivers Project implemented by the South Korean government between 2009 and 2011 immensely changed the landscape of the watershed areas of South Korean rivers.11 Although the three rivers included in the research were not directly affected by the project, they might be indirectly influenced. Because the factors such as construction of banks, which may alter the impact of rainfall on water level, should be controlled, it may not be wise to include the period of the Four Major Rivers Project in this kind of research.12

The water level data collected by the government offices are the data of river stage whose value is affected by the level of gage zero. “A gage zero” is an arbitrary point, which is normally set below water surface of a river at the driest season. The water level above the gage zero is called “a river stage,” and in many cases, water level observatories report only the data of river stage. Each gage zero has an elevation level above mean sea level, and the addition of the river stage and the elevation level of the gage zero is “the water level of a river above mean sea level.” Despite its convenience, river stage cannot be used for econometric analysis unless gage zero has not been changed. However, as Table 3 shows, a gauge zero in the three rivers involved in the research were changed a few times. For this reason, this study used the water level above mean sea level rather than the water level above the gauge zero. As Table 4 shows, however, the water levels above mean sea level are quite diverse across the six observatories because the altitudes of the rivers are all different. The water level above mean sea level is between 125.2 and 119.55 meters at R3WL2, and between 0.04 and 6.71 at R1WL2. Because the relative altitude of each river is not important and may add unnecessary heterogeneous noises on the estimation, the water level of each river is standardized by subtracting the minimum level from each data and adding one. Accordingly, the lowest water level in each river in the standardized data is one meter.13 The basic statistics of the standardized water level data are also reported in Table 4. Figures 10 through 15 illustrate the standardized water level and the rainfall of each observatory. The econometric analyses in the following section use the standardized data as the water level.

TABLE 3

HISTORY OF GAUGE ZERO (FROM 1985 TO 2005)

TABLE 4

BASIC STATISTICS OF THE DATA

As previously mentioned, this research chose the three rivers because they are not significantly affected by dams or major constructions to widen or deepen the river. Even so, as Figures 10 through 15 shows, the water level data of some observatories show substantial structural changes. Figure 10 shows that water level at R1WL1 is distinctively higher from 1997. In fact, the original water level data provided by the Korean government shows that water level at R1WL2 jumped from 1.985 on Feb. 10 to 2.405 on Feb. 11 in 1997 without any explanation provided, although there was no rain in that month. This jump caused a significant change in the mean value of the water level after Feb. 10, 1997. Similar unexplained change in the mean of the water level is found at R1WL2 in 2000 and at R3WL2 in 1993. In the case of R1WL1 and R1WL2, those unexplained jumps occurred after the gage zero changed. Therefore, one reasonable conjecture is that the unexplained water level changes might be caused by measurement errors due to using inappropriate gage zero.14 To deal with that problem, this paper uses dummy variables for the periods during which water level is consistently higher or lower than other periods. The dummy variables used in the estimations are reported in Table 5.

FIGURE 10.

WATER LEVEL AND RAINFALL AT R1WL1

Note: WLN=water level, meter. RF=rainfall, millimeter.

FIGURE 11.

WATER LEVEL AND RAINFALL AT R1WL2

Note: WLN=water level, meter. RF=rainfall, millimeter.

FIGURE 12.

WATER LEVEL AND RAINFALL AT R1WL3

Note: WLN=water level, meter. RF=rainfall, millimeter.

FIGURE 13.

WATER LEVEL AND RAINFALL AT R2WL1

Note: WLN=water level, meter. RF=rainfall, millimeter.

FIGURE 14.

WATER LEVEL AND RAINFALL AT R3WL1

Note: WLN=water level, meter. RF=rainfall, millimeter.

FIGURE 15.

WATER LEVEL AND RAINFALL AT R3WL2

Note: WLN=water level, meter. RF=rainfall, millimeter.

TABLE 5

DUMMY VARIABLES

As noted earlier, the volume of growing stock of forest is measured every five years by the Korea Forest Service. Therefore, daily data are not available. However, different from economic and financial data, the volume is expected to grow quite steadily even if the growth rate may not be perfectly constant. Based on that point, we obtained daily volume data by assuming a linear change in the volume throughout a year. The first observation, the data of 1985, was used as Dec. 31, 1985 data. Accordingly, the last observation, 2005 data, was used as Dec. 31, 2005 data. The volume data are available for only this period. Therefore, the time span of the research is limited to from January 1, 1986 to December 31, 2005. The measurement unit of the volume data is one billion m³ . Because the measurement units of the variables are important when we interpret estimation results, they are summarized in Table 6.

TABLE 6

MEASUREMENT UNIT OF EACH VARIABLE

IV. Panel Data Analysis

A. Estimation Results

To determine whether reforestation has contributed to stabilization of water levels of the three rivers chosen, the following equation is estimated.

where Y_it is the water level at a specific water level observatory and X_it is the amount of rainfall observed at the corresponding rain-fall measuring spot. F_it is the volume of growing stock of the adjacent forest. D_j,t is a period dummy variable to capture the effect of a structural shift in the water level possibly caused by a change in gauge zero. As summarized in Table 5, the R1WL1, the R1WL2 and the R3WL2 observatories have one period dummy for each. The term μ_i is the unobserved heterogeneity across the six cross-sections, and it ε_it is a disturbance.

Because the water level of a river should have a strongly positive relationship with its value of the previous day and because water level should not explode, α₁ is expected to be a positive number close to but less than one. Because the amount of rainfall in one area will raise the water level of a river in the same area, α₄ is expected to be positive. The coefficients, α₂ , α₃ , α₅ , and α₆ of the interaction terms, Y_it-1 F_it, 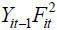, X_itF_it, and 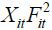will capture the impacts of the volume of growing stock of forest on water level. If the forest has the function to stabilize water level, α₂ and α₅ should be negative. The signs of α₃ and α₆ depend on whether the marginal effect of forest to control water level is diminishing or accumulating. This point will be further discussed below with the estimation results. The stationarity of all the variables included in equation (1) was examined by the panel unit root test of Levin, Lin, and Chu (2002). The null hypothesis of presence of unit root was strongly rejected for all the variables.

Table 7 reports the estimation results of equation (1) for four different models. Column 1 reports the estimates of the pooled OLS model. In column 2, dummy variables are dropped. Columns 3 and 4 report the estimates of the fixed effects model with two different specifications just as the OLS model. Because the number of explanatory variables is greater than the number of cross-sections, the random effects model could not be estimated. Since the work of Nickell (1981), it has been well known that the coefficient of the lagged dependent variable in a dynamic panel model (α₁ in equation (1)) is not consistently estimated by fixed effects or random effects models due to the endogeneity problem caused by the correlation between the lagged dependent variable and the error terms. However, as Roodman (2006) among others argues, the inconsistency is negligible if the dimension of cross-sections is far bigger than the dimension of time series, which is the case of the data in this paper. Accordingly, a methodology such as the system GMM of Arellano and Bover (1995) and Blundell and Bond (2000), which are recommended for dynamic panel data analyses when the number of cross-sections is bigger than that of time series, were not employed in the present research.

TABLE 7

ESTIMATION RESULTS (WHOLE TIME PERIOD)

Note: The asterisk indicates the estimate is significance at the 5% significance level.

The estimates of the OLS model are quite similar to those of the fixed effects model in each specification except for the estimates of dummy variables. The estimates of dummies are all insignificant at the five percent significance level in the OLS model in column 1, but they are all strongly significant in the fixed effect model in column 3. The p-value of the redundant test for the fixed effects is almost zero, strongly supporting the fixed effects model over the OLS model.

In all versions of the model, α₁ is estimated to be around 0.9, consistent with our expectation. The coefficients of the interaction terms between forest volume and other explanatory variables, α₂ and α₅ are estimated to be negative, implying that forest can contribute to controlling water level. The positive signs of α₃ and α₆ indicate that the marginal effect of forest is diminishing.

For an additional robust check, Equation (1) was estimated using only summertime data (May to October). The results reported in Table 8 show that the signs of all coefficients are the same as in Table 7, re-confirming that water level is better controlled as the forest grows, but that the marginal effect of forest to control water level diminishes.

TABLE 8

ESTIMATION RESULTS (MAY TO OCT.)

Note: The asterisk indicates the estimate is significance at the 5% significance level.

Because the forests adjacent to the three rivers explored have continued to grow for the time period covered in the paper, it is a reasonable suspect that a trend may play a similar role to the volume of growing stock in equation (1). Therefore, equation (1) was re-estimated after replacing the forest volume with a trend, and the estimation results are reported in Table 9. Although the interaction terms of trend have the same signs with respect to rainfall, their signs turn out to be the opposite, with respect to lagged water level, to those reported in Tables 7 and 8. Besides, the estimate of α₂ is not significant in Table 9. This indicates that the water-stabilization effects of forest found in the estimation of Equation (1) is not the results of some unknown time trending effects.

TABLE 9

ESTIMATION RESULTS OF FIXED EFFECTS MODELS (FOREST DENSITY IS REPLACED BY TIME TREND)

Note: The asterisk indicates the estimate is significance at the 5% significance level.

Because the test results for redundant fixed effects support the fixed effects model and because all dummies turn out significant, the simulation experiments in the following section use the estimates of the fixed effect model with dummies in Table 7.

B. Effects of Forest on Water Level: A Simulation

From Equation (1), it is obvious that the direct impact of rainfall, X_it , on the water level, Y_it , is 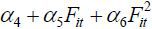. In addition, X_it also affects Y_it+1 through Y_it. That is,

By the same token, the impact of X_it on Y_it+j , or the change in the water level responding to a unit (millimeter) change in rainfall, can be also computed.

Figure 16 illustrates the simulated daily effects of rainfall on water level in two cases. The first case (Case 1) is that the volume of growing stock is one million m³ , and the second case is that it is five million m³ (Case 2). As Figures 7 through 8 show, the volumes of growing stock of the two forests in the watershed area of R1 and R2 were around one million m³ in 1985. However, they increased to around five million m³ in 2005. Therefore, the simulations in Figure 16 can be understood to compare the impacts of rain fall on water level between two rivers, one with the forest of the year 1985 and the other with the forest of the year 2005. Such a simulation will illustrate the extent to which reforestation contributed to stabilizing water level in South Korea. Specifically, Figure 16 depicts the daily changes of water level when the amount of rainfall is 100 millimeters at day 0 and there is no rain from day 1.15

FIGURE 16.

SIMULATED EFFECTS OF RAINFALL ON WATER LEVEL

When it rains one hundred millimeter per day at time zero, the water level rises by 0.70 meter on that day, if the volume of growing stock is 1 million m³ . In contrast, the water level rises by 0.48 meter, if the volume of growing stock is 5 million m³ . Then, the effects of rainfall gradually vanish.

Figure 17 illustrates the simulation applied to the case of heavy rain in R1 area. On august 22 and 23 in 1991, there was heavy rain at R1WL1, 204 and 371 millimeters, respectively, and the water level rose by around 5 meters on August 23. The economic damage of R1 area caused by flood in that year was estimated to be 0.61 billion dollars. Ten people lost their lives and 4055 people were affected. The real line shows the simulated water level using the actual forest volume of that time period, while the two dotted lines illustrate the simulated water level based on the estimation results of column 3 in Table 7. The higher dotted line is the simulation results using the actual forest volume in 1991 (around 2.2 million cubic meter) and the lower one using the forest volume in August 2005 forest volume (around 5.2 million cubic meter). When the actual forest volume was used, the water level was simulated to rise as high as 5.36 meter, while it was simulated to rise up to 4.66 meter. This implies that the water level at R1WL1 in August 1991 could have been reduced by 13% if the forest volume had been as thick as in August 2005.

FIGURE 17.

SIMULATED EFFECTS OF RAINFALL ON WATER LEVEL

V. Summary and Conclusion

The main objective of this study is to conduct an empirical analysis to test for the impact of reforestation on stabilization of water level in three Korean rivers, R1, R2, and R3. The daily data used in the empirical studies were collected from three water level observatories and two rainfall observatories at R1, one water level observatory and one rainfall observatory at R2, and two water level observatories and two rainfall observatories at R3.

The three rivers were selected because they have not been affected by dams and/or major operations to widen or deepen the rivers. In addition, data availability was also considered. The data for water level, rainfall, and volume of growing stock of forest are available in the three rivers for most of the time periods from 1985 to 2005.

In particular, this research paper regressed present water level on previous water level, present rainfall, and their interaction terms with the volume of growing stock. In the dynamic panel data analysis of six water level observatories, the coefficients of previous water level and present rainfall were estimated to be positive and significant as expected. The interaction term between previous water level and forest volume turned out to be negative, and the interaction term between present rainfall and forest volume also turned out to be negative. These findings imply that the water level is better controlled as the volume of growing stock increases. In the meantime, the interaction term between each of the two main explanatory variables and squared forest volume was estimated to be positive, implying the marginal effect of water control function of forest diminishes as the volume of growing stock increases.

When the volume of growing stock was replaced by a trend, the signs of the coefficients were different from what were previously obtained, confirming the effects of reforestation cannot be attributed to unknown time trending effects.

Simulations employing estimated coefficient values show that reforestation reduces impacts of rain on water level substantially. Specifically, when it rains one hundred millimeter per day at time zero, the water level rises by 0.70 meter on that day, if the volume of growing stock is 1 million m³ . In contrast, the water level rises by 0.48 meter, if the volume of growing stock is 5 million m³ . Then, the effects of rainfall gradually vanish.

The water level controlling function of forest may be ignored in the decision making process of development plans because the benefits may not be obvious to casual inspection, possibly contributing to trends for deforestation in the course of economic development. This paper focused on finding the econometric evidence of the water storage and conservation function of forest. Rigorous monetary evaluation of this and other positive externalities from forestation is beyond the scope of the current paper, but would contribute to a more systematic and comprehensive cost benefit analysis of reforestation interventions. It is the hope of the authors that the findings from this paper will serve to facilitate such future research efforts.