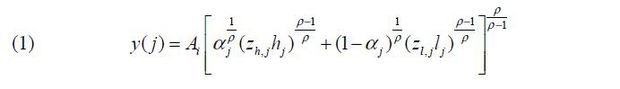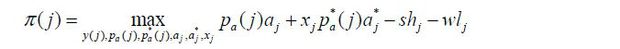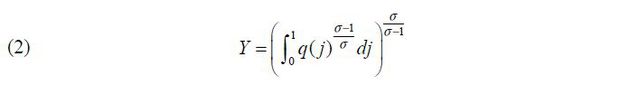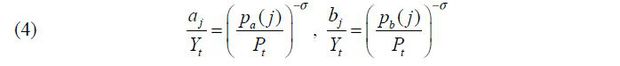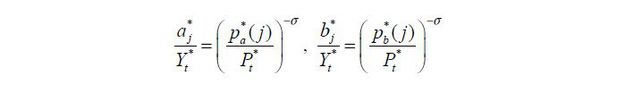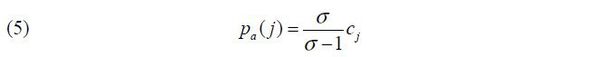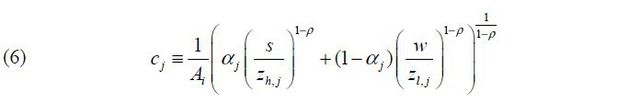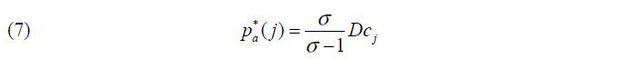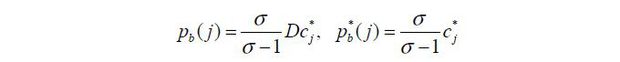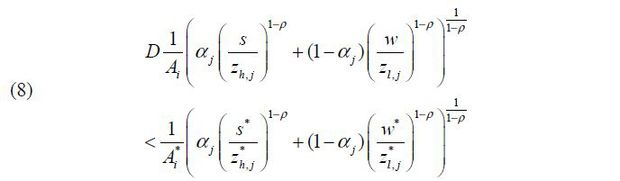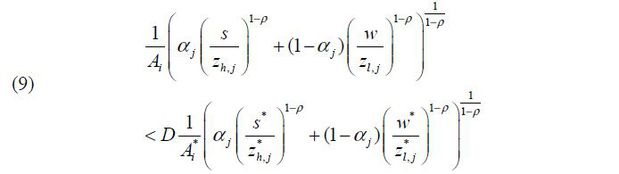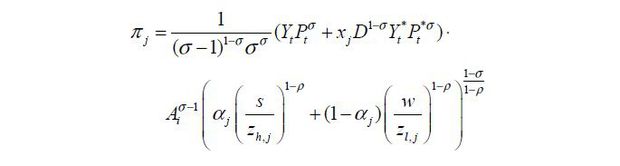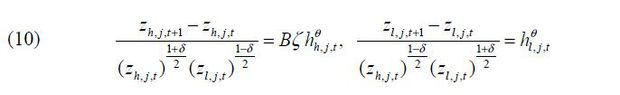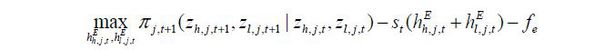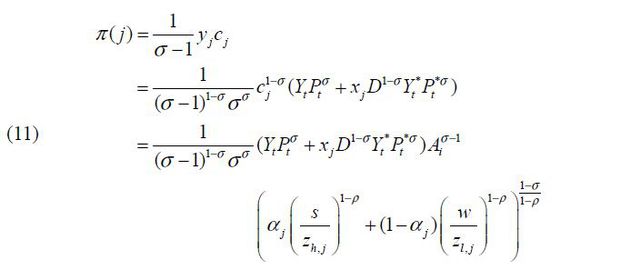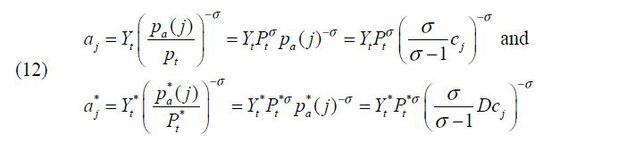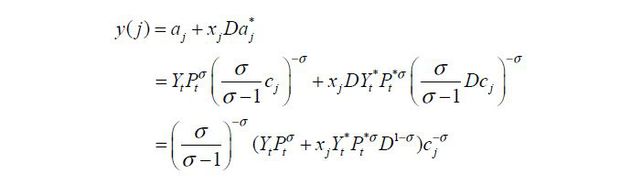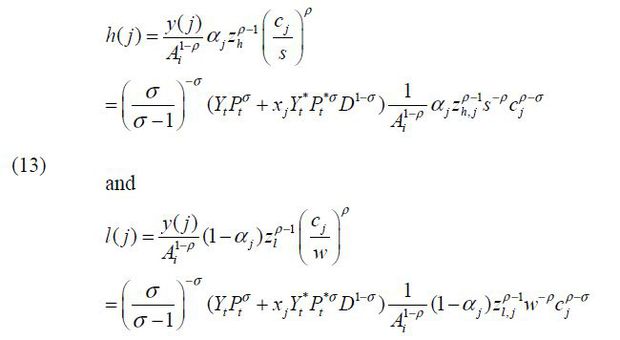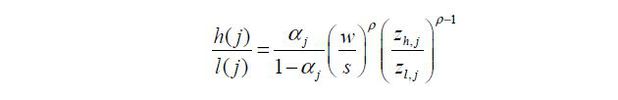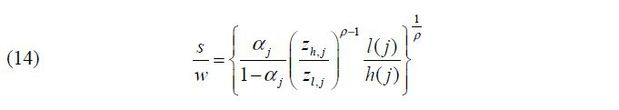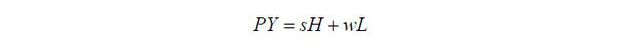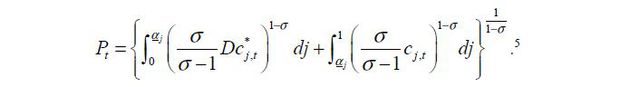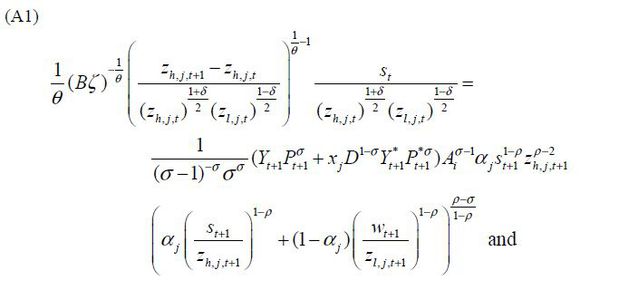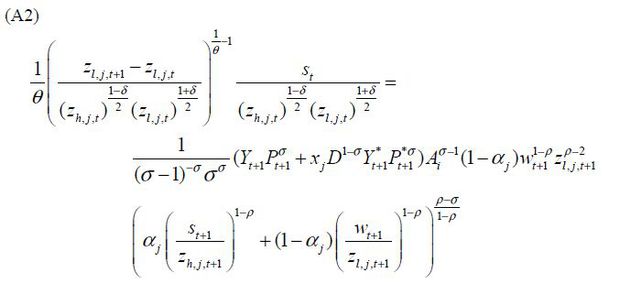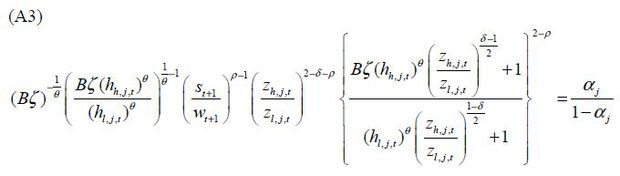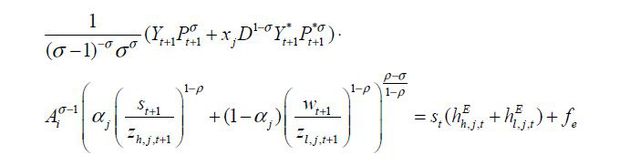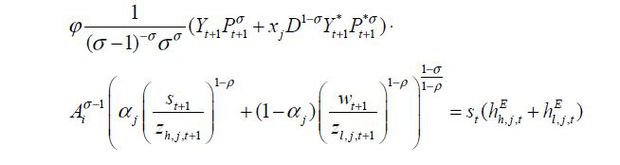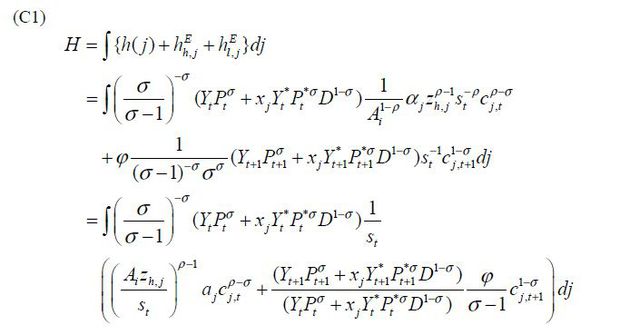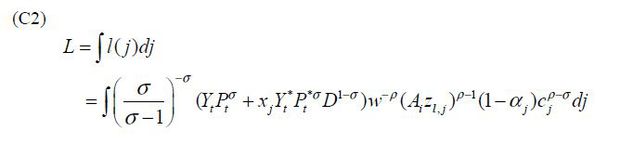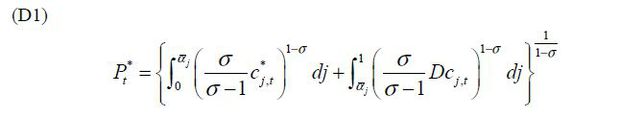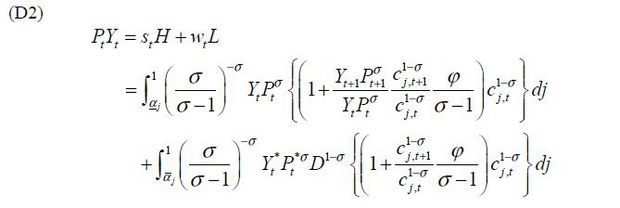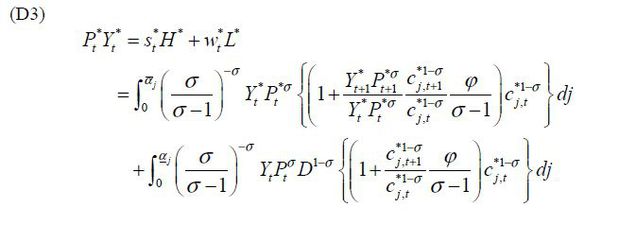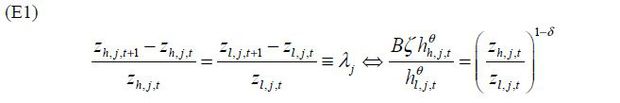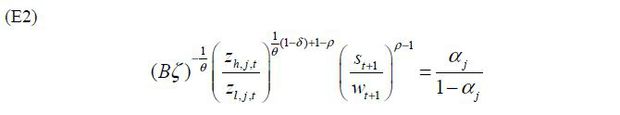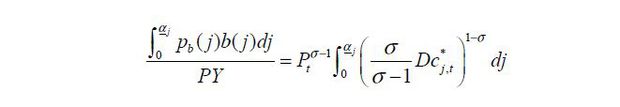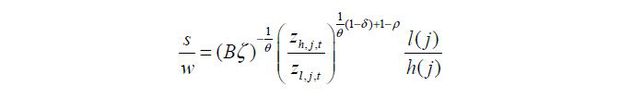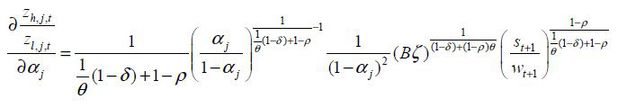International Trade and Directed Technical Change in Developing Countries†
Abstract
This paper examines the relation between the skill premium and international trade given differences in the relative supply of skills across countries while allowing the South (developing countries) to develop its appropriate technology. Typical assumptions put forward in the literature state that either technology is exogenously given, or technical change is allowed only in the North (developed countries). I present a model of international trade with endogenous growth by allowing the South to direct its technology. The results show that more R&D is directed towards skill-augmenting technology in the North than in the South, in sectors with the same skill-intensity. Technical change induced by lowering trade costs can increase the skill premium in both the North and the South. This result can explain the empirical observation that the skill premium has increased within many developing countries after they experienced trade liberalization. Finally, the model predicts larger gains from trade compared with the model where technical change is either not allowed, or allowed only in the North.
Keywords
Directed Technical Change, Globalization, Economic Growth, Skill Premium
JEL Code
F16, F43, O33, O41
I. Introduction
There is a strand of literature which attempts to explain the observed increase in wage inequality between skilled and unskilled workers within developing countries (the South) after they become more open to trade.1 However, the Heckscher-Ohlin model, a standard general equilibrium model of trade, predicts that the South will experience a decrease in wage equality since the demand for its unskilled labor, the relatively abundant factor in the South, will increase after opening to trade. This prediction is known as the Stolper-Samuelson theorem. The contradicting evidence to the prediction prompted trade economists to come up with alternative models. For example, Zhu and Trefler (2005) present a model that can yield an increase in inequality in the South depending on the rate of productivity catch-up by the South. Acemoglu (2003) develops a model by endogenizing technical change towards a particular factor (skill-biased technical change) and studies the skill premia and the direction of technical change when there is an increase in international trade. In a world economy consisting of the United States and multiple developing countries, a relatively more skill-abundant developing country can experience an increase in the skill premium when there is more trade. Acemoglu (2002; 2003) provides analyses on conditions that shape the direction of technical change. What is common in this area of literature is that technical change is performed by the skilled labor in the North, where skilled labor is relatively more abundant than the South. The South adopts the technology developed in the North. This technology, however, may not be suitable since it is developed to suit the factor endowments in the North. There is a long-standing view of technology adaptation of the North (or world) technology in the South including Parente and Prescott (1994) and Barro and Sala-i-Martin (1997).
In this paper, I argue that the South can engage in technical change and utilize their best-fitted technology to produce goods, rather than adopting technology developed in the North. This view may be more appropriate for many developing countries where the economy is not stagnant. The notion of ‘appropriate technology’ is not novel.2 Basu and Weil (1998) introduce ‘appropriate technology’ which can be developed for a given capital-labor ratio. However, the difference between countries originates from the difference in (exogenously given) saving rates which are isomorphic to productivity levels. Countries do not differ in their factor endowments and there is no international trade. The model that I present in this paper examines the relation between the skill premium and international trade while allowing the South to develop its appropriate technology, given a different relative supply of skills across countries. Acemoglu (2003) is closely related to my paper since it focuses on studying the impact of international trade on the skill premium. The key difference is that, in the Acemoglu paper, producers in the South will always adopt U.S. (the North) technology under the somewhat strong condition that their technologies are always less productive than U.S. technologies. My model allows the South to develop its own technology and, as a result, the direction of technical change in the South can be different compared to the North. This result is more in line with the “appropriate technology” literature in which countries choose disparate technologies that are more appropriate to their factor endowments.
I present a simple endogenous growth model with international trade. In the general equilibrium set up, I study how technology advancement is directed towards a particular factor of production when there is international trade between the North and the South. The North has endowed with a relatively higher fraction of skilled labor to unskilled labor than the South. Cross-country differences in factor endowments and sectoral productivities affect the incentive to invest in R&D toward each factor. The main result shows that more R&D is directed towards skill-augmenting technology in the North than in the South in the sector with the same skill-intensity. This means that the South uses unskilled labor more efficiently than the North. Trade allows the North to focus on more skill-intensive sectors not only in production but also in technology advancement. Moreover, innovation is directed toward skill-augmenting technology as the skill intensity of sector increases.
I examined the impact of trade on the skill premium. As trade costs change, there is a reallocation of resources in both production and innovation, which leads to a change in the skill premium. The skill premium in the South can increase when trade costs are lowered because the demand for skilled labor increases for R&D in technologies related to labor-intensive products. Although the result is not directly comparable to the Acemoglu (2003) paper due to differences in model specification, there is a difference in the mechanism that leads to an increase in the skill premium in the South. The South does not hire skilled labor for R&D in Acemoglu (2003). More than two developing countries should exist and their relative skill scarcity should differ enough to prompt an increase in the skill premium in the South. When trade opens up, the skill premium increases in a relatively skill-abundant developing country and decreases in skill-scarce developing countries. Another important result of my paper is that gains from trade exist not only due to specialization but also from endogenous directed technical change. This extra channel of gains from trade is closed when the technical change only happens in the North.
Several empirical studies find that the directions of technology differ as their factor endowments vary across the income-levels of the countries in question. Caselli and Coleman (2006) perform a cross-country analysis and find that lower-income countries use unskilled labor more efficiently than higher-income countries. Romalis (2004) uses detailed trade data between the United States and several other countries to analyze how factor proportions determine the structure of commodity trade. The sectors are ranked by skill intensity, which is approximated by the ratio of nonproduction workers to total employment in each industry. Alternatively, average wages can be used to measure skill-intensity. Romalis finds that the northern country has larger shares of more skill-intensive industries. Bloom, Draca, and Van Reenen (2016) have done empirical work measuring technical change by IT, patent counts and citations, and TFP. Using a panel of over to 200,000 European firms, they find a positive impact of increased Chinese import competition on technical change. The European countries included in their analysis corresponds to the North. They found that the share of unskilled workers declined with the rise in Chinese import competition. Motivated by these empirical findings, this paper gives a theoretical background on the cross-country differences in the direction of technical change toward the factors of production.
The next section presents the two-country model based on directed technical change. Section III introduces the supply side of new technology by defining the cost of technical change. Section IV characterizes equilibrium and presents an analysis of the balanced growth path (steady-state equilibrium). Section V concludes the paper.
II. The Model
There exist two countries, the North and the South. Each country shares the same production technology and utility function. The difference between the two countries lies in their endowment in skilled labor (h) and unskilled labor (l). These two are the factors of production and they are supplied inelastically. There can be initial sectoral differences in technology. There exists a continuum of sectors on [0, 1]. Sector j is arranged to rank sectors by its skilled labor intensiveness. I focus on country N in this analysis. Time subscript t is muted in the following section.
A. Production Technologies
A good in sector j is produced with the following production function:
where Ai is general technology for country i. hj and lj are the skilled labor and unskilled labor hired in sector j respectively. zh(zl) is a technology augmented to the factor h(l). Innovation is s-augmenting if there is an innovation on zh and l-augmenting if zl improves. And ρ > 0 is the elasticity of substitution between skilled and unskilled labor. αj denotes relative importance of skilled labor (e.g. if αj = 1, a firm in sector j hires only skilled labor).
The produced good will be consumed domestically and (or) be exported. And trade cost is expressed as iceberg cost where D(≥1) units should be produced in order to export 1 unit of a good. Thus, y(j) = a(j) + xjDa*(j) where a*(j) is the quantity of goods exported to country S. Certain goods are not produced but imported from country S. Goods are imported when the price of the imported good is cheaper than the price of domestically produced good.
The profit of a firm is
where pa(j) is the price of good j in domestic market and 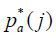 is the price of good j in foreign market. s denotes the wage paid for skilled labor while w is the wage for unskilled labor.
is the price of good j in foreign market. s denotes the wage paid for skilled labor while w is the wage for unskilled labor.
Under the resource constraints, outputs are used either in the North or the South,
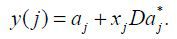 Producers maximize their profits subject to resource constraints and production technology
given by Eq. (1).
Producers maximize their profits subject to resource constraints and production technology
given by Eq. (1).
B. Demand for Final Consumption Good
A non-tradable final consumption good is produced at home and foreign intermediate goods by competitive producers using the following CES aggregate function:
The final consumption good producer purchases q(j) a quantity of goods j, which is 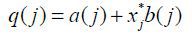 . a(j) is the quantity of goods produced and consumed within the country. b(j) is the quantity of goods produced and imported from country S. σ >1 is the elasticity of substitution between sectors. xj ∈ {0, 1} indicates whether the country exports or not for good j.
. a(j) is the quantity of goods produced and consumed within the country. b(j) is the quantity of goods produced and imported from country S. σ >1 is the elasticity of substitution between sectors. xj ∈ {0, 1} indicates whether the country exports or not for good j. 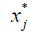 is the export decision of a firm j in foreign country. The value is 1 when the firm exports.
is the export decision of a firm j in foreign country. The value is 1 when the firm exports.
The model setup is similar to Atkeson and Burstein (2010), where each firm produces differentiated goods in a measure of operating firms. In their analysis, when a new firm enters the market, it will create new differentiated goods. Here, the new firm replaces the operating firm.
The model in this paper assumes that both skilled labor and unskilled labor are given. Innovation is directed toward the specific factor of production. A directed technology change model is introduced in Acemoglu (2002; 2003). Here, we allow the South to develop its own technology rather than importing technology developed in the North.
Moreover, there are sectoral differences in skill-intensity. Each sector has a different incentive in directing R&D to a specific technology. The model allows us to study how a relative supply of skills affects the structure of trade. The main goal is to analyze how this trade structure interacts with innovation.
C. Demand for Intermediate Goods
Final consumption good producers buy intermediate goods from home producers at prices
pa(j) and from foreign producers at prices pb(j). They will purchase cheaper good j of the two goods. Thus, the price of a good j will be p(j) = min{pa(j), pb(j)}. Consumption of intermediate goods j is 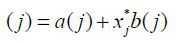 . A solution to the final consumption good producer’s problem leads to the following
demand functions:
. A solution to the final consumption good producer’s problem leads to the following
demand functions:
Price of final consumption goods is
Demand for intermediate good j is
Demand for intermediate good j in the South is
Intermediate good producers face this demand curve with elasticity σ . They charge constant markup over their marginal costs. Price of good j is
where unit cost is defined as
Export price of good j reflects trade cost:
Prices of goods in the South are
Good j will be exported when 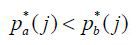 , which is
, which is 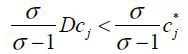 . Using unit costs in the North and the South (eq. 6), this condition corresponds
to
. Using unit costs in the North and the South (eq. 6), this condition corresponds
to
Firm produces when pa(j) < pb(j), which is
The exporting firm also produces for domestic good since condition in Eq. (9) is satisfied whenever condition in Eq. (8) holds. We define αj and αj as threshold values that make Eq. (8) and Eq. (9) hold in equality respectively.
III. Endogenous Technical Change
The previous section presented the basic environments in which goods are produced. The environments determine the demand for innovation. This section introduces production functions for innovation.
A. Direction of Technical Change
Research is done by hiring skilled labor only. Research can be directed toward improving on either zh or zl (or both). Profit is a function of zh, j and zl, j.
Innovator chooses zh,t+1 and zl,t+1. However, research costs increase with distance zh,t+1 − zh,t. Following the knowledge-based R&D specification from Acemoglu (2002), productivity in creating new technology is dependent on the current state of both s-augmenting and l-augmenting technology.
where 0 ≤ θ ≤ 1, 0 ≤ δ ≤ 1 and B ≤1. θ governs the returns to scale in technology production. δ is the degree of state dependence. When δ =1, each technology advancement depends only on their own state of technology and does not affect cost of developing the other. I allow the costs in innovating the two technologies to differ with parameter B. When B <1, it costs more to innovate on s-augmenting technology.
Empirical data finds a higher relative wage for the skilled to the unskilled in the North compared to the South. To incorporate this feature I use parameter ζ in s-augmenting technology where ζ ≥1. Parameter ζ is equal to 1 in the South. All analysis goes through when we set his parameter ζ equal to 1 in the North as well.
Entrant needs to pay fixed cost, fe, to initiate research. The fixed cost can be interpreted as wages paid to specialized labor which exists only for R&D, as in Aghion and Howitt (1992). Specialized labor has to be hired proportional to skilled labor hired in R&D.
Entry cost makes the ex-ante profit of the entrant equal to zero. The number of entrants is indeterminate but there is always one entrant who succeeds in innovation. Thus, the entrant is indifferent in which sector to innovate on. Entrant decides the employment level of the skilled labor in innovating each technology. The entrant reaps all profit as she becomes the monopolist selling the innovated good for the next period.
The entrant’s problem is
subject to innovation technology constraint, Eq. (10).
Optimal technology in the next period, zh,j,t+1 and zl,j,t+1, are solve from the first order conditions equations. 3 Then, the number of employees hired for innovation on s-augmenting and l-augmenting technology (hh,j,t and hl,j,t) is easily traced with innovation technology constraint of Eq. (10). There is a free entry condition equalizing profit and costs of innovation. I also assume that a constant fraction of profit is paid as wages to the skilled labor hired in research.4
IV. Equilibrium Analysis
This section defines the equilibrium of the model and provides an analysis of the balanced growth path. I focus on the effects of change in trade costs to study the implications for the skill premium in the North and the South when trade costs fall.
A. Equilibrium
Definition 1.
Equilibrium of the economy is composed of a sequence of aggregate prices 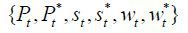 , aggregate quantity
, aggregate quantity 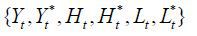 , sector prices for domestic good and export good
, sector prices for domestic good and export good 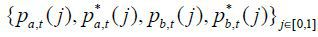 , sector quantities demanded and produced
, sector quantities demanded and produced 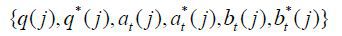 , firm’s profit, export decisions
, firm’s profit, export decisions 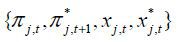 , factor demands for production
, factor demands for production 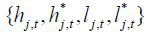 and for research
and for research 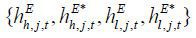 satisfying (intermediate and final good) producers’ and innovators’ optimality conditions,
while those equilibrium clear factors and goods markets and balance trade in the North
and the South.
satisfying (intermediate and final good) producers’ and innovators’ optimality conditions,
while those equilibrium clear factors and goods markets and balance trade in the North
and the South.
Using demand functions, firm profit can be expressed as
Profit is increasing as the unit cost is decreasing. Thus, profit increases when the technology advances.
Using Eq. (4) and (7), the quantities of domestic demand and foreign demand at equilibrium price are expressed as
Using Eq. (12), output produced in sector j is
Skilled labor and unskilled labor hired in production are, respectively,
From Eq. (13), the relative ratio of the skilled to the unskilled in sector j is
Skill premium is expressed as
Trade balance requires that all income is spent on the final non-traded good:
General equilibrium of this model is described as follows:
Given factor prices {s, s*, w, w*}, unit cost 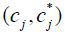 is derived from Eq. (6). Prices for intermediate goods are determined by a constant
markup over the unit costs from Eq. (5) and Eq. (7). Export decision is made based
on condition Eq. (8). Once the production decision is made from Eq. (9), unskilled
and skilled labor are hired following Eq. (13). In this step, we use normalized final
output. They produce αj,
is derived from Eq. (6). Prices for intermediate goods are determined by a constant
markup over the unit costs from Eq. (5) and Eq. (7). Export decision is made based
on condition Eq. (8). Once the production decision is made from Eq. (9), unskilled
and skilled labor are hired following Eq. (13). In this step, we use normalized final
output. They produce αj, 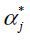 , bj,
, bj, 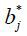 according to Eq. (12). From Eq. (3), aggregate price and quantity is retrieved using
the labor market clearing condition for unskilled labor, Eq. (C2). Profit is given
from Eq. (11). Next, Eq. (A1) and Eq. (A2) determines the number of researchers hired
in both s-augmenting and l-augmenting R&D for each sector. Equilibrium factor prices
should satisfy labor market clearing conditions and balance trade between the North
and the South.
according to Eq. (12). From Eq. (3), aggregate price and quantity is retrieved using
the labor market clearing condition for unskilled labor, Eq. (C2). Profit is given
from Eq. (11). Next, Eq. (A1) and Eq. (A2) determines the number of researchers hired
in both s-augmenting and l-augmenting R&D for each sector. Equilibrium factor prices
should satisfy labor market clearing conditions and balance trade between the North
and the South.
B. Balanced Growth Path
Definition 2.
Balanced growth path (BGP) is an equilibrium sequence where variables (research labor for each sector and each technology, skilled labor and unskilled labor for each sector) stay constant. Output and consumption grow at a constant rate. Skill premium and the threshold values αj, αj also stay constant.
Under complete specialization, where the North produces goods over αj and exports goods over αj, the aggregate equilibrium price is
In essence, what we solve in the general equilibrium are {s, s*, w, w*, Y, Y*} with labor market clearing conditions, Eq. (C1) and (C2) for each country, and the trade balance for the North and the South, Eq. (D2) and (D3).6
On the balanced growth path, sectors requiring more skilled labor, αj > αj, will export to country S. This corresponds to region C in Figure 1. And sectors requiring more unskilled labor, αj < αj imports from country S (region A). In the middle range sectors (region B), αj ∈ [αj, αj], goods will be produced and consumed within their country.
FIGURE 1.
SPECIALIZATION PATTERNS
Note: For country N, region A denotes sectors where goods are imported. Sectors in region B produce goods but the goods are consumed within country N. Region C sectors produce and they export to country S.
The difference in technology and relative factor endowments determine the pattern
of specialization. I show in the analysis below that range B will be broader when
trade cost, D, is higher or when the relative price of skilled labor to unskilled labor is not
significantly different in the two countries. Export is more likely when the relative
productivity 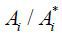 is high.
is high.
C. Analytical Results
The analytical results in this subsection rely on one parameter assumption as follows:
Assumption 1. Parameter values satisfy 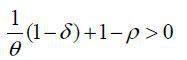
Parameters δ and θ governs R&D technology. ρ is the elasticity of substitution between skilled labor and unskilled labor. Estimated
value on ρ in the literature ranges from 1.2 to 1.4.7 The following results come under this assumption. When 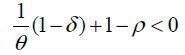 , then we cannot pin down relative technology in each sector since
, then we cannot pin down relative technology in each sector since 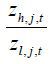 is a convex function of αj .
is a convex function of αj .
Propositions 1 and 2 indicate that the direction of technology change is different across countries. The proofs are in Appendix E.
Proposition 1. 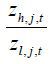 is increasing in αj and
is increasing in αj and 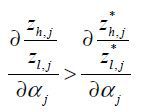 for ∀j. Moreover, when δ < 1,
for ∀j. Moreover, when δ < 1, 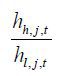 is increasing in αj.
is increasing in αj.
The first result shows that as the skill intensity of a sector increases, the ratio of innovation on s-augmenting technology to innovation on l-augmenting technology increases. The second result shows that the North directs more R&D towards skill-augmenting technology relative to labor-augmenting technology than the South in the sector with the same skill-intensity. Put differently, the South uses unskilled labor more efficiently than the North. The final result of Proposition 1 indicates that as skill intensity grows, more skilled labor is employed in the s-augmenting R&D sector to the l-augmenting R&D sector.
Proposition 2.  for ∀j ∈ [0,1].
for ∀j ∈ [0,1].
The proposition 2 shows that the (efficiency-adjusted) ratio of skilled labor in the s-augmenting R&D sector to the l-augmenting R&D sector is higher in the North than the South.
The following Proposition 3, 4, and 5 present analytical results on specialization and innovation when trade costs change.
Proposition 3. 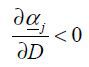 ,
, 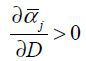 and
and 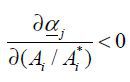 ,
, 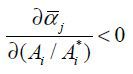 .
.
Threshold values for domestic production αj and for export αj are a function of trade costs and other parameters. The range of [αj, αj] shrinks as trade costs decrease. Thus, a larger variety of goods are traded when trade costs decrease. As the relative productivity of the North to the South increases, the ranges that the North produces and exports get wider.
Proposition 4. 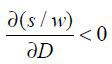 ,
, 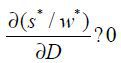 ,
, 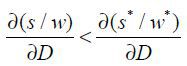
The skill premium in the North increases as trade costs decrease. When trade costs drop, the threshold value for domestic production, αj, increases. This allows the North to focus its resources in more skill-intensive sectors where they hire more skilled labor. Thus, the skill premium increases in the North. Moreover, a decrease in trade costs brings about a drop in the threshold value of domestic production for the South, αj. The South will put more resources in labor-intensive sectors. However, a change in the skill premium in the South can be positive or negative depending on the parameters and differences in general technology and endowments. Two forces are playing against one another in skill premium. On the one hand, production requires more unskilled labor, which will raise wages for the unskilled. On the other hand, demand for skilled labor increases to develop l-augmenting technology and that drives up wages for the skilled. Thus, the answer depends on the magnitude of each effect on the skill premium.
Proposition 5. Gains from trade are magnified due to endogenous directed technical change.
Gains from trade come from specialization based on the Heckscher-Ohlin effect. Trade allows countries to specialize in sectors that intensively use their relatively abundant factors. The gains are magnified by directed technical change. Thus, gains from trade are larger in this model compared to the case where there is no directed technical change or in the case where technical change is only allowed in the North. Endogenous technical change in the South lowers unit costs in the South. This lowers the price of intermediate goods as well as the aggregate price in both the North and the South. Real output increases due to directed technical change spurred by trade.
V. Concluding Remarks
This paper analyses how technology advancement is directed towards a particular factor of production in international trade between the North and the South. Cross-country differences in factor endowments and sectoral productivities affect incentives to invest in R&D toward each factor. The main result shows that more R&D is directed towards skill-augmenting technology in the North than in the South in the sector with the same skill-intensity. Trade allows the North to focus on more skill-intensive sectors not only in production but also in technology advancement. In both countries, technical change is more skill-biased as the skill intensity of sector increases.
As trade costs change, there is a reallocation of resources in both production and innovation. The North gets to produce and export more various goods that are most skill-intensive. The opposite happens with the South. These reallocations lead to a change in the skill premium. As trade costs decrease, skill premium in the North increases. A change of the skill premium in the South can be either positive or negative. The skill premium in the South can increase because the demand for skilled labor increases for R&D in technologies for labor-intensive products. My model can produce this result without relying on an assumption of a third country which is more skill-scarce. Moreover, the results are supported by the empirical findings that countries’ technologies make use of their relatively abundant endowment more efficiently.
Finally, there exist gains from trade not only due to specialization but also from endogenous directed technical change. Lowering trade costs allows countries to trade a larger variety of goods and to develop technologies in those added sectors. Thus, my model implies larger gains from trade compared to other models when the South only adopts technology developed by the North. Future interesting work can be undertaken by allowing endowments of skilled and unskilled labor to be endogenous.
Appendices
APPENDIX
A. F.O.Cs for Entrants
In section III, first order conditions of the entrants’ problem in innovation market are:
From the first order conditions, for each sector j, the following equality holds.
B. Free Entry Condition and Wages Paid to Research
Free entry condition equalizes profit obtained from innovation and the costs of innovation as follows:
Constant fraction φ of profit is paid to skilled labor hired in research. Thus,
D. Equilibrium Price and Trade Balance in the BGP
The aggregate price for the South satisfies
Trade balance in the North is
Trade balance in South is
E. Proofs
Proof of Proposition 1.
The share of expenditure on foreign goods is
On the balanced growth path, technology grows at a constant rate
Using Eq. (E1) on Eq. (A3), we have
Combining (E2) with Eq. (14), skill premium is
The first result of Proposition 1 is derived from equation Eq. (E2). When δ <1, equation Eq. (E1) proves the second result. ■
Proof of Proposition 2.
I prove Lemma 1 and 2 below first.
Lemma 1. 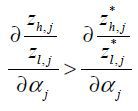 if and only if
if and only if 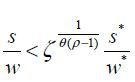 for ∀j,t.
for ∀j,t.
From Eq. (E2), we have
Comparing same equation for 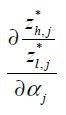 proves Lemma 1. ■
proves Lemma 1. ■
Lemma 2. In equilibrium, 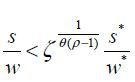 should be satisfied.
should be satisfied.
Suppose not. Then we have 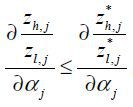 . This implies that
. This implies that 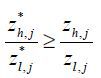 for all sectors. This is not compatible with the assumption that H / L ≥ H* / L*. There should exist some sectors in the North where they hire more skilled labor
to unskilled labor than in the South. ■
for all sectors. This is not compatible with the assumption that H / L ≥ H* / L*. There should exist some sectors in the North where they hire more skilled labor
to unskilled labor than in the South. ■
Using Lemma 2, 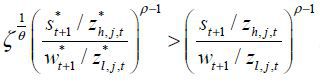 .
.
Skilled labor hired in each R&D is 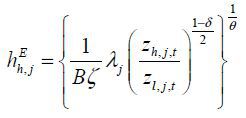 and
and 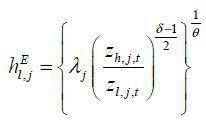 . Combining these equations with Lemma 1 proves Proposition 2. ■
. Combining these equations with Lemma 1 proves Proposition 2. ■
Notes
This paper is a revised version of the third chapter of Kim (2014). Special thanks to Ping Wang and the two anonymous referees. All errors are my own.
Zhu and Trefler (2005) show the evidence of rising inequality in the South using the Freeman and Oostendrop (2001) occupational wage database which covers 20 developing countries. See also Meschi and Vivarelli (2009) which use the UTIP-UNIDO database covering 65 developing countries.
The literature on the appropriate technology starts at least with Atkinson and Stiglitz (1969). Acemoglu and Zilibotti (2001) paper is more relevant to this paper since it focuses on differences in skill scarcity across countries.
References
. (2002). Directed Technical Change. The Review of Economic Studies, 69(4), 781-809, https://doi.org/10.1111/1467-937X.00226.
. (2003). Patterns of Skill Premia. The Review of Economic Studies, 70(2), 199-230, https://doi.org/10.1111/1467-937X.00242.
, & . (2001). Productivity Differences. The Quarterly Journal of Economics, 116(2), 563-606, https://doi.org/10.1162/00335530151144104.
, & . (1992). A Model of Growth through Creative Destruction. Econometrica, 60(2), 323-351, https://doi.org/10.2307/2951599.
, & . (2010). Innovation, Firm Dynamics, and International Trade. Journal of Political Economy, 118(3), 433-484, https://doi.org/10.1086/653690.
, & (1969). A New View of Technological Change. Economic Journal, 79(315), 573-578, https://doi.org/10.2307/2230384.
, & . (1997). Technological Diffusion, Convergence, and Growth. Journal of Economic Growth, 2(1), 1-26, https://doi.org/10.1023/A:1009746629269.
, & (1998). Appropriate Technology and Growth. Quarterly Journal of Economics, 113(4), 1025-1054, https://doi.org/10.1162/003355398555829.
, , & . (2016). Trade Induced Technical Change? The Impact of Chinese Imports on Innovation, IT and Productivity. The Review of Economic Studies, 83(1), 87-117, https://doi.org/10.1093/restud/rdv039.
, & . (2006). The World Technology Frontier. American Economic Review, 96(3), 499-522, https://doi.org/10.1257/aer.96.3.499.
, & (2001). The Occupational Wages Around the World Data File. International Labour Review, 140, 379-401, https://doi.org/10.1111/j.1564-913X.2001.tb00223.x.
, & (1992). Changes in Relative Wages, 1963-1987: Supply and Demand Factors. The Quarterly Journal of Economics, 107(1), 35-78, https://doi.org/10.2307/2118323.
, & (2009). Trade and Income Inequality in Developing Countries. World Development, 37(2), 287-302, https://doi.org/10.1016/j.worlddev.2008.06.002.
, & (1994). Barriers to Technology Adoption and Development. Journal of political Economy, 102(2), 298-321, https://doi.org/10.1086/261933.
. (2004). Factor Proportions and the Structure of Commodity Trade. American Economic Review,, 94(1), 67-97, https://doi.org/10.1257/000282804322970715.
, & . (2005). Trade and Inequality in Developing Countries: A General Equilibrium Analysis. Journal of International Economics, 65(1), 21-48, https://doi.org/10.1016/j.jinteco.2003.11.005.