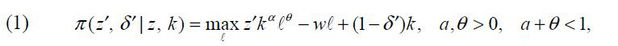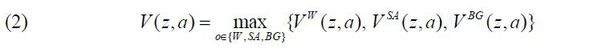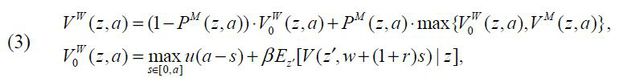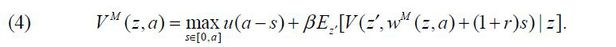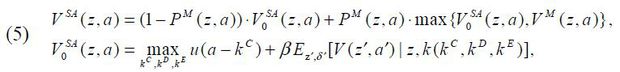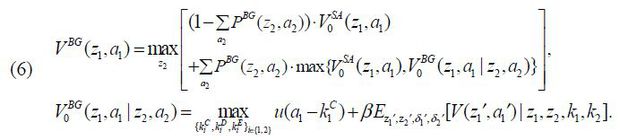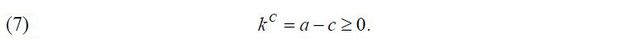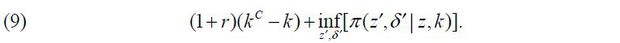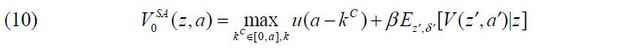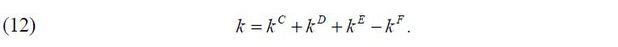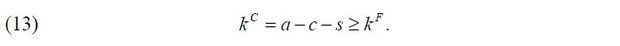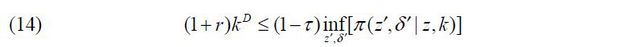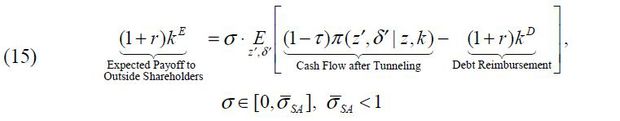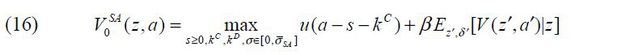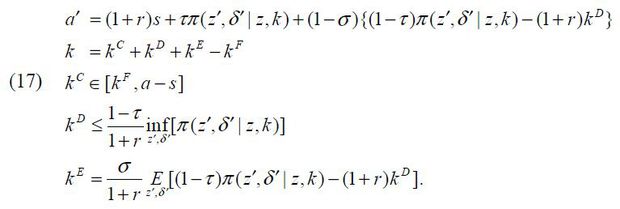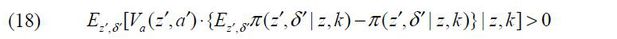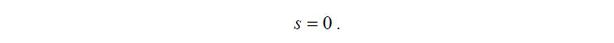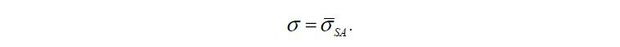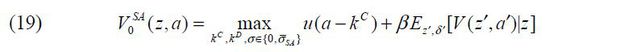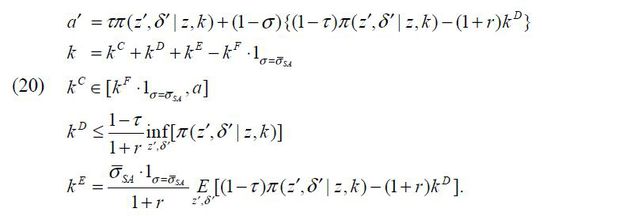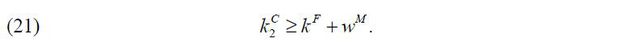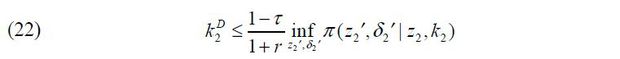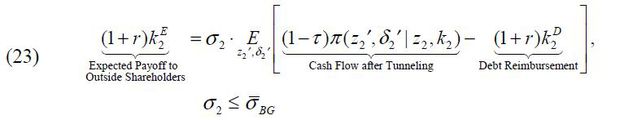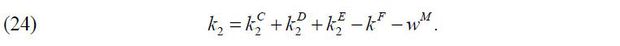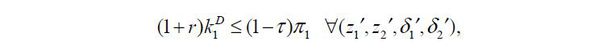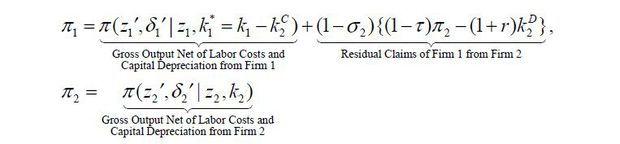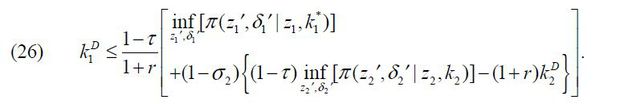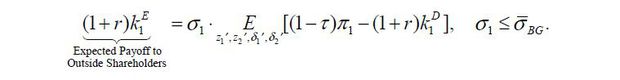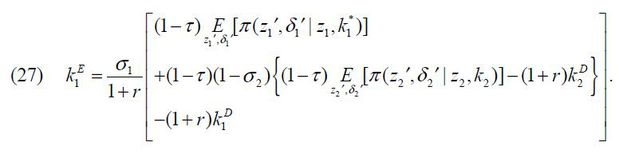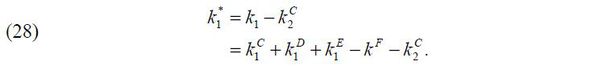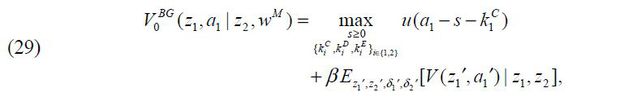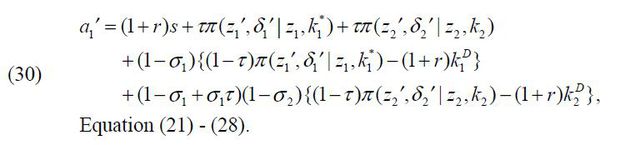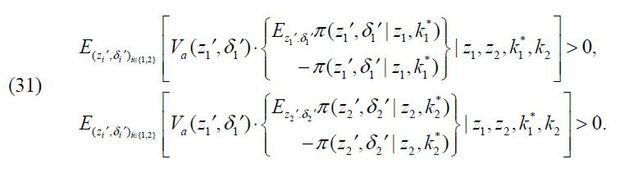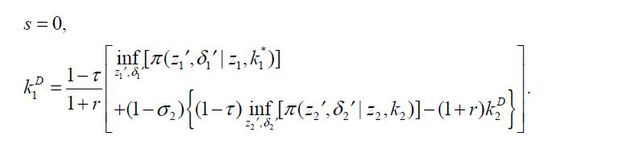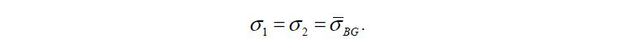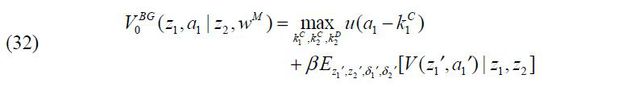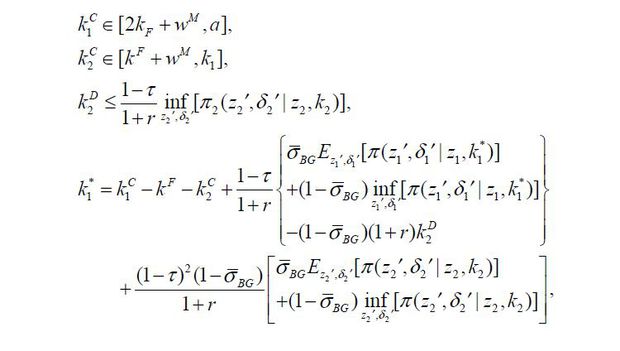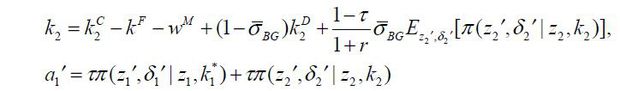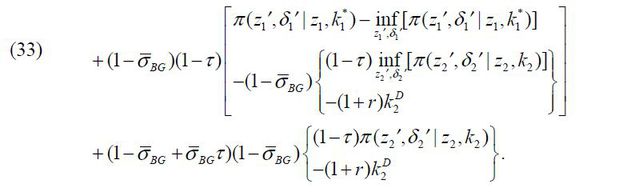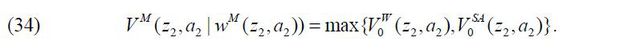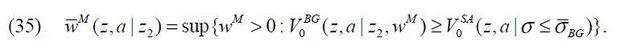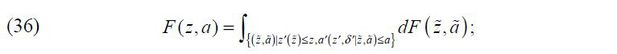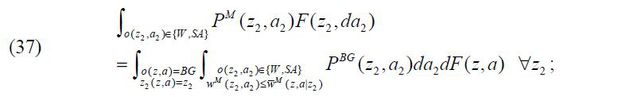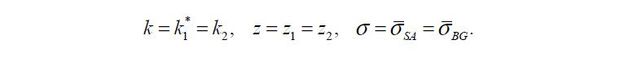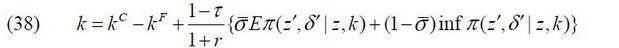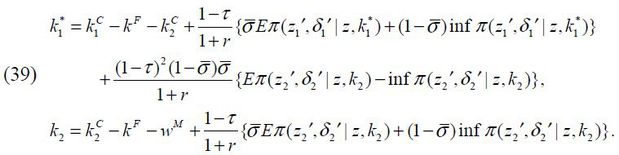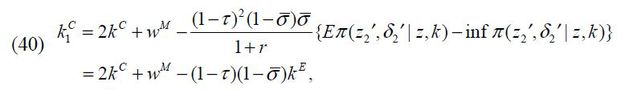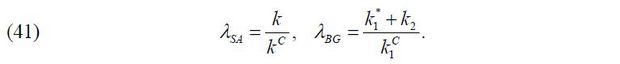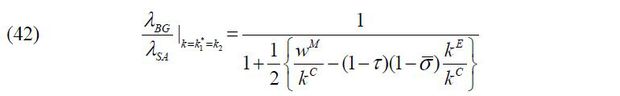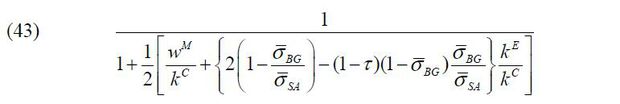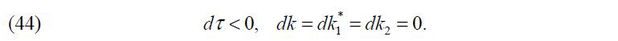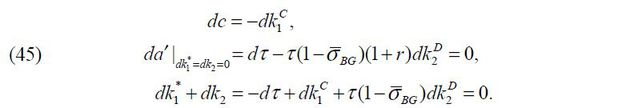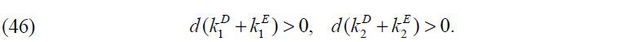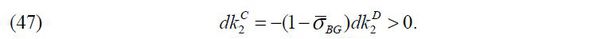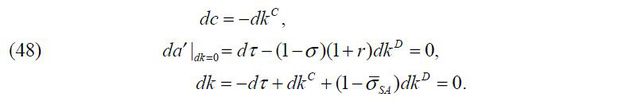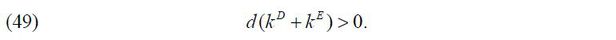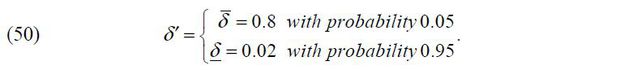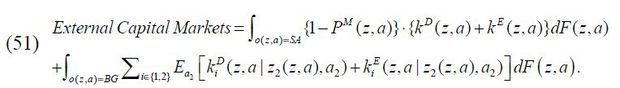Pyramidal Business Groups and Asymmetric Financial Frictions†
Abstract
Given capital market imperfections, an entrepreneur can alleviate financial frictions by creating a pyramidal business group in which a parent firm offers its subsidiary firm internal finance. This endogenous creation of pyramidal business groups can beget asymmetric financial frictions between business-group firms and stand-alone firms. I build a model to show that these asymmetric financial frictions can have sizable effects on resource allocation. On one hand, the financial advantage of pyramidal business groups can foster productive firms by incorporating them as subsidiaries. On the other hand, the asymmetrically large amount of external capital controlled by pyramidal business groups can be expended by unproductive business-group firms and push up the equilibrium price of capital. The model suggests that with fine investor protection or low financial frictions, the benefits of pyramidal business groups can be dominated by their costs because the probability of fostering productive subsidiaries diminishes as the efficiency of external capital markets improves, while the prevalence of pyramidal business groups is not attenuated due to their continuing asymmetric financial advantage.
Keywords
Business Group, Capital Market, Financial friction, Pyramidal Ownership Structure, Resource Allocation
JEL Code
E23, E44, G32, O16
I. Introduction
Apyramidal business group is a collection of legally independent corporations controlled by a coterie of shareholders. It is a common ownership structure for a country’s largest firms, with exceptions of some countries such as the United States or the United Kingdom.1 The economy-wide repercussions of pyramidal business groups, however, have been unclear despite the fact that they are salient economic institutions too sizable to be ignored. For instance, pyramidal business groups in South Korea not only have been acclaimed as engines of growth for the country’s rapid development but also have been the subjects of controversy for their economic concentration.2
In this paper, I build a model of pyramidal business groups in a general equilibrium framework and aim to answer the following question: Can pyramidal business groups affect the efficiency of an economy? I focus on a pyramidal ownership structure, which arises due to capital market imperfections and gives rise to asymmetric financial frictions between business-group firms and stand-alone firms.3
Built on the 'span of control' model developed by Lucas (1978), two assumptions are made here. First, I assume that capital markets are imperfect, constraining a firm’s ability to raise external capital. A limited commitment problem is introduced such that an entrepreneur controlling his or her firms can divert τ fraction of the firms’ cash flow before outside investors are reimbursed. In the model, this realized diversion keeps the expected rate of return on external equity finance identical to the risk-free interest rate. An entrepreneur, thus, can earn positive profits as the private benefits of control and has an incentive to create firms to control with flotation costs.4
Second, I allow for a business group as a private means that can alleviate financial frictions. In the model, a business group is constructed as a collection of two firms connected through a pyramidal ownership structure such that a business-group entrepreneur controls a parent firm that controls a subsidiary firm. There is no limited commitment problem between the parent and the subsidiary because both firms are controlled by the common entrepreneur. Thus, the parent can offer as much internal finance as possible to the subsidiary without financial frictions. Specifically, the financial advantage of a pyramidal business group in the model is twofold. Not only does the subsidiary use its internal equity finance offered by the parent as leverage to raise external capital, but also the parent uses its equity shares of the subsidiary as leverage to raise external capital. Thus, it is the financial advantage of a business group that makes it possible for an entrepreneur to build up a business group as a competitive ownership structure in equilibrium.
An occupational choice model is used to examine the impacts of business groups in a general equilibrium. I introduce an individual’s problem of occupational choices given heterogeneity in managerial talent and wealth throughout the population. Every period, each individual chooses his or her occupation from a worker, a stand-alone entrepreneur, a business-group entrepreneur, or a manager who can be hired by a business-group entrepreneur. Given the degree of financial frictions capturing capital market imperfections, three types of capital markets are specified: external debt, external equity, and internal equity markets. These three types of capital markets are used to build up three types of firms: a private company, a publicly held corporation, and a pyramidal business group. This variety of firms’ ownership structures captures private institutions stemming from agents’ endogenous reactions against capital market imperfections, which generates asymmetric financial frictions among the firms in the model.
The model shows that business groups can have a non-monotonic impact on resource allocation given the degree of financial frictions. In an economy with poor investor protection, the internal capital markets of business groups substitute for underdeveloped external capital markets and foster financially constrained but productive firms. A numerical example of the model shows that the rich become business-group entrepreneurs by hiring the poor but talented as business-group managers. It also shows that an economy with business groups accumulates a larger amount of capital stock than an economy without business groups because the rich save more in order to create business groups featuring internal capital markets. This implies that business groups can be efficient private institutions at the early stages of economic development, during which financial frictions are rampant.
In an economy with fine investor protection, however, the asymmetric financial frictions between business group firms and stand-alone firms become a source of resource misallocation. The rich but unproductive choose to create business groups despite flotation costs because they can earn ex-ante positive profits by incorporating productive subsidiaries, while their ex-post profits can be negative because the probability of launching productive subsidiaries declines with the rising managerial compensation as investor protection improves. Moreover, business-group entrepreneurs use their financial advantage to consume more and save less by raising a larger amount of external capital without increasing net capital in production. Thus, the larger demand and the lower supply of capital push up the equilibrium price of capital and force stand-alone entrepreneurs, most of whom are financially constrained, to raise less external capital, produce less, and consume less. This numerical example shows that stand-alone entrepreneurs’ wealth drops significantly and that an economy dominated by business groups features decreasing levels of capital stock and stagnating aggregate consumption as the fraction of diversion τ goes to zero.
An interesting lesson we can learn from the model is that the relative number of business-group firms in the numerical example does not decrease endogenously with the improvement of investor protection. This occurs because the incentive for an entrepreneur to build a business group in the model is not attenuated unless the asymmetric financial frictions between the business group and the stand-alone firms shrink. This result is consistent with Masulis, Pham, and Zein (2011), who report an insignificant association between the prevalence of family business groups and the degree of investor protection. Given that the direction of effects business groups have on an economy in the model is reversed as investor protection improves, the unvarying number of business-group firms implies that mitigating capital market imperfections will scarcely reduce factor misallocation or even worsen it without due consideration of pyramidal business groups, which could generate asymmetric financial frictions in equilibrium.
Although I simplify the problem of business groups by focusing on the financial advantage of their internal capital markets, there is a larger pool of questions about business groups that should be examined, such as questions pertaining to monopolies, political economies, risk sharing, or the intangible assets of business groups. For example, Khanna and Yafeh (2007) review several issues of business groups and conclude that their origins and effects are largely unknown. Note that the objective of this paper is to narrow down the problem and understand a certain trait of business groups, their internal capital markets, in a general equilibrium framework.
In the literature, the pyramidal ownership structure of a business group has been examined from two different viewpoints. First, a traditional view is that it is an expropriation device. The main argument of this view is that the pyramidal ownership structure creates a discrepancy between ownership and control. Although the controlling shareholder of a business group, typically a family, owns a small portion of the shares of business-group affiliates, its pyramidal scheme allows the family to take control over the business group and to earn the private benefits of control at the expense of other shareholders. This separation of ownership from control can generate agency problems, resource misallocation, and economic entrenchment. See Morck, Wolfenzon, and Yeung (2005) for a review of this perspective.
Second, more recent studies examine pyramidal business groups as start-up breeders. They focus on the role of business groups that offer internal finance to start-up firms and help them grow larger by supplementing the inefficiency of external capital markets. Almeida and Wolfenzon (2006b) offer a theory of business groups based on the financial advantage of pyramidal business groups. In their model, the controlling shareholder of a parent firm uses the firm’s retained earnings to launch a subsidiary firm that provides cash flow to the controlling shareholder. Despite the discrepancy between ownership and control, business groups can be economically beneficial because subsidiary firms would be dismissed without the help of internal capital markets due to setup costs that cannot be raised from external capital markets given financial frictions. Bena and Ortiz-Molina (2013) use data from 38 European countries and show that business groups do play a significant role in creating new firms.
These two perspectives on pyramidal business groups are not mutually exclusive. They are rather opposite sides of the same coin in that the first can cause the second. The opportunity to earn additional cash flow from a subsidiary firm is an incentive for the controlling shareholder of a parent firm, which offers internal finance and helps to launch its subsidiary firm.
A natural question arises. Between these two viewpoints, which aspect of business groups is dominant? Simply put, are business groups good or bad for an economy? In spite of its relevance, the answer to this question has remained unclear, as most researchers have focused on the internal efficiency of an individual business group. Few researchers have developed models of business groups in a general equilibrium framework.
Among them, Almeida and Wolfenzon (2006a) show that the financial advantage of business groups can cause asymmetric financial frictions between business-group firms and stand-alone firms, which result in factor misallocation in equilibrium. Despite its novel insight, their model is stylized, making it difficult when using it to capture the dynamic aspects of an economy allowing for forward-looking behaviors of individuals, such as savings or self-financing. This can be a problem if we want to examine the economic impact of asymmetric financial frictions because the wealth distribution of an economy is endogenously determined by the agents’ dynamic optimization, which may undo factor misallocation stemming from financial frictions (e.g., Moll, 2014).
Ševčík (2015) examines the economic impact of business groups using a heterogeneous agent model with financial frictions in which the wealth distribution of an economy is endogenously determined. He studies the extent to which the internal capital markets of business groups can alleviate financial frictions and concludes that aggregate output in Canada would be reduced by 3% if its business groups were shut down. The business groups in his model, however, are partnerships rather than pyramids. This can be a problem if we want to examine the economic repercussions of pyramidal business groups that feature the separation of ownership from control. Specifically, in his model the degree of financial frictions captured by the ratio of capital to wealth is a given constant identical for all firms, while in the present model the ratio is endogenously determined and business-group entrepreneurs leverage their wealth into control over capital worth vastly more through a pyramidal ownership structure.
In order to deal with these limitations, I introduce the following feature in my model. First, each individual chooses his or her consumption, savings, and occupation every period. Thus, the joint distribution of individuals’ wealth and occupations is endogenously determined. Second, an individual who chooses to be an entrepreneur also chooses his or her firms’ ownership structure. I connect corporate capital structures with corporate ownership structures given capital market imperfections. A pyramidal business group is introduced as a private means by which an entrepreneur alleviates financial frictions. Thus, asymmetric financial frictions among firms arise from the endogenous choice of the firms’ ownership structures.
The rest of this paper proceeds as follows. In Section 2, I introduce an individual’s problem of occupational choice. In Section 3, given financial frictions, three types of capital markets and three types of firms are specified. In Section 4, a stationary equilibrium is defined by introducing a matching rule between a business-group entrepreneur and a manager. In Section 5, I remark on the model. The costs and benefits of pyramidal business groups are discussed. In Section 6, a numerical example of the model is constructed and the results of the model are presented. Lastly in Section 7, I discuss the limitations of the model and propose future research directions.
II. A Heterogeneous Agent Model with Occupational Choices
A. Economic Environment
An economy consists of infinitely lived individuals. Every period, each individual
is endowed with an indivisible labor force and characterized by his or her own managerial
talent z that changes over periods following a Markov chain.5 Here, we assume that an individual consumes c out of his or her own wealth a such that c∈[0, a] and that a utility function u(c) satisfies standard conditions such that u′(c) > 0, u′′(c) < 0, and 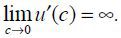
Given (z,a) , an individual chooses his or her next period occupation o(z,a) from a worker (W) , a stand-alone entrepreneur (SA) , or a business-group entrepreneur (BG) . At the beginning of the next period, a worker sells his or her indivisible labor force and earns wage w, and an entrepreneur runs a firm and earns from the firm’s stochastic cash flow π .
An entrepreneur raises her firm’s capital k given (z,a) . At the beginning of the next period, the entrepreneur observes a shock to the managerial talent z′ and hires labor l given k .6 The firm then produces cash flow π , defined as the optimized gross output net of labor costs wl and capital depreciation δ′k, such that
where a +θ < 1 is a span of control shaping the production function into decreasing returns to scale. We assume that the capital depreciation rate δ′∈(0, 1) is a random variable independent of z′ .
A stand-alone entrepreneur can run either a private company or a publicly held corporation. A private company is a firm fully owned by its stand-alone entrepreneur, and it raises capital from external debt markets. A publicly held corporation can be incorporated by its stand-alone entrepreneur who pays flotation costs kF . It can raise capital from external equity markets as well as external debt markets.
A business group is defined as a collection of two corporations: a parent that offers internal equity finance and a subsidiary that receives internal equity finance. An individual of (z1, a1) , 7 who chooses to be a business-group entrepreneur o(z1, a1) = BG, runs the parents with z1 and hires a manager of (z2, a2) who runs the subsidiary with z2 . The business-group entrepreneur can choose z2 , while a2 is randomly drawn with a probability of PBG (z2, a2) . The business-group entrepreneur earns from the cash flow of both firms at the beginning of the next period.
An individual of (z,a) , who chooses to be a worker or a stand-alone entrepreneur o(z, a)∈{W, SA}, can be matched to a business-group entrepreneur with a probability of PM (z, a). If the matching is realized, the individual becomes a manager and earns managerial compensation wM (z,a) at the beginning of the next period. Note that the managerial compensation wM is a function of (z,a) , which is pinned down when the matching is realized despite the fact that the subsidiary firm’s production will be realized with z′ in the next period.
Figure 1 summarizes the timing of an individual’s problem within a period. Given (z,a) , an individual initially chooses his or her occupation, after which the matching between business-group entrepreneurs and the others are realized. Finally, the output is produced with realized shocks to managerial talent z′ at the beginning of the next period.
B. An Individual’s Problem
Every period, each individual solves the following problem given his or her managerial talent z and wealth a such that
given {r,w,wM (z,a),PM (z,a),PBG (z2,a2)}, which respectively stand for the rate of return on capital, the wage for a worker, managerial compensation, the probability of being matched with a business-group entrepreneur, and the probability of being matched with a manager featuring (z2,a2) .
VW (z,a) is the value if an individual chooses to be a worker such that
where s is the risk-free asset matured in the next period with interest rate r .
VM (z,a) is the value if an individual becomes a manager given wM (z,a) such that
Note that both the next-period wealth for a worker, w+ (1+r)s, and that for a manager, wM (z,a) + (1+r)s, are realized without uncertainty.
VSA (z,a) is the value if an individual chooses to be a stand-alone entrepreneur who runs a private company or a publicly held corporation such that
where the firms’ capital in production k is a function of private finance kC, external debt finance kD, and external equity finance kE. The entrepreneur’s next-period wealth a′ is a function of shocks to managerial talent z′ and the capital depreciation rate δ′ given {kC, kD, kE}.
Lastly, VBG(z1 ,a1) is the value if an individual of (z1 ,a1) chooses to be a business-group entrepreneur who controls a business group consisting
of two corporations, a parent with (z1 ,k1) and a subsidiary with (z2 ,k2) . The business-group entrepreneur determines both firms’ capital amounts k1 and k2 by choosing 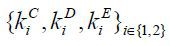 given {z2, wM (z2 ,a2)}.
given {z2, wM (z2 ,a2)}. 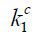 is the private finance that the business-group entrepreneur offers to the parent,
and
is the private finance that the business-group entrepreneur offers to the parent,
and 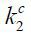 is the internal equity finance that the parent offers to the subsidiary. I will specify
how the business-group entrepreneur optimizes k1 and k2 in the following section. For now, the focus is on how the business-group entrepreneur
chooses z2, the optimal managerial talent for the subsidiary, given wM (z2 ,a2) and PBG (z2 ,a2) such that
is the internal equity finance that the parent offers to the subsidiary. I will specify
how the business-group entrepreneur optimizes k1 and k2 in the following section. For now, the focus is on how the business-group entrepreneur
chooses z2, the optimal managerial talent for the subsidiary, given wM (z2 ,a2) and PBG (z2 ,a2) such that
The business-group entrepreneur’s next-period wealth a1′ is a function of (z1′,δ1′, z2′,δ2′) given the firms’ capital structure 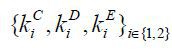 . Note that the probability of matching with a manager PBG (z2, a2) is endogenously determined in a stationary equilibrium and that its sum can be less
than one such that
. Note that the probability of matching with a manager PBG (z2, a2) is endogenously determined in a stationary equilibrium and that its sum can be less
than one such that 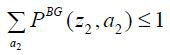 . If the demand of z2 is higher than the supply of z2, some business-group entrepreneurs would fail to be matched with their targeted managers
featuring z2.
. If the demand of z2 is higher than the supply of z2, some business-group entrepreneurs would fail to be matched with their targeted managers
featuring z2.
Figure 2 is an expository diagram of an individual’s occupational choice given his or her managerial talent z and wealth a.8 First, it shows that the poor and untalented are likely to become workers because they are not productive enough to run firms and because they do not have enough wealth to hire managers. Secondly, it shows that the more talented one is, the more likely they are to become entrepreneurs. A declining line separating SA from W captures financial frictions with which would-be entrepreneurs could become workers if they do not have enough wealth. Lastly, it shows that the rich tend to become business-group entrepreneurs because they can pay managerial compensation and hire talented individuals as business-group managers running subsidiary firms.
III. Financial Frictions and Three Types of Firms
Suppose that an entrepreneur who controls her firm can divert τ fraction of the firm’s cash flow. The tunneling ratio τ captures the degree of financial frictions in an economy. Accordingly, (1−τ) captures the degree of investor protection in an economy because (1−τ) is the residual cash flow investors can enforce on a firm if the firm does not undertake reimbursements.9
Given financial frictions, an entrepreneur can choose her firms’ ownership structure: a private company, a publicly held corporation, or a pyramidal business group. Specifically, an entrepreneur can run her private company, which is only allowed to access external debt markets with the help of the entrepreneur’s wealth as collateral. I assume that the external debt finance is bounded above by the firm’s lowest cash flow in order to guarantee its repayment.
To raise more external finance, an entrepreneur can pay flotation costs and incorporate a publicly held corporation that can tap into external equity markets. I assume that an entrepreneur owns all shares of her firm at the onset of its incorporation, which can be sold to outside shareholders to raise external equity finance. The extent of external equity finance her firm can raise is assumed to be proportional to the firm’s expected cash flow and the fraction of shares sold to outside shareholders.
Lastly, an entrepreneur can hire a manager with managerial compensation and build up a business group that consists of two corporations, a parent run by the entrepreneur and a subsidiary run by the manager. The business-group entrepreneur uses a pyramidal ownership structure to control both firms and makes the parent offer internal equity finance to the subsidiary without financial frictions. Similar to stand-alone corporations, both the parent and the subsidiary can sell their shares to outside shareholders and raise external equity finance.
A. A Private Company
Given her managerial talent and wealth, (z,a) , an entrepreneur can run a private company that is a firm fully owned by her. Due to the lack of external equity finance, a private company relies on external debt finance. The firm’s capital in production k is determined as follows. First, the entrepreneur of a private company is obliged for the company’s liability so that her wealth net of consumption a − c becomes the firm’s collateral kC such that
Second, given the collateral kC and the opportunity of diversion τπ, the firm’s capital in production k is bounded above as follows.
Lastly, the entrepreneur of a private company can choose k and decide how much external debt finance will be raised. I assume that the firm, or the entrepreneur, can invest in a risk-free asset by taking k < kC. Thus, the entrepreneur can earn a risk-free residual cash flow from the firm such that
To summarize, a stand-alone entrepreneur running a private company solves
subject to
The entrepreneur of a private company can divert her firm’s cash flow. The total cash flow she earns, however, is the sum of the diverted cash flow and the residual cash flow after debt repayment, which is identical to the non-diverted cash flow after debt repayment. Unlike the publicly held corporations or business groups introduced in the following sections, we can therefore interpret that in equilibrium, diversion does not occur in a private company that is fully owned by its entrepreneur.
B. A Publicly Held Corporation
An entrepreneur of (z,a) can choose to incorporate her firm into a publicly held corporation with flotation costs kF > 0. After its incorporation, a publicly held corporation can tap into external equity markets. The corporation’s capital in production k is determined by the sum of private finance kC, external debt finance kD, and external equity finance kE, net of flotation costs kF such that
Each type of capital is determined as follows. First, the entrepreneur can transfer a fraction of her wealth kC to her corporation. kC is determined by the entrepreneur’s wealth a net of her consumption c and private risk-free asset s. I assume that the flotation costs kF should be paid by the entrepreneur with kC before the firm’s incorporation such that10
In contrast to a private company, the entrepreneur’s wealth cannot be used as collateral for her corporation because a publicly held corporation is a legal entity that is separate from its entrepreneur. According to this construction, however, the wealth transfers from its entrepreneur to the publicly held corporation work as collateral; this is why I abuse the notation of kC.
Second, a publicly held corporation can use external debt finance kD. Given the assumption that an entrepreneur controlling her firm can divert τ fraction of the firm’s cash flow π , the external debt finance kD is constrained in order to guarantee its repayment, as follows. Note that a publicly held corporation can invest in a risk-free asset by taking kD < 0.
Third, a publicly held corporation can tap into external equity markets. The corporation can raise external equity kE = kE (σ) by selling its σ ∈ [0, σSA] fraction of shares. Suppose that (1 − σSA) > 0 fraction of the firm’s shares is required for an entrepreneur to take control of his or her stand-alone corporation. I assume that external capital markets are competitive and well diversified so that the publicly held corporation can raise external equity with the risk-free interest rate r.
As can be observed in the above equation, the firm’s cash flow π is sequentially distributed to the entrepreneur with tunneling τπ , to creditors with debt reimbursement (1+ r)kD , and to shareholders with residual claims.
To summarize, a stand-alone entrepreneur running a publicly held corporation solves
subject to
Condition 1. The Value function V(z,a) satisfies the following condition:
Condition 1 describes an entrepreneur running a firm who is averse to risk. Note that
if the marginal value of wealth Va monotonically decreases in wealth a, Condition 1 holds. Va, however, is not in general a monotonically decreasing function of a. The individual’s value function V(z,a) may be locally convex even when its underlying utility function is concave because
the individual’s choice set is non-convex. We need an additional structure to hold
Condition 1. Henceforth, we assume that for all (z, k), a minimum cash flow 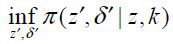 is low enough to satisfy Condition 1. Given that the marginal utility of consumption
goes to infinity as consumption goes to zero, the marginal value of wealth Va(z′,a′) with the sufficiently low minimum cash flow can be large enough to make the left-hand
side of equation (18) positive.
is low enough to satisfy Condition 1. Given that the marginal utility of consumption
goes to infinity as consumption goes to zero, the marginal value of wealth Va(z′,a′) with the sufficiently low minimum cash flow can be large enough to make the left-hand
side of equation (18) positive.
Proposition 1. Given the risk-free investment opportunity for a corporation, kD < 0, a standalone entrepreneur weakly prefers not to hold private assets such that
Given Condition 1 and the risk-free investment opportunity, a stand-alone entrepreneur of a publicly held corporation strictly prefers fully external equity finance such that
Proof. See Online Appendix B.11
Corollary 1. From Proposition 1, the stand-alone entrepreneur’s choice variables degenerate into {kC, kD,σ}. Thus, we can simplify the problem of a private company and that of a publicly held corporation into the common problem of a stand-alone entrepreneur such that
subject to
C. A Business Group
A business group is defined as a collection of two publicly held corporations, Firm 1 and Firm 2, which are controlled by a business-group entrepreneur. Let z1 denote the productivity of Firm 1 that inherits from the business-group entrepreneur and let z2 be the productivity of Firm 2 that inherits from the manager.
We assume that a business group is connected through a pyramidal ownership structure
such that Firm 2 is owned and controlled by Firm 1 that is owned and controlled by
a business-group entrepreneur. More specifically, the business-group entrepreneur
incorporates Firm 1 with private finance 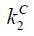 , keeps at least (1−σBG) shares of Firm 2, and controls Firm 2. I assume that the manager of Firm 2 takes
managerial compensation wM (z2,a2) relinquishes her control rights and cash flow rights over Firm 2, and hands them
over to Firm 1. As a result, the entrepreneur of a business group can control both
firms and divert cash flow from both firms.
, keeps at least (1−σBG) shares of Firm 2, and controls Firm 2. I assume that the manager of Firm 2 takes
managerial compensation wM (z2,a2) relinquishes her control rights and cash flow rights over Firm 2, and hands them
over to Firm 1. As a result, the entrepreneur of a business group can control both
firms and divert cash flow from both firms.
Two items here are important to note. First, the pair of managerial talent z2 and its corresponding managerial compensation wM (z2,a2) can be understood as a contract between an entrepreneur buying z2 and a manager selling z2 with the price of wM (z2,a2). Thus, the manner in which wM (z2,a2) is pinned down can be critical in the model. Given the lack of managerial talent markets, I assume that wM (z2,a2) is a certainty equivalent for an individual, who can run a stand-alone firm or become a worker as outside options. This will be formally specified in the following section.
Second, I assume that (1−σBG) fraction of shares is required to acquire control rights over a business group. σBG can differ from that of a stand-alone firm, σSA, because (1−σBG) needs to capture large enough block shares in order to ensure exclusive control rights over business-group firms, while (1−σSA) only captures the stand-alone entrepreneur’s payoff structure proportional to the firm’s cash flow. Thus, I assume that σBG ≤ σSA, although the model lacks a micro-foundation with regard to pinning down σSA and σBG.
1. Capital Structure of Firm 2
For now, suppose that Firm 2 is run by a manager who has z2 and a2. I assume that the flotation costs kF and the managerial compensation wM = wM (z2, a2) should be paid by Firm 1 through internal equity finance 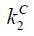 such that
such that
This implies that Firm 2 should be incorporated before tapping into external capital
markets. Firm 2 raises external debt finance 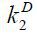 under the following constraint given the assumption that the business-group entrepreneur,
who controls Firm 1 that controls Firm 2, can expropriate cash flow from Firm 2.
under the following constraint given the assumption that the business-group entrepreneur,
who controls Firm 1 that controls Firm 2, can expropriate cash flow from Firm 2.
Firm 2 raises external equity finance 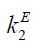 by selling its σ2 fraction of shares.
by selling its σ2 fraction of shares.
From the equations above, the capital in production of Firm 2, k2 , is determined by the sum of internal equity finance 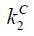 , external debt finance
, external debt finance 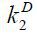 , and external equity finance
, and external equity finance 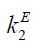 net of flotation costs kF and managerial compensation wM such that
net of flotation costs kF and managerial compensation wM such that
2. Capital Structure of Firm 1
A business-group entrepreneur of (z1,a1) can transfer her wealth 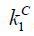 to Firm 1. I assume that both firms’ flotation costs and Firm 2’s managerial compensation
should be paid by the entrepreneur with
to Firm 1. I assume that both firms’ flotation costs and Firm 2’s managerial compensation
should be paid by the entrepreneur with 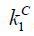 such that
such that
This arises not only because the timing of incorporating both Firm 1 and Firm 2 is simultaneous in the model but also because the contract between the entrepreneur and the manager should be established before Firm 2 is incorporated.
Given the capital structure of Firm 2, 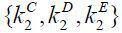 , and its cash flow, π(z2′, δ2′ | z2, k2), Firm 1 raises external debt finance
, and its cash flow, π(z2′, δ2′ | z2, k2), Firm 1 raises external debt finance 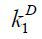 under the following constraint,
under the following constraint,
where π1 is the gross cash flow from Firm 1, defined as
We can rewrite the above inequality such that
Conceptually, the internal equity finance 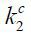 used by Firm 2 should be raised from Firm 1’s retained earnings (e.g., Almeida and Wolfenzon, 2006b). Given the limitation that firms are created and liquidated every period, however,
I use Firm 1’s capital k1 as a proxy for Firm 1’s retained earnings. Thus, the internal equity finance
used by Firm 2 should be raised from Firm 1’s retained earnings (e.g., Almeida and Wolfenzon, 2006b). Given the limitation that firms are created and liquidated every period, however,
I use Firm 1’s capital k1 as a proxy for Firm 1’s retained earnings. Thus, the internal equity finance 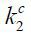 is raised out of k1, and Firm 1’s capital in production becomes
is raised out of k1, and Firm 1’s capital in production becomes 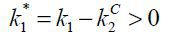 .
.
Lastly, Firm 1 raises external equity finance 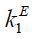 by selling its σ1 fraction of shares to outside shareholders such that
by selling its σ1 fraction of shares to outside shareholders such that
This equation can be rewritten as follows.
From the equations above, the capital in production of Firm 1, 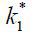 , is determined by the sum of private finance
, is determined by the sum of private finance 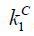 , external debt finance
, external debt finance 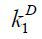 , and external equity finance
, and external equity finance 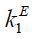 , net of flotation costs kF and internal equity finance
, net of flotation costs kF and internal equity finance 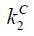 such that
such that
3. A Business-Group Entrepreneur’s Problem
Given (z2,a2) and wM = wM (z2,a2), a business-group entrepreneur of (z1,a1) solves the following problem,
subject to
Condition 2. The value function V(z1,a1) satisfies the following conditions:
Proposition 2. Given non-negative financial frictions τ > 0 and the risk-free investment opportunity of Firm 2 such that 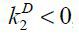 , a business-group entrepreneur weakly prefers no private risk-free asset and a full
external debt finance of Firm 1 such that
, a business-group entrepreneur weakly prefers no private risk-free asset and a full
external debt finance of Firm 1 such that
Given Condition 2 and the risk-free investment opportunity of Firm 2, a business-group entrepreneur strictly prefers full external equity finance of both firms such that
Proof. See Online Appendix C.
Corollary 2. From Proposition 2, the business-group entrepreneur’s choice variables degenerate
into 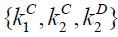 . Thus, we can rewrite the business-group entrepreneur’s problem as follows.
. Thus, we can rewrite the business-group entrepreneur’s problem as follows.
subject to
Note that in Corollary 2, Firm 1’s capital in production 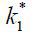 decreases with
decreases with 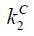 but increases with the cash flow of Firm 2, π(z2′, δ2′ | z2,k2) on the right-hand side of
but increases with the cash flow of Firm 2, π(z2′, δ2′ | z2,k2) on the right-hand side of 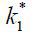 . Given that π(z2′, δ2′ | z2,k2) increases with k2 and that k2 increases with
. Given that π(z2′, δ2′ | z2,k2) increases with k2 and that k2 increases with 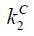 , we find that the financial advantage of a business group derives not only from no
limited commitment problems such that
, we find that the financial advantage of a business group derives not only from no
limited commitment problems such that 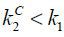 but also from an increase in the cash flow from Firm 2 to Firm 1.
but also from an increase in the cash flow from Firm 2 to Firm 1.
IV. A Matching Rule and a Stationary Equilibrium
A. A Matching Rule between Business-Group Entrepreneurs and Others
To complete the model, we consider an ad-hoc matching rule. It is designed to mitigate the gap between the model and the real world. Although the model assumes one-period matching between a business-group entrepreneur and a manager by construction, in the real world the matching between a business-group entrepreneur of (z,a) and a subsidiary Firm 2 of z2 is stable over time.
First, we assume that managerial compensation wM (z2,a2) is equal to the certainty equivalent for a manager who has outside options such that
This assumption implies that a business-group entrepreneur acquires all of the gains from building a business group and that the manager of Firm 2 will have less wealth in the next period than the expected wealth a stand-alone entrepreneur would have due to the risk-averse preference.
Second, we assume that the business-group entrepreneur can choose z2 but cannot choose a2. A business-group entrepreneur and its manager of Firm 2 who has a2 are randomly matched given z2. As a result, while an individual always accepts the offer of being a manger given the managerial compensation as a certainty equivalent, a business-group entrepreneur of (z,a) can turn down the opportunity of launching a subsidiary Firm 2 if the matched manager has too high a2 that induces wM(z2,a2) > wM (z,a|z2), where wM (z,a|z2) is the largest managerial compensation a business-group entrepreneur of (z,a) can be better off such that
Lastly, assume that a business-group entrepreneur, who screens out wM(z2,a2) > wM (z,a|z2) and gives up the opportunity of launching a subsidiary Firm 2, should keep at least (1−σBG) shares of Firm 1. This assumption begets a business group without Firm 2, which sells only σBG fraction of shares, not σSA. Although the capital structures of a business group without Firm 2 is ex-post suboptimal, it is ex-ante optimal for a business-group entrepreneur who wants to launch Firm 2 with the possibility of being matched with wM(z2,a2) ≤ wM (z,a|z2). The possibility of no subsidiary Firm 2 can be understood as an opportunity cost for a business-group entrepreneur. Given the limitation of the model defining a business group as a collection of two corporations, a business group without Firm 2 can be understood as a business group with fewer pyramidal layers.
B. A Stationary Equilibrium
Given the matching rule, a stationary equilibrium consists of a stationary joint distribution
of managerial talent and wealth F(z,a); the probability of being hired as a manager PM (z,a) and the probability of being matched with a manager PBG (z2,a2); prices {r,w,wM (z2,a2)}; and individual policy functions such as (i) occupation o(z,a) for an individual, (ii) the private risk-free asset s(z,a) for a worker or a manager, (iii) private finance kC (z,a), external debt finance kD(z,a), and external equity finance kE(z,a) for a stand-alone entrepreneur, (iv) the optimal managerial talent for a subsidiary
firm z2(z,a), private finance 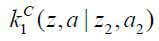 , internal equity finance
, internal equity finance 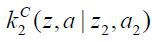 , and external debt finance
, and external debt finance 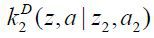 for a business-group entrepreneur matched with wM (z2,a2) ≤ wM (z,a|z2), and (v) private finance kC (z,a) and external finance kD (z,a) for a business-group entrepreneur matched with wM (z2,a2) ≤ wM (z,a|z2) such that
for a business-group entrepreneur matched with wM (z2,a2) ≤ wM (z,a|z2), and (v) private finance kC (z,a) and external finance kD (z,a) for a business-group entrepreneur matched with wM (z2,a2) ≤ wM (z,a|z2) such that
1. Given the stationary joint distribution of managerial talent and wealth F(z,a), the probability of being hired as a manager PM (z,a), the probability of being matched with a manager PBG (z2,a2), and prices {r,w,wM (z2,a2)}, the individual policy functions solve the individual’s problem in Section 2.2;
2. The joint distribution of managerial talent and wealth F(z,a) is stationary such that
3. The probability of a worker or a stand-alone entrepreneur being hired as a manager, PM (z2,a2), and the probability of a business-group entrepreneur being matched with a manager, PBG (z2,a2), satisfy the following condition:
4. Capital market and labor market clear. See Online Appendix A for a full description.
V. Remarks on the Model
A. Financial Advantage of Business Groups
In order to gauge how well internal capital markets can alleviate exogenous financial frictions in the model, we consider how much private wealth of an entrepreneur is required to raise a fixed amount of capital in production given the ownership structure of firms.
Suppose that a business group consists of two firms that replicate a stand-alone firm’s capital structure with identical managerial talent such that
We now compare the required level of private finance for a stand-alone firm kC to that for a business group 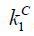 in order to raise
in order to raise 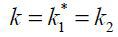 . For a stand-alone firm, the feasible capital in production k is determined by the following equation.
. For a stand-alone firm, the feasible capital in production k is determined by the following equation.
Similarly, the set of feasible capital in production for a business group, i.e., 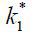 for Firm 1 and k2 or Firm 2, is determined by the following equations.
for Firm 1 and k2 or Firm 2, is determined by the following equations.
By solving for the equations above with 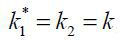 ,
,
where kE is the feasible external equity finance that a stand-alone firm with managerial talent z can raise given kC.
At this point, we can compare the effective degree of financial frictions between
business-group firms and stand-alone firms. By fixing capital in production as 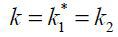 , we observe the ratio of capital in production to private finance for a stand-alone
entrepreneur (SA) and for a business-group entrepreneur (BG) such that
, we observe the ratio of capital in production to private finance for a stand-alone
entrepreneur (SA) and for a business-group entrepreneur (BG) such that
The financial advantage of a business group can then be measured by the following ratio.
This ratio depends both on the cost of building up a subsidiary firm, wM, and the efficiency of external capital markets, (1 − τ)(1 − σ)kE. If the latter outweighs the former, the ratio becomes greater than 1. This implies
that a business group raises more external finance than a stand-alone firm does given
the same amount of private finance. For instance, suppose that 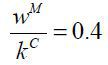 and
and 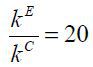 given τ = 0.3 and σ = 0.9. Then, the ratio becomes 2, meaning that a business group k raises twice as
much capital than a stand-alone firm does given the same amount of private finance.
given τ = 0.3 and σ = 0.9. Then, the ratio becomes 2, meaning that a business group k raises twice as
much capital than a stand-alone firm does given the same amount of private finance.
The asymmetric financial advantage of business groups can be lessened if business groups are subject to a lower fraction of equity shares sold to outside shareholders such that σBG < σSA. With this condition, the above ratio can be rewritten as follows.
Given the same specification as above but with σBG = 0.87 and σSA = 0.9, we can observe that the ratio becomes 1.01 and the asymmetric financial advantage of business groups is almost nullified. This teaches us that the minimum equity shares (1−σBG) which the controlling shareholder of a business group should keep to control over the business group can have sizable effects on mitigating the asymmetric financial advantage of business groups. However, note that this example is devised for a stark comparison and that business-group entrepreneurs can choose z2 and optimize their external financing. Thus, we can guess that σBG should be much lower in order to lessen the asymmetric financial advantage of business groups in equilibrium.
B. Asymmetric Financial Frictions
Given the finite amount of capital stock in an economy, the asymmetric financial advantage of business groups is in other words the asymmetric financial frictions between business-group firms and stand-alone firms, which can result in factor misallocation in a general equilibrium. Note that managerial compensation wM is a certainty equivalent proportional to the firm’s expected cash flow net of risk premium while external equity finance kE can grow more rapidly than wM and that (1 − τ)(1 − σ)kE can grow much more rapidly than wM. Thus, the improvement of investor protection captured by a declining τ can increase the gap of external finance raised by business-group firms and stand-alone firms.
The asymmetric financial frictions are of concern because it can be another source of factor misallocation. In equilibrium, alleviated financial frictions for business groups can increase the demand for external capital and push up the price of capital. For stand-alone firms, however, the higher price of capital r acts as a higher degree of financial frictions τ in that the financial constraints of external finance always come with 1/(1+r) as well as (1−τ) . Thus, given the lack of internal capital markets with the higher price of capital, stand-alone firms cannot raise as much capital as they could in an economy without business groups. As a result, an economy with business groups can give rise to a higher price of capital and lower aggregate output due to factor misallocation. Moreover, given that the asymmetric financial frictions between business-group firms and stand-alone firms are intensified as the degree of financial frictions are mitigated, we can guess that the costs of business groups are more likely to dominate their benefits in equilibrium as financial frictions decrease. Last but not the least, the financial advantage of business groups increasing with investor protection (1−τ) implies that the prevalence of business groups needs not attenuate as investor protection improves.
C. External Finance Substituting for Private Finance
As the degree of financial frictions τ decreases, the model shows that both the volume of external equity finance kE and corporate savings, or corporate lending −kD , can expand without increasing capital in production k. Suppose that firms are financially unconstrained and that the degree of financial frictions is lessened such that
From Corollary 2, we find that a business-group entrepreneur can be better off by
increasing consumption dc > 0 and decreasing both private finance 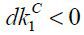 and external debt finance
and external debt finance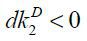 without altering the next-period wealth da′ = 0 such that
without altering the next-period wealth da′ = 0 such that
Note that a decrease in private finance 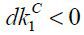 without a change in capital in production
without a change in capital in production 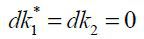 means a larger amount of net external finance such that
means a larger amount of net external finance such that
Moreover, from Corollary 2 with dk2 = 0, we can observe that internal equity finance 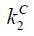 increases with corporate savings
increases with corporate savings 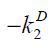 such that
such that
Similarly, from Corollary 1, a stand-alone entrepreneur can be better off by increasing consumption dc > 0 and decreasing both private finance dkC < 0 and external debt finance dkD < 0 without altering the next-period wealth da′ = 0 such that
A decrease in private finance dkC < 0 without a change in capital in production dk = 0 means a larger level of net external finance such that
These results show that an excessive amount of external equity finance can be reinvested through corporate savings for risk sharing. In the case of business groups, a parent firm’s excessive external finance flows into its internal equity finance that is used by the subsidiary firms when they invest for risk sharing. Moreover, by raising more external finance, an entrepreneur can reduce wealth transferred to her firm, consume more, and save less. The declining savings ratio of the rich, most of whom are financially unconstrained business-group entrepreneurs, can result in a decline in the capital stock of an economy. Thus, in the model, the strictly positive correlation between the price of capital and aggregate capital in production of an economy can be broken as financial frictions decrease.
VI. A Numerical Example of the Model
A. Setup
I construct a numerical example of the model and use it to compare two economies: an economy with business groups in which an entrepreneur can choose to create a business group and an economy without business groups in which building a business group is not an option for an entrepreneur.
Table 1 summarizes the parameters used in the numerical example. A CRRA utility function
is employed such that 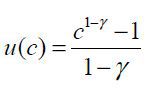 . I choose parameters that are conventional in the literature with one exception,
a time-discounting factor β, which is intentionally set to a very low value for rapid convergence of the numerical
calculation. Model-specific parameters such as flotation costs and maximum equity
shares sold to outside shareholders are based on the rule of thumb.12
. I choose parameters that are conventional in the literature with one exception,
a time-discounting factor β, which is intentionally set to a very low value for rapid convergence of the numerical
calculation. Model-specific parameters such as flotation costs and maximum equity
shares sold to outside shareholders are based on the rule of thumb.12
The wealth space is discretized into twenty exponentially increasing grids from a(1) =1.0×10−4 to a(20) =1.0×106. The managerial talent space is discretized into twenty exponentially increasing grids from z(1) =1 to z(20) = 4. The transition probability of the managerial talent from z = z(i) to z′ = z(j) is defined as follows: ∀i∈{1, 2,⋯, 19, 20}, j = max{1, min{20, i+k}} with probability pk, k ∈{−9, −8, ⋯,8, 9}, in Table 2.13
Lastly, I assume that the capital depreciation rate δ′ is a simple random variable, which is independent of shocks to managerial talent such that
B. Observations
Observation 1 (Occupational Choice). The rich choose to become business-group entrepreneurs. The poor but talented are hired as business-group managers with positive probabilities. The northwest region of (z,a), where individuals with positive probabilities of being hired as managers reside, becomes smaller as investor protection improves. The poor, untalented become workers.
Figure 3 shows the occupational choices of individuals given a moderate degree of financial frictions, τ = 0.5. We find that the east, where the rich reside, is filled with business-group entrepreneurs and that the northwest, where the poor but talented reside, is filled with stand-alone entrepreneurs who can be hired as business-group managers. This occupational policy function shows that pyramidal business groups work as start-up breeders that can foster productive firms given capital market imperfections. In the southwest, a declining line separating a SA region from a W region indicates that wealth is required for an individual to become a stand-alone entrepreneur given financial frictions.
FIGURE 3.
OCCUPATIONAL MAP IN AN ECONOMY WITH BUSINESS GROUPS GIVEN τ = 0.5
Note: No population exists outside the border of the orange line.
As the fraction of diversion decreases to τ = 0.1, two changes are observed in Figure 4 below, which depicts the occupational choices of individuals in an economy with business groups given τ = 0.1. First, the rich but untalented still become business-group entrepreneurs because they expect to earn ex-ante positive profits by hiring the talented as managers. We will see that these unproductive business-group entrepreneurs can be a source of resource misallocation. If we shut down the possibility of creating pyramidal business groups, the southeast region in Figure 6 shows that the rich but untalented business-group entrepreneurs would become workers in an economy without business groups given τ = 0.1.
Second, Figure 4 shows that fewer individuals are hired as business-group managers. Note that the managerial compensation wM (z2,a2) is likely to increase as financial frictions decrease because an outside option of running a stand-alone firm should be a better option with lower financial frictions. Thus, business-group entrepreneurs must hire the more talented but still financially constrained in order to earn positive profits. The contracted upper northwest region in Figure 4 captures this rising cut-off value of managerial talent, which can give business-group entrepreneurs positive profits with high enough managerial talent but low enough managerial compensation.
FIGURE 4.
OCCUPATIONAL MAP IN AN ECONOMY WITH BUSINESS GROUPS GIVEN τ = 0.1
Note: No population exists outside the border of the orange line.
FIGURE 5.
OCCUPATIONAL MAP IN AN ECONOMY WITHOUT BUSINESS GROUPS GIVEN τ = 0.5
Note: No population exists outside the border of the orange line.
Observation 2 (The Relative Number of Business-Group Firms). The prevalence of business groups shows an insignificant correlation with the strength of investor protection as measured by (1−τ). Specifically, the relative number of business-group firms out of all corporations does not decrease with (1−τ).
Observation 2 can be understood as a corollary of Observation 1, which states that the rich become business-group entrepreneurs regardless of the degree of financial frictions. Figure 7 below presents two interesting features about the prevalence of business groups. First, business-group firms cannot thrive under overly severe financial frictions, such as τ ≥ 0.7, because overly severe financial frictions undermine the financial advantage of a pyramidal ownership structure that leverages external capital markets.
Second, although the total number of business-group firms is unvarying, the number of subsidiary firms decreases as financial frictions decrease. Observation 1 already shows that the number of individuals who have a positive probability of being hired as managers decreases as financial frictions decrease. We will observe in the following observations that subsidiaries are more productive than parents and that this decreasing ratio of subsidiary firms can weaken the benefits of pyramidal business groups as start-up breeders.
Observation 3 (Asymmetric Financial Frictions between Business-Group Firms and Stand-Alone Firms). Business-group firms have a larger ratio of capital to labor than stand-alone firms. The variance of the capital-to-labor ratios is smaller within business-group firms than within stand-alone firms.
Given the Cobb-Douglas production function, the ratio of capital to labor would be identical for all types of firms if an economy had no financial frictions and no shocks to managerial talent. Thus, business-group firms’ higher mean and smaller variance of the capital-to-labor ratios suggest that business-group firms have better financial conditions than stand-alone firms. Figure 8 shows that these instances of asymmetric financial frictions persist and hardly vary even when investor protection improves.
Figure 8 also shows that public corporations achieve capital-to-labor ratios nearly identical to those of business groups as τ goes to zero. This implies that firms would be financially unconstrained if they could use external equity finance with fine investor protection. However, the asymmetric financial frictions between the business-group and the stand-alone firms do not wane because most standalone entrepreneur do not pay flotation costs kF and turn down the option of tapping into external equity markets. As indicated in Figure 7, most corporations are business-group firms, and the relative number of public corporations using external equity finance decreases as τ decreases.
Then, the question is if this asymmetric financial frictions have sizable effects on resource allocation. The following Observation 4 provides an answer to this question.
Observation 4 (Firm Size Distributions). Business-group firms have a larger mean and variance of employment and also have a larger mean and variance of TFP than stand-alone firms.
Figure 9 shows that business-group firms are larger than stand-alone firms on average because business-group firms have not only better financial conditions (Figure 8) but also better managerial talent on average (Figure 10).
Business-group firms, however, also have larger variances of employment and managerial talent. Given the persistence of asymmetric financial frictions, a large number of unproductive business-group firms can distort resource allocation in a stationary equilibrium. Note that the distributions of business-group firms are bimodal. Small, unproductive business-group firms coexist with large, productive business-group firms. This observation complies with the occupational choice that the rich but unproductive choose to become business-group entrepreneurs regardless of the degree of financial frictions (Figure 4).
Given that pyramidal business groups have a financial advantage but also have more dispersed productivities, the effects of pyramidal business groups on resource allocation are ambiguous. Their financial advantage makes business-group firms not only raise more capital but also allocate more capital to low-productivity business-group firms. Observation 5 below shows that the net effects of pyramidal business groups depend on the level of financial frictions, τ.
Observation 5 (Factor Prices and Aggregate Inputs). As the strength of investor protection (1−τ) improves in an economy with business groups, both the rate of return on capital and wages increase monotonically, while both the capital stock and labor force increase first and then decrease.
Figure 11 captures the correlations between factor prices and aggregate inputs with regard to the degree of financial frictions. It shows that positive correlations between factor prices and aggregate inputs are broken under the prevalence of business groups. The existence of business groups helps an economy achieve a large amount of aggregate input under a moderate level of financial frictions, such as τ ∈ [0.3, 0.7]. However, a further decrease in financial frictions from τ = 0.2 only pushes up factor prices and results in relatively less aggregate input of an economy. This non-monotonicity contrasts with the strictly positive correlations between factor prices and aggregate inputs in an economy without business groups.
The negative correlation observed in Figure 11 derives from a decrease in savings of the rich. Table 3 below captures savings of the rich,14 whose wealth is in the top 0.14% in an economy with business groups. It shows that the rich who choose to create business groups save less as financial frictions decrease. Their level of savings decreases from 0.88 to 0.53, and the share of their savings decreases from 52% to 33%. This decrease in savings can be supported by the financial advantage of business-group entrepreneurs, which allows them to substitute external finance for private finance. With the same amount of wealth, business-group entrepreneurs can consume more and save less by raising more external capital as financial frictions decrease.
It is interesting that the savings of the rich would monotonically increase with investor protection if we shut down the possibility of creating business groups. In an economy without business groups, the savings of the rich increase from 35% to 47% as financial frictions decrease from τ = 0.5 to τ = 0.1. Note that the population of the rich increases,15 which implies that the lower level of financial frictions help the talented accumulate wealth in an economy without business groups.
In an economy dominated by business groups, however, its stagnating population of the rich suggests that the poor but talented suffer from asymmetric financial frictions and have difficulty in accumulating wealth. Table 4 shows this possibility. The absolute level of stand-alone entrepreneurs’ wealth decreases from 1.04 to 0.46 as financial frictions decrease from τ = 0.5 to τ = 0.1, and the share of their wealth also decreases from 40% to 18%. Note that the population of stand-alone entrepreneurs scarcely changes as financial frictions decrease. This implies that the decrease in stand-alone entrepreneurs’ wealth derives from a decrease in their wealth on average, not from a decrease in their overall population.
Observation 6 (Aggregate Flotation Costs). An economy with business groups consumes larger flotations costs than an economy without business groups.
Observation 6 teaches us that creating a business group can be an efficient choice for an individual, but not for an economy. As shown in Figure 12, the flotation costs of an economy with business groups increase more rapidly than those of an economy without business groups. Recall that the rich but untalented create business groups by paying flotation costs in order to launch productive subsidiaries. Thus, incorporating pyramidal business groups requires larger fixed costs. The problem is that while more parent firms are incorporated, fewer subsidiary firms are launched as financial frictions decrease.
Figure 13 shows that the aggregate flotation costs in an economy with business groups are sizable. The aggregate investment net of flotation costs decreases as τ goes to zero. This is in good agreement with the observation that as τ goes to zero, the capital stock of an economy with business groups declines.
One can ask why net investment declines despite the fact financial frictions decrease and the rate of return on capital continues to rise. Figure 14 gives an explanation. It shows that the investment rate of an economy with business groups is not only larger than that of an economy without business groups but that it also increases monotonically. Thus, a decrease in financial frictions indeed increases the investment rate of an economy. The excessive flotation costs used up by business groups, however, overwhelm the increase in investment and result in the decrease in net investment used for replenishing capital depreciation in a stationary state equilibrium as τ goes to zero.
Observation 7 (Aggregate Output). We define the aggregate output of an economy as the sum of aggregate consumption and aggregate investment. The aggregate output of an economy with business groups thus does not monotonically increase with investor protection. When the level of investor protection is strong enough, such as (1−τ) ≥ 0.8, an increase in investor protection does not increase the aggregate output of an economy under the prevalence of business groups.
Pyramidal business groups cause the aggregate output of an economy to regress toward a moderate level over the degree of financial frictions. Figure 15 shows that business groups can partially nullify the impact of financial frictions on aggregate output. At an early stage of development, where financial frictions are rampant, business groups help an economy produce larger levels of aggregate output.16 When the tunneling ratio τ goes to zero, however, Figure 15 shows that the aggregate output of an economy with business groups stagnates.
Observation 7 rebuts the argument that the economic impact of business groups would spontaneously vanish if investor protection improves. The stagnating aggregate output rather suggests that achieving good investor protection is not enough to lessen the effects of business groups on an economy and that aggregate output may not grow without restraining the prevalence of business groups. As argued earlier, business groups can asymmetrically benefit from an improvement of investor protection in the model. The stagnating aggregate output of an economy with business groups in Figure 15 suggests that the asymmetric financial frictions become sizable and that the benefits of business groups can be dominated by their costs when the degree of financial frictions is low enough, such as τ ≤ 0.2.
The following Observation 8 shows how sizable the asymmetric financial frictions between the business-group and the stand-alone firms are and why dealing with the pyramidal ownership structure is necessary for the development of external capital markets.
Observation 8 (External Capital Markets). We define the size of external capital markets as the sum of external debt finance and external equity finance used by all firms such that
Controlling for aggregate output, the external capital markets of an economy with business groups are smaller than those of an economy without business groups.
Figure 16 shows that the underdevelopment of external capital markets can be associated with the prevalence of business groups in equilibrium. However, this does not mean that shutting down business groups increases the sizes of external capital markets. External capital markets of an economy with business groups are larger than those of an economy without business groups given a moderate degree of financial frictions τ∈[0.3, 0.6], while they are smaller given a low degree of financial frictions τ ≤ 0.2. 17 It is a more precise interpretation of the result that business groups decrease the size of external capital used by stand-alone firms in equilibrium. Figure 16 shows that more than half of external capital is used by business groups and that the external capital used by stand-alone firms is smaller than that by their counterparts in an economy without business groups.
This underdevelopment of external capital markets in an economy with business groups arises due to the asymmetric financial frictions between business-group firms and stand-alone firms in the model. Note that given the same degree of financial frictions, the price of capital is always higher in an economy with business groups than in one without business groups. The higher price of capital impairs stand-alone firms’ external financing. Thus, stand-alone firms, which lack internal capital markets, should suffer from tighter financial constraints and cannot but raise less external capital in an economy dominated by business groups.
VII. Concluding Remarks and Future Research
Financial frictions can cause resource misallocation. It is understood as one of the major hindrances to economic development. Although many researchers have shown why and to what extent financial frictions can affect an economy, few macroeconomic models have investigated private institutions that can arise as endogenous reactions against financial frictions. In this paper, I study the endogenous creation of pyramidal business groups and focus on the repercussions of their financial advantage given capital market imperfections.
There are three main implications of the model. First, pyramidal business groups can be efficient private institutions if external capital markets are underdeveloped due to severe financial frictions. Second, the asymmetric financial frictions between business-group firms and stand-alone firms can create inefficiencies that impair stand-alone firms’ external financing in equilibrium. Third, the prevalence of business groups does not spontaneously shrink as investor protection improves.
The final implication can be viewed as a limitation of this paper, in that the unvarying number of business-group firms in the model cannot explain why the prevalence of business groups differs across developed countries. Thus, finding a rationale for the cross-country difference can be an interesting topic for future research. For instance, Kandel, Kosenko, Morck, and Yafeh (2015) argue that U.S. pyramidal business groups have almost disappeared because the U.S. government pursued specific policy measures to regulate business groups, such as the Public Utility Holding Company Act (1935), and the increase in inter-corporate dividend taxation (after 1935). We can use the model developed in this paper to conduct a counter-factual analysis that examines how effectively the regulations adopted in the U.S. can reduce the prevalence of business groups and undo the factor misallocation spawned by the business groups.
Another follow-up research agenda can be to study the effects of pyramidal business groups on wealth inequality and socioeconomic mobility. The model developed in this paper suggests that the rich can entrench their wealth by building up pyramidal business groups, which results in a decrease in the probability of the poor accumulating wealth. Given the assumption that the inequality of entrepreneurial productivity stems from luck, business groups could be an institution that allows the rich to insure their wealth against their bad luck. This entrenchment of the rich implies that the prevalence of business groups can prevent the poor from exploiting their good luck in a general equilibrium. Thus, the model could be used to study how pyramidal business groups can change the patterns of wealth inequality and socioeconomic mobility.
Notes
This paper is a revised version of Cho (2016). I am grateful to Yongseok Shin for his guidance. This research is benefited from discussion with Gaetano Antinolfi, Costas Azariadis, Kee Youn Kang, Minho Kim, Yoonsoo Lee, Rodolfo Manuelli, Bruce Petersen, B. Ravikumar, and seminar participants at the 2015 European Winter Meeting of the Econometric Society, 2017 KAEA Annual Meeting, Washington University in St. Louis, Chungang University, Sogang University, and Yonsei University. Thanks to two anonymous referees for valuable comments. All errors are mine.
La Porta, Lopez-de Silanes, and Shleifer (1999) examine 27 wealthy countries and show that most of the largest corporations in a country are business groups controlled by families or the state through pyramidal ownership schemes. La Porta, Lopez-de Silanes, Shleifer, and Vishny (2000) argue that the degree of investor protection is closely related to the corporate governance structure and that business groups are common in countries with poor investor protection. Masulis, Pham, and Zein (2011) examine 28,635 listed firms in 45 countries, including developing economies, and reaffirm that pyramidal business groups are a common ownership structure around the world. They show that the prevalence of business groups is negatively associated with the capital availability of an economy, but insignificantly associated with the degree of investor protection. They argue that business groups emerge in order to alleviate financial frictions.
As of 2004 in South Korea, business groups controlled by a few families hold 56% of the market capitalization in the country according to Masulis, Pham, and Zein (2011).
Given that a business group is a dominant ownership structure of the largest corporations in a country, this study revisits a question raised by many others: does the size distribution of firms in a country affect its economic efficiency?
Note that a common implementation of financial frictions in the literature hinges on an out-of-equilibrium path and that such a diversion does not occur in equilibrium (e.g. Buera, Kaboski, and Shin, 2011).
An exogenous process of managerial talent can be understood as a parsimonious means of capturing the impact of financial frictions on factor allocation by abstracting away from the endogenous nature of managerial talent. In Section 6, I will specify a state space and a transition probability of managerial talent z.
We can think of this timing structure, raising 𝑘 given 𝑧 and then producing cash flow 𝜋 after observing 𝑧′, as the risk an entrepreneur takes when making investment decisions.
I use (𝑧1, 𝑎1) instead of (𝑧, 𝑎) because (𝑧1, 𝑎1) is convenient for comparing a parent's managerial talent 𝑧1 indexed by 1 to a subsidiary's managerial talent 𝑧2 indexed by 2.
Figure 2 is not the equilibrium output of the model. It is an example constructed to clarify the idea of an individual's occupational choice problem.
The fraction of diversion, τ, is a parsimonious modeling device capturing the economy-wide degree of financial frictions in order to focus on macroeconomic implications. Detailed practices from which financial frictions arise are abstracted in the model. Due to this lack of a microeconomic structure, the model is silent with regard to how an entrepreneur can divert her firm’s cash flow. Diversion in the model can therefore be interpreted as a wide variety of microeconomic limited commitment problems in the real world, such as agency costs during the managerial pursuit of private benefits (Jensen and Meckling, 1976) or tunneling practices of transferring resources (Johnson et al., 2000). Thus, τ or (1-τ) is interchangeably labeled throughout this study, i.e., the degree of financial frictions, tunneling, investor protection, or the rule of law.
kF captures expenses such as underwriting fees, legal fees, or registration fees of issuing shares. Although in the real world flotation costs consist of fixed costs as well as costs proportional to the extent of shares issued, only the fixed costs are employed in the model with kF. I exclude the proportional costs that can be paid with external financing after issuing shares because the efficiency of these back-loaded costs is scarcely distinguishable from the degree of financial frictions 𝜏. Moreover, in the model, kF is paid every period if an entrepreneur runs a publicly held corporation successively.
For example, I choose σBG = 0.7 because it is one of the criteria the Fair Trade Commission in South Korea uses to identify if a corporation is a business-group subsidiary.
Note that given the exponentially increasing managerial talent space, the transition probability defined in Table 2 mimics a scale-free growth process bounded below 𝑧′ = 𝑧(1) with negative drift, which can approximate a stationary Pareto distribution (e.g., Gabaix, 1999).
I choose 𝑎(13) = 398 as the criteria for the rich because the population of individuals whose wealth is greater than or equal to 398 hardly changes as financial frictions decrease; the population changes from 0.147% with 𝜏 = 0.5 to 0.136% with 0.136%.
Given the criteria of the rich, 𝑎 ≥ 𝑎(13) = 398, the population of the rich in an economy without business groups increases from 0.11% with 𝜏 = 0.5 to 0.21% with 𝜏 = 0.1.
Figure 15 shows that a little development of investor protection is required for business groups to help an economy produce more aggregate output. This arises because the internal equity finance of business groups works as leverage for raising capital from external markets. Excessive financial frictions can weaken the efficiency of the financial advantage of pyramidal business groups.
References
, & . (2006a). Should business groups be dismantled? the equilibrium costs of efficient internal capital markets. Journal of Financial Economics, 79(1), 99-144, https://doi.org/10.1016/j.jfineco.2005.02.001.
, & . (2006b). A theory of pyramidal ownership and family business groups. The Journal of Finance, 61(6), 2637-2680, https://doi.org/10.1111/j.1540-6261.2006.01001.x.
, & . (2013). Pyramidal ownership and the creation of new firms. Journal of Financial Economics, 108(3), 798-821, https://doi.org/10.1016/j.jfineco.2013.01.009.
, , & . (2011). Finance and development: A tale of two sectors. American Economic Review, 101(5), 1964-2002, https://doi.org/10.1257/aer.101.5.1964.
. (1999). Zipf’s law for cities: an explanation. The Quarterly Journal of Economics, 114(3), 739-767, https://doi.org/10.1162/003355399556133.
, & (1976). Theory of the firm: Managerial behavior, agency costs and ownership structure. Journal of Financial Economics, 3(4), 305-360, https://doi.org/10.1016/0304-405X(76)90026-X.
, , , & . (2000). Tunneling. American Economic Review, 90(2), 22-27, https://doi.org/10.1257/aer.90.2.22.
, & . (2007). Business groups in emerging markets: Paragons or parasites? Journal of Economic Literature, 45(2), 331-372, https://doi.org/10.1257/jel.45.2.331.
, , & . (1999). Corporate ownership around the world. The Journal of Finance, 54(2), 471-517, https://doi.org/10.1111/0022-1082.00115.
, , , & . (2000). Investor protection and corporate governance. Journal of Financial Economics, 58(1), 3-27, https://doi.org/10.1016/S0304-405X(00)00065-9.
, , & . (2011). Family business groups around the world: financing advantages, control motivations, and organizational choices. The Review of Financial Studies, 24(11), 3556-3600, https://doi.org/10.1093/rfs/hhr052.
. (2014). Productivity losses from financial frictions: Can self-financing undo capital misallocation? The American Economic Review, 104(10), 3186-3221, https://doi.org/10.1257/aer.104.10.3186.
, , & . (2005). Corporate governance, economic entrenchment, and growth. Journal of Economic Literature, 43(3), 655-720, https://doi.org/10.1257/002205105774431252.
. (2015). Financial frictions, internal capital markets, and the organization of production. Review of Economic Dynamics, 18(3), 505-522, https://doi.org/10.1016/j.red.2014.10.001.