
- P-ISSN 2586-2995
- E-ISSN 2586-4130

This paper examines the empirical magnitude of local human capital spillovers in Korea during the 1980s and mid-1990s. Local human capital spillovers exists if plants in regions with a higher level of human capital can produce more given their own amount of input (Moretti 2004c). In particular, this paper explores an educational reform in South Korea which exogenously induced a large amount of variation in regional human capital levels. Using annually collected plant level data, I explore the effect of changes in the regional human capital levels induced by this reform on plant productivity in Korea. My results suggest that this effect is limited. I find a positive correlation between a regional level of human capital and plant productivity. However, after further addressing endogeneity using an instrumental variable, the effect of the overall regional human capital level on productivity decreases and becomes statistically insignificant.
Local Human Capital Spillovers, Plant Productivity, Instrumental Variable, College Education, South Korea
J24, I20, O40
Human capital externalities have been considered as a major source of economic growth and are thus of interest to both economists and policymakers (Lucas 1988). Hence, many theories suggest possible mechanisms that can lead to human capital externalities. Local human capital spillover, which involves face-to-face interaction among individuals, is argued by many as a main source of human capital externalities. This idea goes back at least to Marshall (1890) and was more recently suggested by Arrow (1962) and Romer (1986). According to this view, geographical proximity between workers is an important condition for human capital spillover, as exchanges of ideas through personal interaction is assumed to decrease with distance. This view of the mechanism of human capital spillover has been used to argue for the importance of cities as engines of economic growth (Jacobs 1970). The literature proposing local human capital spillover suggests that worker productivity will be positively affected by the human capital of other workers within the geographical region through personal interactions between workers that may lead to human capital spillover. Thus, local human capital spillover implies that a plant in a region with a higher level of human capital could produce a greater given human capital level of their own workers. In other words, local human capital spillover exists if the productivity of the plant is positively affected by the human capital level in other plants located nearby (Moretti 2004c).1
The main purpose of this paper is to examine the empirical extent of local human capital spillover in the context of Korea during the 1980s and early 1990s. Specifically, I provide new evidence of the magnitude of local human capital spillover in Korea using plant productivity. In particular, I closely follow the methodology of Moretti (2004c), a study which uses plant-level data to provide evidence of the magnitude of local human capital spillover in the U.S. This paper adds to the literature by exploring the role of spillover through personal interactions in the context of a (then) developing country. In particular, despite the widespread belief regarding the importance of human capital externalities in the growth of South Korea—e.g., Lucas (1988, 1993)—little is known about the empirical importance of local human capital spillover as a potential channel for the externalities. My results suggest the local human capital spillover through face-to-face interactions between workers beyond plant boundaries may not have been a crucial factor in Korea’s growth during the 1980s and 1990s.
In 1980, the Korean government implemented an educational reform that resulted in a large and discrete increase in the number of students entering college in 1981. As a result of this discrete increase in freshmen enrollment, there was a large increase in the supply of college graduates, which induced an increase in the proportion of the college graduates in the workforce. Exploiting this variation, I examine the extent of local human capital spillover in Korea. Furthermore, I propose an instrumental variable based on the implementation of the reform to examine further the potential for endogeneity in levels of cross-regional variance in human capital.
I implement this idea using 1982-1996 data from the Mining and Manufacturing Survey, as collected by Statistics Korea. The data provide detailed information on output, labor and capital, and other plant-specific characteristics such as ownership type, age, industry and location. In particular, by estimating a production function at the plant level, I examine whether region-specific increases in the share of college graduates had a positive effect on plant productivity after controlling for plant-specific inputs and characteristics. Specifically, investigating the extent of local human capital spillover based on plant-level data could be particularly useful in the context of Korea, where the size of the country is compact compared to countries such as the U.S. or China. That is, although Korean workers could move across regions within a country with relatively little cost, it is costly to relocate an establishment. Thus, using plants of which the location is most stationary would be more suitable for exploring whether productivity is affected by regional characteristics.
Overall, I do not find supportive evidence of the presence of local human capital spillover. In other words, after controlling for the plants’ own levels of human capital, the proportion of workers with a college education in a given region does not have a meaningful effect on a plant’s productivity. The magnitude of the simple correlation between the regional level of human capital and plant productivity is similar to that observed using plant level data in the U.S. In particular, pooled regressions suggest that a one percentage point increase in the proportion of college graduates in a region is associated with a 0.7 percentage increase in productivity. However, after instrumenting for the human capital level, the effect is reduced and becomes statistically insignificant. The results from the instrumental variable analysis show that there is positive bias in the correlation between the level of human capital and productivity. Overall, the findings of the paper are in line with recent work by Huber (2012) which questions the presence of human capital spillover beyond establishment boundaries. In particular, by surveying workers in a R&D complex in England, he finds that they have limited interactions with workers outside their establishment. This may also be true in South Korea; specifically, given the long working hours in Korea during the 1980s and early 1990s, workers would have had limited time to interact with workers outside of their plants.
As stated earlier in this section, several papers examine the empirical extent of local human capital spillover. Other work documents the positive relationship between productivity and average years of schooling using cross-country data (de la Fuente and Domenech 2001). However, cross-country evidence is unlikely to reveal the magnitude of human capital externalities given that the average levels of human capital are likely correlated with characteristics that can affect productivity (Hall and Jones 1999). To overcome this shortcoming, some papers exploit arguably an exogenous variation using city- or state-level data. Overall, empirical evidence in the existing literature is mixed. For instance, Rauch (1993) and Moretti (2004a) find positive and sizable local human capital spillover on productivity, whereas Acemoglu and Angrist (2000) and Rudd (2000) find little evidence that these spillovers are significant in practice. Most papers document human capital externalities by comparing the wages of workers across regions with different levels of human capital.2 Acemoglu and Angrist (2000) exploit state variations in compulsory schooling laws to analyze the effect of the average human capital in a state on workers’ productivity; they find little evidence of externalities from of K-12 education. Moretti (2004a), on the other hand, uses the proportion of college graduates as a measure of the average human capital in a region and finds significant increases in wages associated with an increase in the share of college graduates. Iranzo and Peri (2009) reconcile the result from Acemoglu and Angrist (2000) and Moretti (2004a). In particular, these authors argue that the magnitude of externalities from college education could be greater than those from secondary education. Ciccone and Peri (2006) use an alternative method to address the possibility that the use of the Mincerian equation in earlier studies could bias results toward finding a human capital externality. They find no evidence of externalities from average schooling at the city or state level in the U.S.
Moretti (2004c) examines the effect of the share of college graduates on productivity using plant-level data. His idea is that, if local human capital spillover exists, workers in a region with a higher level of human capital will be more productive and thus the plants hiring those workers would be more productive. Specifically, combining the manufacturing censuses of 1982 and 1992 with the population censuses of 1980 and 1990, he finds that the plants located in cities with high levels of human capital produce greater amounts of output with the same amount of input than otherwise similar plants located in cities with low levels of human capital. In particular, the result shows that a one percent point increase in the fraction of college graduate workers in a given region leads to a 0.5 - 0.7 percent increase in productivity.
The rest of this paper is organized into the following sections. Section II introduces the institutional background and Section III describes the data. Section IV presents the identification strategy. Section V presents results and a series of robustness checks. The last section discusses the conclusion.
Korea offers a unique institutional setting for this type of study in that the central govern- ment controls the supply of college graduates by setting the freshmen quota, or entrance quota, for both private and public colleges.3 The freshmen quota was strictly enforced during the 1970s and 1980s, as colleges faced severe penalties for admitting freshmen beyond the assigned quota, such as a loss of government funding and a decrease in their quotas for the following years.4 Moreover, the government controlled the number of colleges by granting permission for the establishment of new institutions. The number of colleges remained essentially stable across regions during the period of interest.5 In short, this setting was quite different from those in countries such as the U.S., in which college enrollment is not set in a centralized manner. Owing to the way in which college enrollment was determined in Korea, the supply of college education was less likely to be responsive to time-varying region-specific characteristics.
Until 1980, the government only allowed a gradual increase in the freshmen quota despite a large increase in the demand for college education in the 1970s. As a result, the number of ‘repeat applicants’, referring to who were forced to apply to colleges for more than one year to receive higher education, accumulated as the quota was not sufficient to accommodate all of the students who wanted to enter college.
However, in 1981, the freshmen quota discretely jumped due to an unexpected education reform announced on July 30, 1980 (Choi 1996).6 The main purposes of the reform were to: i) increase the probability that students from disadvantaged backgrounds would receive a college education, and ii) reduce the number of ‘repeat applicants’. The major component of the reform was a discrete increase in the freshmen quota to accommodate more students.7 Figure 1 describes the mandated increase in the freshmen quota and the corresponding increase in freshmen enrollment in 1981 as stipulated in the reform. It is clear that this large increase was a one-time event, as the freshmen quota was stable during the 1980s after the initial increase in 1981.
Note: The solid blue circles in the figure describe the trend in the number of actual number of freshmen biannually during the period between 1971 and 1987. The hollow red dots represent the planned number of freshmen, i.e., the freshmen quota, during the corresponding period.
Importantly, the central government forced each and every college to increase the freshmen quota in essentially the same manner. That is, the magnitude of the increase was not endogenously adapted to each college to accommodate the region-specific demand for higher education. In particular, the implementation of the increase in the freshmen quota was more or less mechanical—in general, the government set the freshmen quota in 1981 for each college in proportion to the freshmen quota of previous years. Thus, colleges which happened to have a large freshmen quota in 1979 experienced larger absolute increases by 1981. Figure 2 plots the freshmen quota for each college in 1979 and 1981 along with a 45-degree line. This figure shows that the relationship between the freshmen quotas in 1981 and in 1979 is linear, suggesting that the freshmen quota in 1979 primarily determined the increase. The figure also shows that the absolute differences in the enrollment increase, the gap between the 45-degree line and the freshmen quota in 1981, increase as the initial freshmen quota increases.
Note: The solid blue circles in the figure describe the correlation between the freshmen quota in 1979 and that in 1981 at the college level. The solid green line is the linear fit between the freshmen quota in 1979 and that in 1981. The red line is a 45-degree line included as a reference.
Because the reform was consistently applied to each college, the relationships between the freshmen quota in 1979 and that in 1981 in each region are similar. Figure 3 describes the correlation between the freshmen quotas in 1979 and in 1981 in each region along with a 45-degree line. By comparing the freshmen quota in 1981 with the 45-degree line, it becomes clear that regions which happened to have higher freshmen enrollment in 1979 experienced larger absolute increases by 1981. Thus, the reform exogenously increased the difference in the supply of college graduates in each region after the mid-1980s. Furthermore, this figure confirms that the freshmen quota in 1981 in each region was indeed mostly determined by the proportional increase in the freshmen quota in 1979—the relationship between the quotas in 1979 and in 1981 is linear. The figure thus provides evidence which refutes the claim that the increase in the freshmen quota in 1981 was endogenously determined by the government.
Note: The solid blue circles in the figure describe the correlation between the freshmen quota in 1979 and that in 1981 at the college level. The solid green line is the linear fit between the freshmen quota in 1979 and that in 1981. The red line is a 45-degree line included as a reference.
As a result of the education reform, there was a large increase in the supply of college graduates, which induced a rapid increase in the proportion of college graduates among the workforce. More importantly, there was a large degree of arguably exogenous variation in terms of the increase in the proportion of college graduates across the regions after the mid-1980s. I use this regional variation in the impact of the reform to identify the magnitude of local human capital spillovers.
To examine local human capital spillover using plant productivity, I use the Mining and Manufacturing Survey provided by Statistics Korea. Statistics Korea has been collecting these data since 1968, but the micro-data have only been available since 1982. Moreover, because the manufacturing sector of Korea was heavily affected by the Asian financial crisis in 1997, I only use data prior to 1997. These data were collected annually from mining and manufacturing plants with five or more workers. The survey contains detailed information about individual plants, such as their industry classification, output, production costs, locations, and tangible assets including capital.
The data also contain information on the total number of employees and the number of white-collar (non-production) employees. However, like most plant-level data, there is no information on the educational attainment levels of the workers. Thus, I proxy the change in the proportion of college graduates using the change in the proportion of white-collar workers.
To explore the validity of this proxy, I use the Basic Wage Structure Survey. These data have been collected by the Ministry of Employment and Labor of Korea and are designed to represents the wages of workers in establishments with more than ten employees. The survey collects data from individual workers from a sample of establishments representing each sector. The data contain information on wages, education, occupation and industry.8 Using these data, I show that the trend of the proportion of workers with college degrees coincides with the trend of proportion of white-collar workers. Figure 4 displays the share of college graduates and white-collar workers among all workers in the manufacturing sector using the Basic Wage Structure Survey and Mining and Manufacturing Survey. The time trend for white-collar workers tracks the trend of college graduates closely; both trends show a slight increase until the mid-1980s and then start to rise steeply after 1987. Thus, hereafter I use the changes in the proportion of white-collar workers as a proxy for the proportion of college graduates without further distinction.
Note: The solid blue circles in the figure describe the trend in the proportion of the white-collar workers among all workers in the manufacturing sector in the Mining and Manufacturing Survey. The hollow red dots in the graph represent the share of college graduates in the manufacturing sector in the Basic Wage Structure Survey
In my main analysis, I focus on the manufacturing sector in order to ensure a consistent definition of value-added and thus productivity. Additionally, I omit years when the Mining and Manufacturing Survey was conducted as part of the Industrial Census, in this case 1983, 1988 and 1993, as variable definitions and the samples in those years are not consistent with those in other years.
Table 1 provides summary statistics. The first two columns contain the mean and the standard deviation during the period prior to the impact of the reform and columns (3) and (4) describe the corresponding mean and standard deviation of the variables after the impact of the reform. All monetary values are in 1990 Korean Won. One can verify that both the value of the output and the value-added components of individual plants increased rapidly during this period. The average output increased by nearly 50 percent between the two periods, from a base of 2.5 billion won. The average value-added amount of each plant also increased greatly, i.e., by approximately 100 percent.9 Moreover, the average capital stock increased rapidly during the period of interest. The average capital stock of each plant was approximately 723 million won during the years 1982-1986, whereas it was about 1.4 billion won during the years 1987-1996.
Note: Monetary values are in 1990 Korean Won. 1 US dollar is approximately 1,000 Won.
More importantly, the average proportion of white-collar workers increased by a considerable amount. In particular, the average proportion of white-collar workers within a plant increased by nearly 25 percent, or about five percentage points, after the reform went into effect. Moreover, the increase in the proportion white-collar workers did not differ significantly across differently sized plants. The proportion of white-collar workers was approximately 20 percent prior to the impact of the reform for all plant sizes, and about 25 percent after 1987, regardless of the plant size. Consistent with the increase in the proportion of white-collar workers in individual plants, the average proportion of white-collar workers in a given region also increased by a similar amount after the mid-1980s. The average payment to workers increased during this period as the total payment to workers increased by a substantial amount despite the decrease in the number of employees. The average age of an individual plant and the building area used by each plant were both stable during the years 1982-1996. Overall, the summary statistics show that many plant-level characteristics—with a few exceptions—significantly changed with the policy.
In this section, I provide detailed information on how I use this annually collected data to examine human capital spillovers beyond plant boundaries.
The existence of local human capital spillovers implies that plants located in regions with higher levels of human capital will be more productive. Thus, one can assess the magnitude of such spillovers by examining the relationship between the level of human capital and plant productivity in each region. However, empirically estimating externalities is challenging because the change in the level of human capital is endogenous in most cases. That is, unobserved factors affecting regional plant productivity can also have a positive effect on the overall level of human capital. For instance, the establishment of a “million dollar plant” can have a positive effect on the productivity of existing plants and can also attract workers with higher human capital (Greenstone, Hornbeck, & Moretti, 2010). In this case, a positive relationship between the level of human capital in a given region and its average plant productivity could exist even in the absence of human capital externalities. In other words, a positive correlation between the level of human capital and average plant productivity does not necessarily imply the existence of human capital externalities.
In the remainder of this section, I describe the endogeneity issue in detail using an empirical strategy adopted from Moretti (2004c). I also explain how the empirical setting in this paper helps mitigate certain associated concerns. First, I assume a Cobb-Douglas production function;
where Yijrt is output of the plant i, in industry j, in region r, at year t. Bijrt , Wijrt and Kijrt denote the inputs: blue-collar workers, white collar-workers, and capital, respectively. Total factor productivity is represented by Aijrt . If plant productivity depends on the regional level of human capital, then ln Aijrt can be expressed as follows,
where Hrt is the measure of the level of human capital in a given region. In particular, similar to Moretti (2004c), Hrt is the proportion of college graduates in a given region r at time t. The coefficient of Hrt , γ , represents the effect of regional human capital on productivity. Thus, the size of the local human capital spillover will be summarized to the extent to which the total factor productivity depends on the size and/or significance of γ. dj, dr and dt are industry-fixed effects, region-fixed effects, and year-fixed effects, respectively. In addition to fixed effects, I control for the basic characteristics of plant i, Xijrt , in this case the age of the plant, the type of ownership and the area of the plant’s buildings, which can affect the productivity of the plant.
After taking logs of the production function (1) and substituting for ln Aijrt , (1) can be rewritten as
where yijrt is the log of the value-added amount for the plant. bijrt , wijrt and kijrt are the log of the labor input of white-collar and blue-collar workers and the log capital stock, respectively. One advantage of using repeated cross-sectional data is that doing so allows control over year- and region-fixed effects.10
The main source of endogeneity arises if time-varying region-specific shocks, ϵrt , are positively correlated with the change in the share of college graduates, Hrt . Thus, to address this concern further, I instrument the change in the proportion of college graduates by exploiting the exogenous timing and the size of the positive supply shock in college graduates as induced by the reform. Specifically, during the period analyzed in this paper, the share of college workers in the manufacturing sector increased by a large amount. Figure 5 describes the time trend in the share of college workers proxied by white-collar workers in each region. One can observe an upward trend in most regions after the mid-1980s as well as a certain amount of variation in the increase across the regions. My approach is to use the change in the level of human capital that may be linked to the exogenous educational reform. In particular, I instrument the change in the level of human capital using the freshmen quota prior to the reform, interacted with a dummy variable indicating the periods after the impact of the reform.
Note: The solid blue circles in the figure describe the trend in the proportion of the white-collar workers among all workers in the manufacturing sector in the Mining and Manufacturing Survey.
To be a valid instrument, the instrument should satisfy two conditions. First, it should be correlated with the regional change in the proportion of college graduates among the workforce (the relevance condition). However, it should not be correlated with the unobserved time-varying region-specific shock, which is a source of endogeneity (the exogeneity condition).
My instrument is likely to satisfy the relevance condition if regions with a large initial size of the freshmen quota experience a larger increase in the proportion of college graduates among the workforce after the impact of the reform. This is perhaps due to the mechanical implementation of the policy, which is described in Section II. For instance, if a certain proportion of college graduates obtain jobs where their alma mater is located, a region with a larger initial freshmen quota would experience a larger increase in the share of college graduates among the workforce. The validity of this condition will be tested later by examining the first stage of the 2SLS estimation.
Moreover, the instrument is unlikely to be correlated with a time-varying region-specific shock due to the construction of the instrument. In particular, because the initial freshmen quota was determined prior to the implementation of the reform, it is unlikely that the initial freshmen quota will be correlated with a region-specific shock after the reform. Moreover, the timing of the implementation of the reform did not differ across regions as it was applied to each and every region in 1981. Thus, the interaction term between the two is very unlikely to be related to a time-varying region specific shock.
Using this instrument, which arguably satisfies the two conditions, I use 2SLS to examine the causal effect of, and thus to examine the extent of, the local human capital spillover. Formally, the first stage is as follows:
Here, Hrt denotes the share of college graduates among all workers, as defined earlier in this section. POSTt is a dummy variable that takes a value of one after 1986, when the share of college graduates increased due to the education reform. The relative size of the freshmen quota in 1979 in reference to total employment, PropFresh79rt, is defined as the freshmen quota in 1979 over emprt, the total number of employees in the region, r, at time t. In other words, I instrument the share of college graduates based on the assertion that the initial freshmen quota would have a stronger association with the increase in the number of highly skilled workers after the impact of the policy. This “relevance condition” could be tested by examining the statistical significance of π and the first stage, F-stat.
The second stage of the IV regression uses the predicted value of the proportion of
college graduates from the first stage, 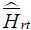 , and estimates with the following equation.
, and estimates with the following equation.
Again, the coefficient of interest is γ . If the instrumental variable is valid, this second stage will address the potential
positive bias associated with simple OLS estimates further, and the estimated coefficient
of 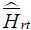 will reveal the regional human capital spillover.
will reveal the regional human capital spillover.
In this section, I provide the estimation results. I begin by documenting the correlation between the proportion of college graduates among workers in a given region and plant productivity. Table 2 provides the regression results for the various specifications that show a correlation. All specifications control for capital stock, labor input by type of worker, the area of the plant building and year-fixed effects. I also control for the log of capital stock per worker in each region, which helps to control for time-varying region-specific productivity shocks. Labor inputs are measured according to the number of employees, and the capital stock is measured as the monetary value of the assets excluding the value of the land. Columns (2) and (4) control for additional characteristics of the plants, such as the age, type of ownership, and industry at the two-digit level. In addition, columns (3)-(4) control for the region-fixed effects. The results in columns (1)-(2) exhibit a positive correlation between the level of human capital and plant productivity; this coincides with cross-sectional results in the U.S. as documented by Rauch (1993) and Moretti (2004c). The coefficient is consistently sizable and statistically significant across specifications. In particular, a percentage point increase in the proportion of white-collar workers in a given region—which is used as a proxy for the share of college graduates—is associated with a 0.75 percent increase in plant productivity.
Columns (3) - (4) show that after controlling for the region-specific fixed effects, the magnitude of the main coefficient decreases, as expected. In particular, the sizes of the coefficients vary from 0.3 to 0.4, which is approximately half of the magnitude of the simple correlation between the level of human capital and productivity. However, the point estimates of the main coefficient in columns (3) and (4) are still somewhat sizable and statistically different from zero. Overall, the results from Table 2 show that a positive correlation between plant productivity and level of human capital exists in Korea. In the remainder of this section, I show that the magnitude of the coefficient decreases as I address the endogeneity further by exploring the implementation of the reform.
Table 3 conveys the results of the IV regression and the corresponding reduced-form result. Columns (1) and (2) report the first stage, and columns (3) and (4) report the second stage. Even-numbered columns additionally control for the individual characteristics of each plant. The first stage of both specifications is strong as the coefficient of the interaction term is statistically significant at the 1% level. Moreover, the F-statistics of the first-stage regression are sufficiently larger than 10. This implies that the instrumental variables are very likely to satisfy the relevance condition. The results from the second stage provide further evidence refuting the existence of human capital spillover, as the magnitude of the main coefficient is smaller than that shown in Table 2. The magnitude of the coefficient from the preferred specification is close to zero, 0.08, and is statistically indistinguishable from zero. In addition to the 2SLS result, columns (5) and (6) report the reduced-form results. Consistent with the 2SLS results, the coefficient of POSTt * PropFresh79rt is close to zero and statistically insignificant. Instrumenting the proportion of college graduates further addresses the endogeneity issue while also correcting the bias in the coefficient of interest. Moreover, the decrease in the magnitude of the coefficient compared to the OLS estimate appears plausible, as the OLS estimate is most likely to be positively biased. Thus, the instrumental variable analysis of this paper provides more compelling estimates. In short, despite a sizable correlation, the effect of the regional human capital level on productivity decreases and becomes statistically insignificant when adopting my instrumental variable, which further corrects the positive bias. Thus, the results provide little support for the existence of human capital spillover beyond plant boundaries in Korea during the 1980s and mid-1990s.
Note: All specifications include the log number of white-collar and blue-collar workers, the log of capital stock and year-fixed effects. Specifications (2) and (4) additionally control for individual plant-specific characteristics such as the industry and the age of the plant. Standard errors in parentheses are clustered at the region-year level. *** p < 0.01, ** p < 0.05, * p < 0.1.
Note: All specifications include the log number of white-collar and blue-collar workers, the log of capital stock and year-fixed effects. Specifications (2), (4) and (6) additionally control for individual plant-specific characteristics such as the industry and the age of the plant. Standard errors in parentheses are clustered at the region-year level. *** p < 0.01, ** p < 0.05, * p < 0.1.
I perform several robustness checks of the IV results. To begin with, I omit intermediate years when the impact of the reform was not fully realized and thus focus on the long-term effects of the policy. In particular, I exclude the years between 1986 and 1993 when the proportion of college graduates in the labor force was increasing steeply as young college graduates were replacing low-skilled workers. Panel A of Table 4 summarizes the estimation result omitting the intermediate years. The estimated effect of regional human capital on productivity is statistically indistinguishable from zero even after omitting the intermediate years.
Note: All specifications include the log number of white-collar and blue-collar workers, the log of capital stock and year-fixed effects. Specifications (2), (4) and (6) additionally control for individual plant-specific characteristics such as the industry and the age of the plant. Standard errors in parentheses are clustered at the region-year level. *** p < 0.01, ** p < 0.05, * p < 0.1.
Furthermore, I check whether the result is robust on different specification for measuring the relationship between human capital and productivity. In particular, I turn to the total factor productivity (TFP) specification, measuring the TFP using the OLS method, after which I examine the whether this measure of productivity depends on the level of human capital in a given region.11 To obtain the TFP measure, I regress the log of the value-added amount of the plant on labor input and on capital and then define the residual of the estimation as the TFP of a plant. The effect of the level of human capital on plant productivity based on the TFP can be summarized as the estimate of λ in the following equation:
Panel B of Table 4 illustrates the results of an instrumental variable analysis using the TFP as an outcome variable. Again, consistent with the main results, the coefficient of the level of region human capital is small and statistically insignificant. Lastly, I use a more general functional form for the production function—a translog specification—instead of the Cobb-Douglas specification and estimate equation (5) including the square of each log input and the interaction between each log input. Panel C in Table 4 reports the results of the instrumental variable analysis under the translog production function. The coefficient of interest is somewhat sizable compared to the main specification but not statistically different from zero. Thus, this analysis shows that the main results are robust with regard to changes in the functional form of the production function.
In this paper, I examine the empirical significance local human capital spillover. In particular, I test whether plants located in regions with higher levels of human capital can produce more with a similar amount of input. To address endogeneity in regional human capital levels, I explore an educational reform in Korea which exogenously changed the level of human capital across regions by increasing existing differences in the supply of college graduates starting in the mid-1980s.
Using this exogenous change, I empirically estimate the relationship between the regional level of human capital and plant productivity. In particular, I explicitly control for endogeneity in the change in the level of human capital using an instrumental variable that utilizes the change in human capital induced by this reform. Overall, I find little evidence supporting the empirical significance of local human capital spillovers in Korea. That is, the productivity of a given plant in a given region is not affected by the level of human capital outside that plant after controlling for the plant’s own human capital and other characteristics.
The results of this paper question the plausibility of human capital spillovers beyond plant boundaries.12 Unlike human capital spillover inside a plant, it is not clear why skilled workers would teach their skills to those less skilled working in other establishments. That is, even if the workers interacted with workers in other plants, human capital spillover beyond plant boundaries is unlikely to occur, as skilled workers have little incentive to pass along their skills without being compensated for doing so.
There could be several other explanations for the relatively small degree of local human capital spillover in Korea. In particular, one may suspect that Korea is too small for the local human capital to exist in the first place. However, as Rosenthal and Strange (2008) document, the extent of the human capital spillover sharply decreases with distances, and most of the externalities stemming from face-to-face interactions are confined within five miles. Thus, it is less likely that the compact size of Korea would be a major factor affecting the small degree of local human capital spillover, as Korea is sufficiently larger than a five-mile radius and thus face-to-face interactions will depend on the location within the country. Other factors can include the long working hours in Korea during the 1980s and 1990s. Specifically, the long working hours in Korea—which often exceeded 2800 hours during the period analyzed in this paper—may have limited the opportunities for workers to interact with workers outside of their plants.
I would like to end this paper by providing several limitations of this work and a related caveat regarding any interpretation of the results. First, this paper does not examine the effects of local human capital spillover separately for each industry with different characteristics, such as the level of technological intensity. This limitation stems from the fact that the dataset does not contain appropriate instrumental variables that can address the endogeneity at the industry-region level. Thus, it is still possible that a specific manufacturing industry may have benefited from the increase in the human capital level of industries with similar characteristics. Furthermore, as human capital in the service sector is not accounted for in the model, this paper does not address the possibility of human capital in the service sector affecting the manufacturing productivity.
Finally, the result of this paper should not be interpreted as evidence that repudiates human capital externalities or human capital spillover in general. Specifically, the results here do not negate all types of human capital spillover. In particular, spillover within a plant where workers are more likely to interact with each other actively may exist. Likewise, human capital externalities that do not depend on physical distances, such as productivity enhancing from R&D, may have been a major source of human capital externalities during the 1980s and 90s in South Korea.
More recently, Niehaus (2012) argues that increased education levels will lead to knowledge spillover by increasing the ability of workers to learn skills from other workers. Alternatively, Acemoglu (1996) proposes that an increase in human capital could have a positive external effect on productivity without involving technology when there is a costly search between workers and firms. This type of human capital externality does not necessarily involve knowledge spillover.
Lange and Topel (2006) and Moretti (2004b) provide a good summary of the literature which uses wage data to document the social returns of education.
The government determined not only the freshmen quota but also the admission guidelines for both private and public colleges.
The government allowed only a small number of disadvantaged students to be accepted over the fresh- men quota. Further, the government provided an incentive for colleges to keep the actual enrollment lower than the freshmen quota. For instance, the government increased the subsidy for colleges if the actual enrollment for a given college was lower than the freshmen quota set by the government.
President Park Chung-hee, who was in office for more than 15 years, was assassinated by his body guard on October 26, 1979. After the assassination, the military junta lead by General Chun Doo-hwan gained control after a series of coups. Many people hoped a democratic government would be established after the assassination, and, as a result, this military junta was not popular. To gain popularity, the junta announced the education reform on July 30, 1980.
Other components included prohibiting private tutoring and abolishing college-specific entrance exams.
Unfortunately, the data do not have location identifier for the establishment, thus I cannot use these data for the main analysis.
The value-added amount for each plant is defined as the value of its output less the cost of production, which includes the costs of materials and electricity.
The survey does contain the plant ID. Unfortunately, the ID is not assigned consistently across years; thus, one cannot control for plant-fixed effects.
Because the data does not contains plant identifiers, I cannot use the methodology proposed by Olley and Pakes (1996) or Levinsohn and Petrin (2003), which controls for endogeneity in the labor and capital input more explicitly.
It is important to note that this paper does not provide evidence that contradicts all types of human capital spillover. For instance, human capital spillover inside a plant or peer effects where workers are more likely to interact may still exist (Mas and Moretti 2009).
(1996). A Microfoundation for Social Increasing Returns in Human Capital Accumulation. The Quarterly Journal of Economics, 111(3), 779-804, https://doi.org/10.2307/2946672.
(1962). The Economic Implications of Learning by Doing. The Review of Economic Studies, 29(3), 155-173, https://doi.org/10.2307/2295952.
(1996). The Impact of Shifts in Supply of College Graduates: Repercussion of Educational Reform in Korea. Economics of Education Review, 15(1), 1-9, https://doi.org/10.1016/0272-7757(95)00031-3.
, & (2006). Identifying Human-capital Externalities: Theory with Applications. Review of Economic Studies, 73(2), 381-412, https://doi.org/10.1111/j.1467-937X.2006.00380.x.
, & (2001). Schooling Data, Technological Diffusion, and the Neoclassical Model. American Economic Review, 91(2), 323-327, https://doi.org/10.1257/aer.91.2.323.
, , & (2010). Identifying Agglomeration Spillovers: Evidence from Winners and Losers of Large Plant Openings. Journal of Political Economy, 118(3), 536-598, https://doi.org/10.1086/653714.
, & (1999). Why Do Some Countries Produce So Much More Output per Worker than Others? The Quarterly Journal of Economics, 114(1), 83-116, https://doi.org/10.1162/003355399555954.
(2012). Do Clusters Really Matter for Innovation Practices in Information Technology? Questioning the Significance of Technological Knowledge Spillovers. Journal of Economic Geography, 12(1), 107-126, https://doi.org/10.1093/jeg/lbq058.
, & (2009). Schooling Externalities, Technology, and Productivity: Theory and Evidence from U.S. States. The Review of Economics and Statistics, 91(2), 420-431, https://doi.org/10.1162/rest.91.2.420.
, & (2003). Estimating Production Functions Using Inputs to Control for Unobservables. The Review of Economic Studies, 70(2), 317-341, https://doi.org/10.1111/1467-937X.00246.
(1988). On the Mechanics of Economic Development. Journal of Monetary Economics, 22(1), 3-42, https://doi.org/10.1016/0304-3932(88)90168-7.
(1993). Making a Miracle. Econometrica, 61(2), 251-272, https://doi.org/10.2307/2951551.
, & (2009). Peers at Work. American Economic Review, 99(1), 112-145, https://doi.org/10.1257/aer.99.1.112.
(2004a). Estimating the Social Return to Higher Education: Evidence from Longitudinal and Repeated Cross-sectional Data. Journal of Econometrics, 121(1-2), 175-212, https://doi.org/10.1016/j.jeconom.2003.10.015.
(2004c). Workers’ Education, Spillovers, and Productivity: Evidence from Plantlevel Production Functions. American Economic Review, 94(3), 656-690, https://doi.org/10.1257/0002828041464623.
, & (1996, November). The Dynamics of Productivity in the Telecommunications Equipment Industry. Econometrica, 64(6), 1263-1297, https://doi.org/10.2307/2171831.
(1993). Productivity Gains from Geographic Concentration of Human Capital: Evidence from the Cities. Journal of Urban Economics, 34(3), 380-400, https://doi.org/10.1006/juec.1993.1042.
(1986). Increasing Returns and Long-run Growth. Journal of Political Economy, 94(5), 1002-1037, https://doi.org/10.1086/261420.
, & (2008). The Attenuation of Human Capital Spillovers. Journal of Urban Economics, 64(2), 373-389, https://doi.org/10.1016/j.jue.2008.02.006.