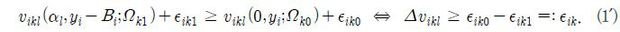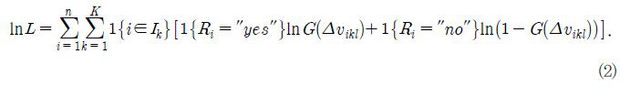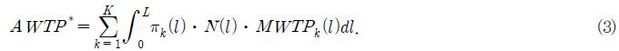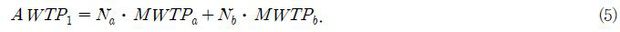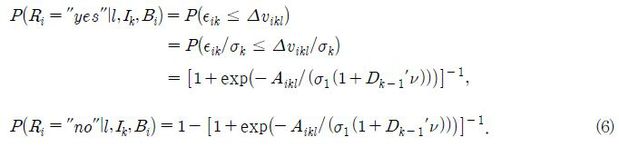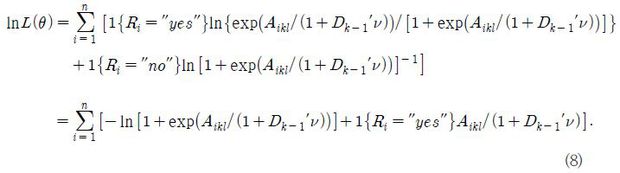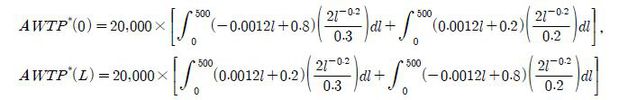Calculation of Total Benefit by the Contingent Valuation Method for Cost-Benefit Analysis: Focusing on Income and Distance-Decay Effects
Abstract
This study suggests a model for calculating total benefit rigorously to use the contingent valuation method (CVM) in cost-benefit analysis (CBA). Estimating households’ willingness to pay through survey method, the study attempts to demonstrate if a respondent’s income and the distance between a respondent’s residence and the location of a target facility affect her willingness to pay. The estimation results from a structural model show that income and distance-decay effects exist and that the calculated total benefit varies largely when these effects are ignored.
The study emphasizes the effects of income and distance-decay on the total benefit must be carefully considered in using CVM for CBA. Even though the total project cost is precisely estimated, the benefit/cost (B/C) ratio may differ largely when the total benefit is not correctly calculated. Also, an ad hoc model generates significantly different estimates from the utility difference model this study adopted. The difference in estimates suggests that the total benefit has to be estimated by a structural model.
Finally, simulations are performed to check the validity of the model as well as to predict consequences when income and distance-decay effects are not properly treated. The results from simulations reveal it is not desirable to ignore those effects considering the perspectives of balanced regional development.
Keywords
조건부가치측정법, 지불의사액, 소득효과, 거리-소멸 효과, Contingent Valuation Method: CVM, Willingness to Pay: WTP, Income Effect, Distance-Decay Effect
JEL Code
C54, H54, Q57, R53
Ⅰ. 서 론
조건부가치측정법(contingent valuation method, 이하 CVM)은 환경재 등 시장이 형성되지 않은 재화의 비사용가치(non-use value)를 측정하는 방법으로 널리 쓰여왔다(CVM의 성과와 적용에 대한 종합적인 개괄은 Smith[2006]를 참조). 또한 CVM을 응용하면 신제품의 출시 또는 새로운 시설물의 설치를 결정하기 위한 비용편익분석(cost-benefit analysis)에도 이용 가능하다. 실제로 CVM은 시행을 고려하고 있는 공공사업의 편익산정을 위해 널리 이용되어 왔다(한국개발연구원[2008]).
CVM은 현재 대상 재화가 시장에서 거래되지 않기 때문에 소비자의 진술선호(stated preference)를 도출하기 위해 설문을 통해 지불의사(willingness to pay: WTP) 금액을 구하는 방법을 사용한다. 공공사업의 비용편익분석을 위해서는 도출된 가구당 지불의사액을 합산하여 해당 시설이 제공하는 총편익을 산정하고, 조성비용(총사업비)과의 비교를 통해 사업의 추진 여부를 정하는 의사결정의 근거로 삼는다. 이때 합산방식에 따라 총편익의 크기가 달라질 수 있기 때문에 지불의사액의 합산(aggregation)의 문제는 비용편익분석에 있어 매우 중요한 요소가 된다.
총편익 산정의 가장 단순한 방법으로는 모든 표본에 대한 가구당 평균지불의사액을 구한 뒤 여기에 단순히 총 가구 수를 곱하여 총지불의사액을 구하는 방식이 있다. 한 걸음 나아가 우리나라의 경우 해당 공공시설이 위치한 광역시⋅도를 ‘인접지역’으로, 그 외의 지역 모두를 ‘비인접지역’으로 나누어 두 개의 가구당 평균지불의사액을 도출한 뒤, 이의 각각에 해당하는 총 가구 수를 곱한 뒤 이 둘을 합하는 방식으로 총지불의사액을 구하는 방식을 채택하는 경우도 있다(한국개발연구원[2008] 등 참조).
본 연구는 지불의사액의 합산에 있어, 보다 엄밀한 산정방식을 도입하여 기존의 방식과 비교⋅분석함으로써 연구자들이 CVM을 비용편익분석에 적용함에 있어 유의해야 할점을 밝히고자 한다. 대부분의 CVM 연구에서 응답자의 사회경제적 특징(socio-economic characteristics)은 WTP 추정치의 통계적 유의성을 확인하는 정도의 보조적인 정보로만 사용되는 경우가 많은데, 본 연구에서는 응답자의 소득 및 응답자의 거주지와 공공시설까지의 거리에 따라 지불의사액이 달라질 수 있음에 착안하여 이들을 모형화하고 보다 정확한 총편익 산정방법을 제시하고자 한다.
먼저 응답자의 소득이 지불의사액의 크기에 영향을 준다는 연구는 활발히 진행되어 왔다(Eckerlund et al.[1995]; Horowitz and McConnell[2003] 등 참조, 소득효과에 대한 메타분석은 Schläpfer[2006]를 참조). 즉, 특정 제시금액에 대해 소득이 높은 응답자의 경우, 낮은 소득을 얻는 응답자보다 상대적으로 높은 지불의사를 가지는 경향이 있다. 이는 제시금액을 소득에서 제하더라도 전체 소득에 미치는 영향이 상대적으로 작음에 기인한다. 응답자의 소득정보를 얻는 방식에 있어서, 응답자 자신도 본인의 정확한 소득을 알지 못하는 경우 또는 소득이 일정 범위 내에서 자주 변화하는 경우 등 소득을 정확히 관측하는 것은 현실적으로 매우 어렵기 때문에 흔히 구간을 제시하고 응답자가 본인이 해당하는 소득구간을 선택하도록 하는 방법으로 설문지를 설정한다.
한편, 공공시설의 입지와 응답자의 거주지 간의 거리에 따라 해당 공공시설이 제공하는 편익이 달라질 수 있다. 공공시설과 거주지 간의 거리가 멀어질수록 여행비용 또는 방문에 소요되는 시간이 증가하기 때문에 응답자가 공공시설을 방문하는 빈도가 낮아질 수 있고 이에 따라 편익의 크기가 줄어들 수 있다. 이를 고려하기 위해 기존 연구들은 ‘거리-소멸 함수(distance-decay function)’를 상정하여 거리의 영향을 측정하는 다양한 시도를 해왔다(Pate and Loomis[1997]; Hanley et al.[2003]; Bateman et al.[2006]; Concu[2007]; 엄영숙[2010] 등).
본 연구는 편익에 영향을 미치는 이들 두 요소(소득과 거리)를 고려하여 추정된 응답자의 지불의사액을 합산하여 산정된 총편익과, 기존에 흔히 사용된 단순합계방식을 비교하고자 한다. 이때 앞서의 논의와 같이 소득의 구간자료의 특성 및 편익의 거리-소멸 효과를 모형에 내재화(internalize)하여 구조적인 추정(structural estimation)을 수행하는 것을 목적으로 한다. 그리고 모집단의 경험분포(empirical distribution)를 이용하여 총편익을 산정함으로써 보다 정확한 값을 도출하고자 한다. 따라서 본 연구의 가장 큰 기여는 기존에 소득효과 또는 거리-소멸 효과만을 고려한 연구들과 달리 소득과 거리 모두를 고려한 구조모형(structural model)을 제시한다는 점이다. 기존 연구 중 Bateman et al.(2000)이 소득효과와 거리-소멸 효과를 모두 고려한 사례가 있으나, 해당 연구는 WTP를 종속변수로 하고 소득과 거리를 독립변수로 하는 임의적인 축약모형(reduced-form model)을 이용한 것으로 이론적 근거가 미약하다고 할 수 있다.
소득효과의 경우 주목할 만한 대표적 기존 연구로 McFadden and Leonard(1993)의 연구를 들 수 있는데, 이들은 효용함수 내에 소득에 대한 민감도를 모수로 두어 추정하는 방식을 채택함으로써 소득효과를 구조모형으로 추정하였다. 본 연구는 이와 같이 모든 표본에 대해 단일 모수로 소득에 대한 민감도를 고려하는 대신 표본 내 소득그룹별로 상이한 민감도를 추정한다는 점에서 차별성을 지닌다. Diamond et al.(1993, p.42)이 지적한 바와 같이 일반적으로 WTP에 대한 한계소득효과는 소득이 증가할수록 체감하는 경향을 보이는데, 본 연구의 방식을 통해 이와 같은 비선형적인 소득효과를 설명할 수 있다는 점에서 기존 연구보다 일반적인 방식이라 할 수 있다.
한편, 거리-소멸 효과와 관련하여 본 연구의 기여는 먼저 기존의 Hanley et al.(2003) 및 Bateman et al.(2006) 등과 같이 WTP를 종속변수로 하고 거리를 독립변수로 하는 축약모형을 이용한 방식과 달리 구조모형을 이용한다는 점에서 임의적인 축약 모형의 선택을 배제하였다는 점이다. Concu(2007)는 확률효용모형(random utility model)하에서 공간적 이질성(spatial heterogeneity)을 고려한 구조모형을 제시한 점에서 거리-소멸 효과를 다루는 관점이 본 연구와 가장 유사한 형태를 보인다. 그러나 해당 연구는 대상 재화의 몇 가지 일반적 특징(generic characteristics)에 대한 공간적 이질성을 가정하였으나 본 연구는 재화의 특징과 무관하게 응답자의 거주지와 대상 재화간의 거리에 의한 공간적 이질성만을 고려한다는 점이 상이하다.
한편, 본 연구가 상정하는 소득과 거리의 두 요소 이외에 CVM 설문을 통해 얻어진 응답자의 기타 사회경제적 특징(교육수준, 성별, 나이, 환경단체 가입 여부 등) 또한 WTP에 영향을 주는 요소로 생각할 수 있을 것이다. 그리고 이들을 고려한다면 이들이 주어진 상황에서 WTP 추정치의 통계적 효율성이 높아질 수도 있을 것이다. 그러나 이들은 다음과 같은 이유로 모형에 내재화하지 않았다. 첫째, 소득 및 거리에 대한 WTP의 주변분포(marginal distribution)를 이용하는 것이 여타 변수들의 조건부 모멘트(conditional moment)에 대한 가정을 하지 않음으로써 보다 단순하고 통계적으로 정당한 방식이라고 할 수 있다(McFadden and Leonard[1993], pp.186~187). 둘째, 해당 요소에 대한 모집단의 정확한 분포를 알기 어렵다. 예컨대 환경단체 가입자의 세부지역별 분포와 같은 정보는 현실적으로 정확히 구하기 어렵기 때문에 오히려 총편익의 산정에 오차로 작용할 여지가 있다. 따라서 이와 같은 요소들은 현재 널리 사용되는 방식과 같이 WTP 추정치의 신뢰도를 검증하는 보조적인 도구로 사용하는 것이 바람직할 것이다. 다만, WTP에 크게 영향을 주는 요소가 있는 특수한 상황에서, 필요한 경우 기타 요소에 대해 본 연구의 방법을 적용할 수 있다. 예컨대 입자가속기와 같은 연구시설의 건립시 교육수준이 높으면 WTP가 높을 것이라고 연구자가 확신하고, 세부지역별 교육수준에 대한 모집단의 분포를 잘 알고 있는 경우를 들 수 있다. 앞서 설명한 바와 같이 본 연구는 구간자료(소득)와 연속자료(거리)의 처리방식을 모두 논하고자 하므로 기타 요소에 해당하는 변수의 특성에 맞추어 해당 방식의 적용이 가능할 것이다. 즉, 교육수준을 모형에 내재화하고자 하며 교육수준이 구간자료로 얻어진 경우라면 본 연구에서 소득을 처리한 방식을 사용할 수 있다.
이하 본 연구의 구성은 다음과 같다. 제Ⅱ장에서는 CVM에서 지불의사액이 응답자의 소득 및 응답자의 거주지와 해당 공공시설 사업지 간의 거리에 따라 달라지는 효과를 고려한 분석모형을 설정하고, 이에 따른 총편익의 산정을 기존 방식과 비교하였다. 그리고 제Ⅲ장에서는 설정된 모형을 추정하는 방법을 제시하였다. 제Ⅳ장에서는 실제 사례에 모형을 적용하여 총편익을 산정한 결과와 논의를 담았으며, 제Ⅴ장에서는 시뮬레이션을 통해 모형의 적합성을 검증하고 모형의 선택에 따른 총편익 산정에서의 함의를 살펴본다. 마지막으로 제Ⅵ장은 결론 및 정책제언에 할애하였다.
Ⅱ. 분석모형
1. 설문 디자인
먼저 응답자의 단위는 가구(household)이며, 비용편익분석의 대상이 되는 재화는 공공사업을 통한 시설물이라 하자.1 각 가구가 공공시설의 건립을 위해 지불할 용의가 있는 금액은 설문을 통해 얻는다. 이때 현실에서 소비자가 흔히 구매를 결정하는 상황과 근접한 방식을 채택함으로써 여러 가지 편의(bias)를 최소화하기 위해 추천되는 방식은 응답자가 해당 공공시설을 실제로 사용하든 안하든 이 시설이 건립되는 대신 제시된 특정 금액만큼을 소득에서 포기할 용의가 있는지의 여부(‘예/아니오’)를 묻는 양분선택(dichotomous choice: DC) 모형이다(Arrow et al.[1993]).2 이와 같은 질문을 한 번 함으로써 지불의사액 구간의 정보를 얻는 모형을 단일경계 양분선택(single-bounded dichotomous choice: SBDC) 모형이라 한다. 한편, 이중경계 양분선택(double-bounded dichotomous choice: DBDC) 모형은 첫 제시금액에 대한 지불용의 여부에 따라 보다 높은 금액(‘예’의 경우) 또는 보다 낮은 금액(‘아니오’의 경우)을 한 번 더 물어봄으로써 구간의 크기를 좁혀 추가적인 정보를 얻는 방식이다. 이들 모형 간의 선택에 관한 논의는 많이 있어 왔는데, 본 연구에서는 논의의 초점을 구조적인 추정에 맞추기 위해 SBDC 모형을 채택하기로 한다.3
CVM 설문상의 추가적인 유의점은 먼저 응답자가 해당 공공시설 및 대체재에 대해 충분히 인지할 수 있는 정보를 제공해야 한다는 점과, 지불의사액을 도출함과 더불어 응답자의 사회경제적 특성에 대한 정보도 충분히 취합해야 한다는 점을 들 수 있다. 본 연구에서는 응답자의 거주지 정보를 취득함으로써 대상 공공시설과의 거리를 알 수 있고, 응답자의 소득에 대한 구간정보를 얻을 수 있도록 디자인된 설문지를 상정한다.
2. 지불의사액 도출4
각각의 가구 i는 어떤 소득집단 Ik에 속하며(k = 1,…, K), 향후 건립을 고려하고 있는 공공시설과 l만큼의 거리에 떨어져 거주하고 있다. 해당 거리와 소득집단의 가구는 간접효용함수 Uikl(αl, yi; Ωkj)을 가진다. 이때 αl은 어떤 공공시설이 l만큼의 거리에 떨어져 거주하는 가구에 제공하는 편익의 크기이다. 한편, yi는 해당 가구의 소득, Ωkj는 상황 j∈{0, 1}의 발생이 예상되었을 때 소득집단 Ik에 주어지는 정보집합(information set)을 의미한다. 즉, Ωkj는 소득집단 Ik에 속하는 가구가 선택을 하는 데 있어 필요한 모든 정보를 담고 있다.
공공시설의 건립을 상황 1, 그렇지 않은 경우를 상황 0이라 할 때, 가구 i에 공공시설 건립을 위해 Bi만큼의 금액을 지불할 용의가 있는지를 묻는다면 다음과 같은 경우 “그렇다”는 응답을 할 것이다.
즉, 공공시설의 건립을 위해 Bi만큼의 금액을 지불하는 대신, 건립을 통해 αl만큼의 추가적인 편익을 얻게 되는 상황에서 소비자는 공공시설이 건립되는 상황이 가져다주는 효용이 그렇지 않은 경우보다 클 경우 Bi의 금액을 지불할 용의가 있게 되는 것이다. 이때 간접효용함수를 연구자의 관점에서 관측 가능한 부분(vikl(αl, yi; Ωkj))과 관측 불가능한 부분(ϵikj) 간에 가산적으로 분리 가능(additively separable)하다고 가정하여, 다음과 같이 표현할 수 있다고 하자. υ
그러면 위 식 (1)은 다시 다음과 같이 표현된다.
이때 관측 가능한 효용격차는 Δvikl := vikl(αl, yi − Bi;Ωk1) − vikl(0, yi;Ωk0)이며, 관측 불가능한 효용격차 ϵik는 평균이 0이고 분산이  인 확률분포 G를 따른다고 가정한다.
인 확률분포 G를 따른다고 가정한다.
CVM의 DC 설문은 특정한 금액을 제시하고 이를 지불할 의사가 있는지 없는지를 물어봄으로써, 현실적으로 응답자 스스로 지불의사액의 정확한 금액을 도출하는 것이 매우 어렵다는 문제를 완화하고자 한다. 따라서 응답자가 Bi의 제시금액에 지불의사를 표시했다면 위 식 (1′)에서 등호를 만족하는 경우뿐만 아니라 부등호에 해당하는 경우를 포함하므로 응답에 의한 정보는 반개구간(half-open interval)으로 얻어진다. 이는 동일한 제시금액에 대해 지불의사가 없음을 표시한 경우에도 마찬가지이다. 따라서 응답자 i가 제시금액 Bi에 대해 표시한 지불의사(‘예/아니오’)를 Ri라 할 때 ‘예’의 응답을 할 확률은 P(Ri = ″yes″) = G(Δvikl)이다. 그렇다면 n개의 표본을 얻은 뒤 다음의 로그우도함수(log-likelihood function)를 이용한 최우추정법(maximum likelihood estimation: MLE)을 이용하여 지불의사액의 모수를 추정할 수 있다.
이때 1{•}는 괄호 안의 내용이 참이면 1, 그렇지 않으면 0의 값을 가지는 지시함수(indicator function)이다.
여기서 본고가 중점적으로 확인할 사항은 응답자의 소득 및 응답자의 거주지와 대상지까지의 거리가 지불의사액에 영향을 미치는가 하는 점이다. 먼저 소득의 경우 많은 기존 연구에서 소득이 높을수록 지불의사액이 커짐을 이론 및 실증적으로 보여주고 있다. 따라서 추정 시 각 소득구간 Ik에 상응하는 모수의 크기가 달라지도록 허용함으로써 이와 같은 소득효과를 설명하고자 한다. 한편, 응답자의 거주지와 대상지까지의 거리 정보를 이용하여 지불의사액에 미치는 거리-소멸 효과를 확인하고자 한다. 이는 모형의 αl을 모수화(parametrization)함으로써 얻을 수 있다. 상세한 모수화와 추정방법은 제Ⅲ장에서 다루기로 하고, 본 장에서는 총편익 산정방식을 비교하기로 한다.
3. 총편익의 산정
먼저 각각의 소득집단 Ik에 대해 주어진 거리 l에 해당하는 가구당 평균지불의사액을 MWTPk(l)이라 할 때 총편익은 다음과 같다.
이때 πk(l)은 특정 거리 l에 해당하는 소득집단 Ik의 경험확률밀도(empirical probability density)이며, N(l)은 거리 l에서의 모집단의 가구 수이다. 따라서 πk(l) • N(l)은 특정 거리 l의 총 가구 수 중 소득집단 Ik에 해당하는 가구 수를 나타낸다. 한편, L은 총편익을 산정할 때 고려하는 모집단 중 공공시설과 가장 멀리 떨어져 있는 소비자 가구와 공공시설 간의 거리를 나타낸다.
반면, 소득과 거리를 고려하지 않은 모형을 통해 산정되는 총편익은 다음과 같다.
즉, 모든 표본에 대한 가구당 평균지불의사액 MWTP0를 구한 뒤 여기에 모집단의 가구 수 N을 곱하여 총편익 AWTP0을 산정한다. 이와 같은 방식의 문제점은 응답자의 가구소득 및 응답자의 거주지와 공공시설 간의 거리가 모두 반영되지 않은 가구당 평균지불의사액 MWTP0이 대표성을 갖고 있지 않음에 있다.
만일 총편익의 산정에 있어 거리의 영향을 불완전하게나마 고려하기 위해 응답자 가구의 거주지를 바탕으로 표본을 인접지역(a) 및 그보다 멀리 떨어진 기타 지역(b)의 두 가지로 구분한다면 총편익은 다음과 같이 표현된다.
즉, 먼저 인접지역의 표본만을 대상으로 가구당 평균지불의사액 MWTPa를 구하고 여기에 인접지역의 가구 수 Na를 곱하여 인접지역의 총편익을 산정한다. 같은 방식으로 기타 지역의 가구당 평균지불의사액 MWTPb와 가구 수 Nb로부터 기타 지역의 총편익을 얻은 뒤 이들을 합하여 전국의 총편익 AWTP1을 구하는 방식이다. 이와 같은 방법 역시 MWTPa와 MWTPb의 대표성이 문제가 되며, 거리-소멸 효과가 존재하는 상황에서 행정구역 단위에 맞추어 임의로 표본을 나누는 문제도 있다. 예컨대 부산, 울산 및 경상남도를 인접지역으로 묶었을 때 경상남도 내 어떤 지역 1의 거리가 경상북도 내 특정 지역 2의 거리보다도 먼 경우가 있음에도 불구하고 해당 방식은 지역 1은 인접 지역으로, 지역 2는 기타 지역으로 구분함으로써 편의를 야기하는 문제가 있다. 보다 심각한 문제는 근본적으로 표본을 둘로 나누어 각각의 평균지불의사액을 따로 구하는 방법이므로 각 지역의 표본 수가 현저히 줄어들어 정보의 손실이 크다는 점이다.
마지막으로 제시금액 Bi에 대해 지불의사가 없다는 응답 중에는 단순히 지불의사가 없다고 해석되기보다는 설문 자체에 대한 응답을 거부한 ‘응답 거부(protest response)’ 도 포함되어 있기 때문에 NOAA 패널의 지침(Arrow et al.[1993])이 권고하듯이 이들은 표본에서 제외하고 분석하는 것이 바람직하다.5 엄영숙(2010)은 총편익 산정 시 이를 고려하여 표본 중 각 거리별 응답 거부의 비율만큼을 모집단의 가구 수에서 제외하는 방식을 사용하였다. 이와 같은 방식을 식 (3), (4) 및 (5)에 적용할 수 있으나, 본 연구에서는 다음과 같은 이유로 총편익 산정 시 응답 거부 비율을 고려하지 않는다. 첫째, 총편익 산정에 있어 응답 거부 비율을 사용하는 것은 기본적으로 응답 거부에 대해 MWTPk(l) ≡ 0을 가정하는 것이다. 이는 응답 거부가 설문 자체에 대한 응답을 거부한 것이며, 지불의사가 없음을 의미하는 것은 아니라는 점에서 옳지 못한 가정이다. 둘째, 응답 거부의 경우 MWTPk(l) ≃ 0일 것이라는 가정을 받아들인다 해도, 표본 개수의 제약으로 인해 식 (3)의 경우 특정 소득구간과 거리에 해당하는 응답자의 수가 매우 제한적이므로 얻어진 응답 거부 비율이 대표성을 가진다고 보기 어렵다. 따라서 산정된 총편익에 응답 거부 비율을 적용하는 것은 추가적인 오차를 발생시킬 수 있다. 셋째, 소득효과 및 거리-소멸 효과를 고려하는 모형과 이들을 고려하지 않고 흔히 사용되는 경우를 엄밀히 비교하고자 하는 본 연구의 목적상 응답 거부를 고려하지 않고자 한다. 이는 대부분의 연구 및 비용편익분석에서 식 (4) 또는 식 (5)의 방식을 취하고 있기 때문이다.
Ⅲ. 효용격차모형의 추정
추정을 위해 소득집단 Ik에 속하는 응답자 i의 관측되지 않는 효용격차 ϵik의 분포는 독립적으로 평균이 0이고 분산이  인 로지스틱 분포를 따른다고 하자. 이와 같이 소득집단들의 분산에 존재할 수 있는 이질성(heterogeneity)을 고려하기 위해 최저 소득집단(k = 1)을 기준으로 하는 ((K − 1) × 1) 더미변수 벡터 Dk-1을 상정하자. 그러면 소득집단 Ik의 표준편차는 (k − 1)번째 요소(component)에만 1을 갖는 Dk-1하에서 ν := (ν2, ν3, … , νK)일 때 σk = σ1(1 + Dk-1′ν)와 같다(Kunimitsu[2006], p.36 참조). 이때 k > 1인 경우 소득집단 Ik가 최저 소득집단과 상이한 분산을 가진다면 해당 νk의 추정치는 통계적으로 유의하게 0과 다른 값을 가질 것이다. 그렇다면 ‘예/아니오’의 응답확률은 각각 다음과 같이 구해진다.
인 로지스틱 분포를 따른다고 하자. 이와 같이 소득집단들의 분산에 존재할 수 있는 이질성(heterogeneity)을 고려하기 위해 최저 소득집단(k = 1)을 기준으로 하는 ((K − 1) × 1) 더미변수 벡터 Dk-1을 상정하자. 그러면 소득집단 Ik의 표준편차는 (k − 1)번째 요소(component)에만 1을 갖는 Dk-1하에서 ν := (ν2, ν3, … , νK)일 때 σk = σ1(1 + Dk-1′ν)와 같다(Kunimitsu[2006], p.36 참조). 이때 k > 1인 경우 소득집단 Ik가 최저 소득집단과 상이한 분산을 가진다면 해당 νk의 추정치는 통계적으로 유의하게 0과 다른 값을 가질 것이다. 그렇다면 ‘예/아니오’의 응답확률은 각각 다음과 같이 구해진다.
위 식 (6)에서 기본적으로 Δvikl ≡ Aikl이나, Aikl은 벡터표기방식에 의한 스칼라(scalar)를 나타낸다.
추정을 위해 거리에 따른 편익과 소득에 의한 효용이 가산적으로 분리 가능하다고 가정하고, 소득에 대해 선형의 간접효용함수 형태를 가정하였다. 즉, 응답자 i가 제시금액 Bi만큼을 지불하고 얻는 관측 가능한 효용은 다음과 같다.
이때 관측 가능한 효용격차 Δvikl = αl − βkBi가 제시금액 Bi에 대해 선형의 함수 형태를 가짐을 알 수 있다. 그리고 로지스틱 분포의 대칭성을 이용하면 가구당 평균지불의사액의 추정치  은
은 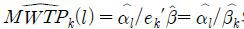 와 같이 얻어진다(Hanemann [1984], p.335). 이때 ek는 k번째 요소에만 1을 가지고 나머지는 모두 0인 (K × 1)벡터이며, β = (β1, … , βK)이다.
와 같이 얻어진다(Hanemann [1984], p.335). 이때 ek는 k번째 요소에만 1을 가지고 나머지는 모두 0인 (K × 1)벡터이며, β = (β1, … , βK)이다.
한편, 소득에 대한 한계효용이 체감하는 간접효용함수의 한 형태로서 소득의 로그값에 대해 선형인 간접효용함수를 상정한다면 효용격차는 다음과 같이 표현된다.
이때 소득 대비 제시금액의 비율 Bi/yi가 매우 작으므로, 위와 같은 근사식을 이용할 수 있다. 그렇다면 해당 소득집단의 평균소득 yk를 이용하여 Aikl = αl − ek′β(Bi/yk)를 얻을 수 있고, 이때 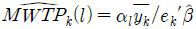 로 얻어지므로 효용격차 및 MWTP 모두 소득의 영향을 받게 되지만, 그 추정치는 앞서 구해진 값과 동일함을 알 수 있다. 즉, 소득에 대해 한계효용이
체감하는 간접효용함수라도 소득 대비 제시금액이 매우 작기 때문에 식 (7)과 같이 선형의 간접효용함수로 근사됨을 알 수 있다.
로 얻어지므로 효용격차 및 MWTP 모두 소득의 영향을 받게 되지만, 그 추정치는 앞서 구해진 값과 동일함을 알 수 있다. 즉, 소득에 대해 한계효용이
체감하는 간접효용함수라도 소득 대비 제시금액이 매우 작기 때문에 식 (7)과 같이 선형의 간접효용함수로 근사됨을 알 수 있다.
또한 비교를 위해 관측 가능한 효용격차가 로그를 취한 제시금액 ln Bi에 대해 선형의 형태를 가지는 경우를 상정하였다. 이때 역시 소득에 대해 한계효용은 체감하나, 제시금액을 지불하는 경우 소득상의 영향은 lnyi − lnBi와 같이 나타남을 알 수 있다. 이는 앞서 설정한 효용격차 구조모형을 따르지 않지만 유사한 형태의 임의적인 모형설정 오류(model misspecification)를 부여한 경우 추정 결과에 어떤 영향을 미치는지를 비교⋅확인하고자 한 것이다.
거리에 따른 편익의 크기 αl은 <Table 1>에서 보는 바와 같이 세 가지 함수 형태를 가정하였다. 먼저 거리에 따른 선형함수(모형 Ⅰ)와 거리의 멱함수(power function)를 가정하여(모형 Ⅱ) 추정에 사용하였다. 마지막으로 펼쳐진 지수함수(stretched exponential function)를 도입하여(모형 Ⅲ) αl이 거리에 따라 변화하는 행태를 유연한(flexible) 함수 형태로 표현하여 앞서의 선형함수 및 멱함수와 비교하고자 한다. 펼쳐진 지수함수는 소멸효과를 설명하는 데 흔히 사용되는 함수의 형태로서, <Table 1>에서 설정된 형태의 경우 γ1 > 0이고 γ2 < 0인 경우에 αl은 l의 단조감소함수가 된다. 그리고 γ3 = 1인 경우에는 일반적인 지수함수가 되며, γ3 = 2일 때 적절한 (γ0, γ1, γ2)의 값이 주어지면 정규분포의 확률밀도함수가 된다. 이와 같이 펼쳐진 지수함수는 모수의 값에 따라 그 모양이 다양하게 바뀌는 매우 유연한 함수로서 모형 Ⅰ과 Ⅱ의 가정이 타당한지를 확인할 수 있는 척도가 될 것이다.
모형 Ⅰ과 Ⅱ에 대해 γ1 < 0인 경우, 그리고 앞서 설명한 바와 같이 모형 Ⅲ에서 γ1 > 0이고 γ2 < 0인 경우에 αl은 l의 단조감소함수이며, 이는 총편익 산정과 관련한 기존 문헌에서 거리의 영향을 고려하기 위해 흔히 상정하는 단조적인 거리-소멸 함수이다(단조함수가 아닌 거리의 영향을 고려한 공간적(spatial) 연구는 Johnston et al.[2011] 등을 참조). 다른 조건이 모두 같을 경우, 여행비용이나 접근성에 의한 불편비용 등에 의해 거리에 따른 편익의 크기 αl은 일반적으로 l의 감소함수(decreasing function)로 생각할 수 있으나, l이 매우 작은 경우에는 소음 또는 교통체증 등의 불편함 때문에 오히려 l의 증가함수일 수도 있을 것이다.6 그러나 전국을 대상으로 하는 총편익 산정의 경우에 있어 αl을 l의 단조함수(monotone function)로 보고 위와 같이 가정한다. 모든 모형에 대해 γ1 = 0은 응답자의 거주지와 공공시설 간의 거리가 응답자의 편익에 영향을 주지 않는 경우이다.
한편, 모든 모형에서 γ1 , β와 σ1을 분리하여 식별(identification)할 수 없으므로 σ1 =  ≡ 1로 정규화(normalization)한다. 이제 위 식 (6)을 로그우도함수 (2)에 대입하여 모수 θ = (γ, β, ν)를 추정할 수 있다. 추정에 사용된 로그우도함수는 다음과 같다.
≡ 1로 정규화(normalization)한다. 이제 위 식 (6)을 로그우도함수 (2)에 대입하여 모수 θ = (γ, β, ν)를 추정할 수 있다. 추정에 사용된 로그우도함수는 다음과 같다.
<Table 2>에서는 추정에 사용된 여섯 가지 모형을 비교하여 나열하였다. 이때 최우측열에 있는 가구당 평균지불의사액 추정치를 식 (3)의 MWTPk(l)에 대입하면 각각의 모형에 대해 소득과 거리를 고려한 총편익의 추정치 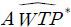 를 구할 수 있다.
를 구할 수 있다.
이때 <Table 2>에서 구해진 가구당 평균지불의사액을 통해 식 (3), (4) 및 (5)의 총편익 산정방법을 살펴보면, 모든 모형에서 γ1 = 0이고 β1 = β2 =…= βK인 경우에만 AWTP* = AWTP0 = AWTP1임을 알 수 있다. 비교를 위해 각 모형하에서 소득과 거리를 고려하지 않은 모형으로서 단순히 αl = γ0와 β1 = β2 =…= βK =: β0를 가정하면, 로그우도함수 (8)을 이용하여 η∈{0, a, b}에 대해 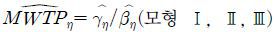 및
및 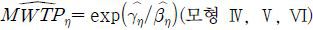 를 얻을 수 있다. 한편, 소득을 고려하지 않은 모형은 K = 1인 경우라 할 수 있다.
를 얻을 수 있다. 한편, 소득을 고려하지 않은 모형은 K = 1인 경우라 할 수 있다.
Ⅳ. 실증분석
1. 설문자료의 개요
실증분석을 위해 국립 부산과학관의 신축 건립 타당성 여부를 판단하기 위해 2010년에 시행한 CVM 설문자료를 이용하였다. 교육과학기술부는 부산광역시 기장군 동부산관광단지 개발지구 내에 국립과학관을 신축하는 안을 고려하였으며, 본 과학관의 편익을 추정하기 위해 전국을 대상으로 CVM 설문을 수행하였다. 먼저 개방형 질문을 통해 총 100가구의 응답자들에게 국립 부산과학관의 건립을 위한 WTP를 사전조사(pilot survey)한 후, 응답자료의 중앙값(median)을 바탕으로 본조사를 위해 1,000원부터 10,000원까지 총 7개의 제시금액을 결정하였다. 이렇게 결정된 제시금액은 전체 응답자를 무작위로 7개 그룹으로 나눈 뒤 각각 할당하였다. 본조사에서 지불의사를 묻는 질문은 양분선택형으로 구성하여, 해당 과학관의 건립을 위해 응답자가 소득세의 형태로 연간 제시금액만큼을 지불할 의사가 있는지를 물었다. 각 지역의 전체 인구를 대상으로 임의표본(random sample)을 도출하기 위해 각 지역 내의 인구 구성비를 고려하여 각 연령의 비율에 맞추어 표본 수를 할당하였다. 조사단위는 가구이며 일대일 대면조사를 통해 총 1,000개의 응답을 얻었다.
이들 응답 중 335가구는 지불의사가 있음을, 나머지 665가구는 지불의사가 없음을 표시하였다. 이때 ‘응답 거부’에 해당하는 표본을 제외하기 위해 지불의사가 없다는 응답자에게 지불의사가 없는 이유를 묻는 질문을 추가적으로 하였다. 응답 거부는 해당 질문에서 ‘이미 충분한 세금을 내고 있으므로 그 돈으로 사업을 진행해야 한다’(252개), ‘정부의 건립⋅운영 계획을 신뢰할 수 없다’(39개) 및 ‘판단할 만한 충분한 정보가 주어지지 않았다’(5개)의 문항을 선택한 경우에 해당된다. 이들을 제외하면 이용 가능한 관측치는 총 704개이며, 이들 중 경남 및 울산을 포함한 부산 인접지역(a)에서 335개, 기타 지역(b)에서 369개의 관측치를 얻었다. 제시금액별 WTP 응답의 분포는 <Table 3>에 나타난 바와 같다. 이때 가장 우측열에 유효표본 중 ‘예’로 응답한 비율이 표시되어 있는데, 이론이 설명하는 바와 같이 제시금액이 높아질수록 이 비율이 일반적으로 감소하는 것을 알 수 있다.
한편, 응답자의 소득별 분포는 <Table 4>와 같다. 먼저 설문에서는 가구당 월간 세후 소득을 10개의 구간으로 나누어 조사하였다. 분석에서는 표본의 개수를 고려하고 소득별 차이를 보기 위해 이들을 다시 고소득, 중소득 및 저소득의 세 가지로 구분(K = 3)하여 사용하였다. 표본의 개수가 충분히 많다면 소득그룹의 수를 늘려 보다 세밀하게 소득구간별 소득효과의 차이를 살펴볼 수 있으나, 주어진 자료는 최고 및 최저 소득구간으로 갈수록 표본의 개수가 급격히 줄어들어 소득그룹의 수를 늘릴 경우 통계적 유의성이 떨어지는 한계가 있다. 이와 같은 소득의 세 가지 구분은 <Table 4>의 우측에 표시되어 있는데, 표본의 절반 정도가 중소득으로 분류되었으며, 고소득과 저소득은 각각 나머지의 절반 정도로 배분되었음을 알 수 있다. 한편, 설문의 WTP 금액이 ‘연간’ 지불의사임을 감안하여 <Table 4>의 최우측열에 표본 내 각 소득구간의 전국단위 연소득 중앙값을 표시하였다. 부산 인접지역 및 기타 지역의 연소득 표본 중앙값은 각각 3,731만원과 4,024만원이었다. 소득의 평균 대신 중앙값을 제시한 이유는 최하위 구간과 최상위 구간이 각각 하방과 상방으로 열려 있기 때문에 평균을 구할 수 없으며, 중앙값이 극단치에 대해 강건한 통계량이기 때문이다.
마지막으로 설문지는 응답자 거주지의 동⋅리 단위 정보를 포함하고 있다. 이를 이용하여 응답자의 거주지와 대상지까지의 직선거리를 구하여 거리자료로 사용하였다.
2. 모집단의 분포
지역별 가구 수는 2010년 인구주택총조사 결과를 이용하였다. 한편, 전국소득자료는 통계청의 가계동향조사 및 가계금융복지조사를 이용하였다. 가계동향조사자료는 전국의 소득 10분위별 가구당 평균소득을 공개하고 있다. 이를 이용하여 전국단위 모집단의 소득분포를 얻을 수 있다. 하지만 가계동향조사는 표본의 수가 상대적으로 적어 하부지역 단위 평균 및 분산의 신뢰도가 떨어지므로 πk(l)을 구하는 근거로 활용하기에는 부적절하다. 따라서 πk(l)을 얻기 위하여 가계금융복지조사자료를 이용하였다. 가계금융복지조사는 가장 세부적인 정보로서 광역시⋅도별로 취합한 자료의 분석 결과를 제공한다. 이에 근거하여 πk(l)과 N(l)은 광역시⋅도별 정보를 이용하도록 한다. 다만, 가계금융 복지조사자료는 광역시⋅도별 소득의 표본평균치는 공개하고 있으나 분위별 관측치는 공개하지 않고 있다. 이에 차선의 방법으로 광역시⋅도별 소득이 로그정규분포(lognormal distribution)를 따른다고 가정한 후, 한국노동패널의 소득표본의 지역별 분산을 이용하여 πk(l)을 얻었다.
한편, 지역 간 물가수준의 차이를 고려하여 소득을 보정해야 하는 문제를 제기할 수 있으나, 이상호(2010)의 연구에 의하면 우리나라 지역 간 물가 차이가 임금증가에 미치는 효과는 미미한 것으로 나타났다. 따라서 본 연구에서는 물가를 보정한 실질소득이 아닌 명목소득을 소득의 기준으로 삼는다.
3. 분석 결과 및 논의
제Ⅱ장의 모형을 이용하여 추정치를 얻은 뒤, 가구당 MWTP의 신뢰구간은 Krinsky and Robb(1986)의 방법을 이용하여 구하였다. 비선형의 로그우도함수로부터 추정된 모수값을 선형 근사(linear approximation)하여 구해진 MWTP의 신뢰구간은 정확하지 못한 값을 가진다고 알려져 있으므로 시뮬레이션을 통해 보다 정확한 값을 구하는 것이다(보다 자세한 내용은 Park, Loomis, and Creel[1991], pp.65~67 참조). 본고에서는 5,000번의 시뮬레이션을 통해 신뢰구간을 구하였는데, 거리-소멸 효과를 고려한 경우에는 각각의 주어진 거리에 대해 매 5,000번의 시뮬레이션을 함으로써 전 영역에 대한 신뢰구간을 구하였다.
그리고 추정치의 신뢰도(credibility) 및 강건성(robustness)을 다양한 가정을 통해 확인하였다. 먼저 소득 및 거리-소멸 효과를 전혀 고려하지 않은 경우(Table 5), 표본을 인접지역과 기타 지역으로 나누어 불완전하게 거리-소멸 효과를 고려한 경우(Table 6), 그리고 소득효과만을 고려한 경우(Table 7) 및 거리-소멸 효과만을 고려한 경우(Table 8), 마지막으로 소득효과와 거리-소멸 효과를 모두 고려한 경우(Table 9)를 살펴보았다.7 거리-소멸 효과를 고려하지 않은 모든 경우(불완전하게 거리-소멸 효과를 고려한 경우 포함)에 대해 모형 Ⅰ, Ⅱ, Ⅲ과 모형 Ⅳ, Ⅴ, Ⅵ은 서로 동일한 결과를 보인다.
<Table 5>~<Table 7>의 추정 결과에서는 모든 추정치가 기대한 부호로, 통계적으로 매우 유의하게 얻어졌다. 불완전하게 거리-소멸 효과를 고려한 경우에는 <Table 6>에서 보는 바와 같이 인접지역의 평균지불의사액(MWTPa)이 기타 지역의 것(MWTPb) 보다 높게 구해졌음을 알 수 있다. 그리고 소득효과를 고려한 경우 <Table 7>에 나타난 바와 같이 MWTP는 소득이 증가할수록 점차 증가하는 경향을 보임을 알 수 있다. 한편, 모형설정오류에 의한 비정형적인(irregular) 효용함수를 가정한 임의적 모형 Ⅳ, Ⅴ와 Ⅵ의 결과는 상응하는 기타 모형들과 매우 다른 추정 결과를 나타냄을 알 수 있다.
<Table 5>
Estimation Results: No Income Effect and No Distance-Decay Effect
Note: Numbers in the parentheses are t values and those in the brackets are 95% confidence intervals.
<Table 6>
Estimation Results: Incomplete Distance-Decay Effect
Note: Numbers in the parentheses are t values and those in the brackets are 95% confidence intervals.
<Table 7>
Estimation Results: Income Effect
Note: Numbers in the parentheses are t values and those in the brackets are 95% confidence intervals.
거리-소멸 효과를 고려한 경우의 추정 결과는 <Table 8>에 제시되어 있다. 이때 모형 Ⅰ과 Ⅳ에서는 거리-소멸 효과가 95% 신뢰수준에서 통계적으로 유의하지 않게 나타났다. 이는 거리-소멸 효과가 선형적으로 나타난다는 가정이 적절하지 못함을 보여준다. 반면, 모형 Ⅱ와 Ⅴ에서 모든 추정치가 기대한 부호를 가지며 통계적으로 유의한 결과를 보인 것으로 보아 거리-소멸 효과는 지수적으로 감소하는 형태가 적절한 것으로 보인다. 이때에도 구조모형 Ⅱ와 임의적인 모형 Ⅴ의 결과는 상이한 추정 결과를 나타내었다. 또한 펼쳐진 지수함수를 가정한 모형 Ⅲ과 Ⅵ에서는 γ1과 γ2가 95% 신뢰수준에서 통계적으로 유의하게 추정되지 않았으며, 이들을 0이라 하면 모형 Ⅲ, Ⅵ은 각각 모형 Ⅰ, Ⅳ와 동일해진다. 따라서 소득효과를 고려하지 않고 거리-소멸 효과만을 상정한다면 모형 Ⅱ가 자료를 가장 잘 설명하는 구조모형이라 할 수 있다.
[Figure 1]은 이와 같은 거리-소멸 효과를 거리에 따라 도식화한 것이다. 먼저 모형 Ⅰ과 Ⅳ, Ⅱ와 Ⅴ, 그리고 Ⅲ과 Ⅵ은 서로 유사한 결과를 보인다. 지수 형태의 거리-소멸 효과를 고려한 모형 Ⅱ와 Ⅴ에서는 거리가 짧은 경우 MWTP가 급격히 감소하다가 거리가 늘어날수록 완만한 감소의 경향을 보이고 있다. 이를 모형 Ⅰ 및 Ⅲ과 각각 비교하면 선형의 거리-소멸 효과를 가정한 경우 거리가 짧을 때의 급격한 기울기를 설명하지 못하고 있음을 알 수 있으며, 이에 따라 통계적 유의성이 떨어짐을 유추할 수 있다. 한편, 이때 점선으로 표시된 것은 95% 신뢰구간인데, 선형의 거리-소멸 효과를 가정한 경우(모형 Ⅰ과 Ⅲ) 신뢰구간이 거리가 매우 가깝거나 큰 경우에 상대적으로 넓게 구해짐을 알 수 있다. 이는 MWTP가 거리에 대하여 선형으로 감소하므로 짧은 거리에서는 MWTP 값이 크기 때문에, 그리고 거리가 길어지면 거리에 대한 모수 γ1의 변동폭이 크게 반영되기 때문이다.
마지막으로 소득효과와 거리-소멸 효과 모두를 고려한 추정 결과가 <Table 9>에 나타나 있다. 이때 거리-소멸 효과는 앞서 <Table 8>의 결과와 유사하게 얻어졌으며, 소득의 영향 역시 <Table 7>과 동일한 경향을 보인다. 소득효과와 거리-소멸 효과 모두 통계적으로 유의하게 나타났으며, 특히 구조적 모형에 부합하는 모형 Ⅱ의 결과가 신뢰할 만할 것이다.
<Table 9>
Estimation Results: Both Income and Distance-Decay Effects
Note: Numbers in the parentheses are t values.
[Figure 2]는 각 모형에서 얻어진 MWTP의 소득 및 거리별 변화를 보여준다. 예상한 바와 같이 소득이 높을수록 그리고 거리가 짧을수록 높은 지불의사액을 가짐을 알 수 있다. 그리고 모형 Ⅱ에서 고소득-중소득 간의 지불의사액 차이는 중소득-저소득 간의 차이보다 작게 구해졌는데, 이는 Diamond et al.(1993, p.42)이 지적한 바와 같이 한계 소득효과가 소득의 증가에 대하여 체감하는 경향을 설명한다. 따라서 소득효과를 보다 엄밀히 고려하고자 한다면 중소득 및 저소득 집단에서 보다 세부적인 구분을 할 필요가 있음을 확인할 수 있다.
총편익은 앞서 제Ⅱ장에서 논의한 방식으로 산정하였다. <Table 10>은 각각의 경우에 대해 각 모형이 추정한 총편익을 95% 신뢰구간과 함께 제시하고 있다. 모형 Ⅲ과 모형 Ⅵ의 경우 일부 모수 추정치가 통계적으로 유의하지 않게 얻어진 결과, 시뮬레이션에 의한 95% 신뢰구간의 상한이 지나치게 크게 구해지는 경우가 있었으며, 이들은 표시하지 않았다.
<Table 10>
Aggregated Willingness to Pay
Note: Numbers in the brackets are 95% confidence intervals.
가장 신뢰할 만한 모형 Ⅱ에서 여러 가지 경우를 비교한 결과, 소득효과와 거리-소멸 효과를 모두 고려한 경우에 비해 이들 모두를 고려하지 않은 경우 연간 총편익이 약 14.5%(84.9억원) 높게 추정되며, 거리-소멸 효과만을 불완전하게 고려한 경우에는 약 6.8%(39.9억원) 높게 추정됨을 알 수 있다. 한편, 소득효과만을 고려한 경우 약 16.6%(97.2억원)의 과다추정이, 거리-소멸 효과만을 고려한 경우에는 약 1.3%(7.7억원)의 과다추정이 이루어진 것으로 보아 실증분석 자료의 경우 소득효과보다 거리-소멸 효과가 지배적(dominant)임을 확인할 수 있다.
소득효과와 거리-소멸 효과를 모두 고려한 경우에 상대적으로 작은 총편익 추정치를 얻은 것은 CVM 설문에 의한 편익의 추정이 보수적으로 이루어져야 한다는 NOAA 패널의 권고에 부합하는 결과이며, 일반적으로 비용편익분석에서도 사업의 불확실성이 많은 경우 보수적인 추정이 선호된다는 점에서 바람직한 결과라 할 수 있다. 다만, 모집단의 소득분포에 대한 정보가 불충분한 상태에서 앞서 설명한 바와 같이 차선책을 택한 점을 상기하면, 향후 유사한 연구를 수행함에 있어 정확한 총편익의 산정을 위해 모집단의 세부지역 단위별 소득분포에 대한 정보의 공개가 반드시 요구된다 하겠다.
Ⅴ. 시뮬레이션
본 장에서는 지금까지 논의한 소득효과와 거리-소멸 효과를 고려하지 않는 경우 어떤 결과가 예상되는지를 시뮬레이션을 통해 살펴보고자 한다. 먼저 총편익의 추정치를 참값과 비교하여, 모형의 선택에 따라 추정치가 참값과 얼마나 차이가 있는지를 검증함으로써 잘못된 모형을 선택하였을 경우의 왜곡의 크기를 알아본다. 한편, 공공시설의 입지에 따른 총편익의 추정치를 비교함으로써 지역균형발전의 관점에서 모형의 선택이 어떤 함의를 가지는지를 살펴본다.
1. 시뮬레이션의 개요
분석의 편의를 위해 1차원 공간 [0, L]을 고려하여, 0과 L의 위치에 새로운 공공시설을 건립하는 경우를 비교하기로 한다. 이때 L = 500㎞라 하고 두 경우 모두 인접지역은 해당 시설에서 150㎞까지의 범위로 설정한다. 즉, 공공시설의 위치 lF 가 0과 L인 경우 인접지역은 각각 [0,150]과 [350,500]이며, 나머지 구간은 비인접지역이다. 그리고 모집단은 총 가구 수가 1천만이며 [0, L]의 범위에 고르게(uniformly) 분포되어 있다고 가정하고, 소득분포는 고소득 및 저소득 두 그룹으로 나누어 [Figure 3]과 같다고 하자. 즉, [0, L]의 공간에서 우측으로 갈수록 평균소득이 증가하는 경우이다.
한편, 모형 Ⅱ가 옳은 모형이라고 하고 모수의 참값은  = 2,
= 2, 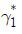 =−0.2,
=−0.2, 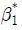 = 0.3 및
= 0.3 및 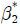 = 0.2라 하며, 제시금액은 <Table 3>에서와 같이 7개를 무작위로 배분하기로 한다. 이때 총편익의 참값은
= 0.2라 하며, 제시금액은 <Table 3>에서와 같이 7개를 무작위로 배분하기로 한다. 이때 총편익의 참값은
과 같이 계산하여 각각 296.55억원과 304.57억원으로 얻어진다.8 따라서 시뮬레이션 모형은 다른 모든 조건이 동일한 경우 평균소득이 높은 곳에 공공시설을 건립하는 경우 총편익이 2.7%(8.02억원) 높게 산정됨을 알 수 있다.
이때 거리-소멸 효과의 평균치(l = 250에 해당)가 모든 가구에 동일하게 작용한다고 가정함으로써 거리-소멸 효과를 고려하지 않고 소득효과만을 고려하면 총편익은 두 경우 모두 276.20억원이다. 물론 거리-소멸 효과를 완전히 배제한 모형에 의한 추정 결과는 모수가 변화할 수 있어 이 값을 앞서의 두 총편익값과 직접 비교하는 것은 의미가 없으나, 고소득 가구와 저소득 가구의 상대적 기여도는 비교 가능하다. 소득효과만을 고려한 경우 고소득 가구의 기여분은 시설의 위치와 관계없이 총편익의 60%이며, 두 효과 모두를 고려한 경우는 0의 위치에 건립하는 경우 총편익의 56.8%, L의 위치에 건립하면 총편익의 63.2%가 고소득 가구의 기여분이 된다. 이는 소득효과와 거리-소멸 효과가 동시에 작용하여 나타난 효과이며, L에 공공시설을 건립하는 경우 거리-소멸 효과에 의해 L에 가까울수록 총편익에 대한 기여도가 높아지는데, 이때 상대적으로 높은 WTP를 가지는 고소득 가구의 비율이 증가하기 때문이다.
본 시뮬레이션을 통해 검증하고자 하는 것은 1) CVM 설문이 모수의 참값을 잘 복원해 내는지와 2) 소득효과 및 거리-소멸 효과가 있는 상황에서 분석모형이 이 효과들을 어떻게 고려하는지에 따라 총편익의 추정치에 어떤 차이가 발생하는지의 두 가지로 나눌 수 있다. 이들 중 소득효과와 거리-소멸 효과가 있는 상태에서 이들을 고려하지 않은 경우 총편익 추정치에 어떤 영향이 있는지를 살펴보기 위해 ① 소득효과와 거리-소멸 효과를 모두 고려한 경우(full model), ② 소득효과를 고려하지 않고 거리-소멸 효과만을 불완전하게 고려한 경우(incomplete model), 그리고 ③ 소득효과 및 거리-소멸 효과를 고려하지 않은 경우(naive model)의 세 가지 모형을 비교하고자 한다. 이때 모형 ①, ② 및 ③에 의한 총편익의 산정은 각각 식 (3), (5) 및 (4)를 따른다. 물론 이들 세 가지 모형 중 ①의 올바른 모형이 가장 정확한 추정치를 보일 것이며, 시뮬레이션을 통해 살펴보고자 하는 것은 모형설정오류를 부여한 ②의 불완전한 모형과 ③의 단순한 모형에 의한 추정치와 참값 간의 차이이다. 특히 실증연구에 흔히 사용되는 단순한 모형 ③을 사용했을 때의 문제점을 규명함으로써 연구자들이 주의해야 할 점을 밝히고자 한다.
이때 특정 표본가구는 공공시설과의 거리, 소득 및 관측되지 않는 오차로 규정된다. 먼저 CVM 설문의 모수 참값 복원 가능성을 검증하기 위해 무작위로 (500, 1,000, 100,000)개의 거리를 뽑고, 뽑힌 위치에 해당하는 소득분포로부터 해당 개수만큼의 소득을 추출(draw)한다. 마지막으로 평균이 0이고 분산이 1인 로지스틱 분포로부터 오차항을 역시 해당 개수만큼 추출한다. 이와 같이 뽑힌 가구의 거리와 소득, 모수의 참값 및 무작위로 택한 제시금액을 이용하여 효용격차를 구하고, 이를 추출된 오차와 비교하여 해당 제시금액에 대한 ‘예/아니오’의 응답표본을 구한다. 이들 표본을 대상으로 소득효과 및 거리-소멸 효과를 고려한 모형을 통해 lF = 0인 경우와 lF = L인 경우에 대해 각각 제Ⅲ장에서 소개한 방식으로 추정된 모수 추정치와 참값을 비교한다. 이때 1번의 시뮬레이션에 이용된 표본의 수를 s, 시뮬레이션 수를 S라 하면 s = (500, 1,000, 100,000)이고, S = 1이다.
한편, 소득효과 및 거리-소멸 효과를 고려한 모형과 고려하지 않는 모형을 비교하는 경우, 본 연구에서 상정한 CVM 설문방식을 이용하기 위해 lF = 0인 경우 시뮬레이션은 다음과 같이 행한다. 먼저 인접지역인 [0, 150]의 구간에서 무작위로 하나의 거리를 추출한다. 이때 앞서와 같이 뽑힌 위치에 해당하는 소득분포로부터 소득을 추출하고, 오차항을 추출한 뒤, 무작위로 선택된 제시금액에 대한 ‘예/아니오’의 응답표본을 구한다. 이와 같은 과정을 500번 반복하고, 비인접지역인 [150, 500]의 구간에 대해서도 역시 500번 반복하여 총 1,000개의 표본을 얻는다. 이들 표본을 대상으로 소득효과 및 거리 −소멸 효과를 완전히 고려한 올바른 모형 ①과 그렇지 않은 모형 ②와 ③에 대해 모수의 값을 추정하고, 이를 이용한 총편익의 추정치를 구할 수 있다. 마지막으로 해당 과정을 10,000번 반복하여 총편익 추정치의 신뢰구간을 구하여 세 모형을 비교할 수 있다. 본 장에서 최종적으로 비교하고자 하는 것은 상대적으로 평균소득이 높은 곳과 낮은 곳에 건립될 공공시설들이므로, lF = L인 경우에 대하여 동일한 방식으로 총편익을 구한 뒤 앞서 구한 추정치와 비교하도록 한다. 이 경우에는 s = 1,000이고, S = 10,000이다.
2. 시뮬레이션 결과 및 논의
먼저 CVM 설문을 이용한 소득효과와 거리-소멸 효과 관련 모수 추정치의 적합성(validity)을 살펴보기 위한 시뮬레이션 결과는 <Table 11>에 표시된 바와 같다.
<Table 11>
Simulation Results: Checking Validity of Model
Note: Numbers in the parentheses are t values.
표본의 수가 적은 경우(s = 500) 일부 모수 추정치들은 통계적으로 유의하지 않고 총편익의 추정치 역시 참값과 크게 다름을 알 수 있다. 표본이 1,000개인 경우 모든 모수 추정치들이 통계적으로 유의하게 얻어졌으며, 총편익 역시 참값과 유사하게 구해짐을 알 수 있다. 물론 이는 1번의 시뮬레이션 결과이므로(S = 1) 표본의 개수가 비교적 작은 경우 추출된 표본에 따라 추정치들이 매번 변화하며, 이는 실제 CVM 설문과정에서 보다 정확한 값을 추정하기 위해 사전조사를 통해 제시금액을 조정하거나 시설에 대한 충분한 정보를 제공하는 것이 중요함을 시사한다. 그러나 표본이 매우 많은 경우(s = 100,000)에는 표본선택과 무관하게 모든 모수와 총편익의 추정치가 참값을 잘 복원해 냄을 보았을 때 모형이 적합함을 확인할 수 있다.
다음으로 <Table 12>는 앞서 상정한 ①, ② 및 ③의 모형을 비교하기 위한 시뮬레이션 결과(s = 1,000, S = 10,000)를 나타낸다. 이때 각 결과는 시뮬레이션 이후 얻어진 평균값과 95% 신뢰구간을 표시하였다. 이때 세 모형 모두에 대해 평균적으로
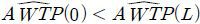 을 얻어, 총편익의 추정치가 참값과 같은 방향으로 얻어졌음을 알 수 있다. 각 모형별 시뮬레이션 결과를 살펴보면, 먼저 소득효과와 거리-소멸 효과를
모두 고려한 올바른 모형 ①의 경우 예상한 바와 같이 모수 및 총편익의 참값을 잘 복원해 냄을 알 수 있다. 거리-소멸 효과를 불완전하게 고려하는
모형 ②에서는 두 입지 모두에 대하여 예상한 대로 인접지역의 가구당 평균지불의사액 MWTPa가 비인접지역의 MWTPb보다 크게 추정되었다. 그리고 lF = 0인 경우에는 소득효과와 거리-소멸 효과가 서로 상쇄되어 lF = L인 경우보다 인접지역과 비인접지역 간 가구당 MWTP의 차이가 작게 얻어진 것도 예상과 일치하는 결과이다. 그러나 본 모형의 문제는 두 경우 모두
총편익이 과소추정되었다는 점이다. 소득효과 및 거리-소멸 효과를 전혀 고려하지 않은 단순한 모형 ③의 경우에는 두 입지 모두에서 총편익을 과다추정하는
결과를 보였다.
을 얻어, 총편익의 추정치가 참값과 같은 방향으로 얻어졌음을 알 수 있다. 각 모형별 시뮬레이션 결과를 살펴보면, 먼저 소득효과와 거리-소멸 효과를
모두 고려한 올바른 모형 ①의 경우 예상한 바와 같이 모수 및 총편익의 참값을 잘 복원해 냄을 알 수 있다. 거리-소멸 효과를 불완전하게 고려하는
모형 ②에서는 두 입지 모두에 대하여 예상한 대로 인접지역의 가구당 평균지불의사액 MWTPa가 비인접지역의 MWTPb보다 크게 추정되었다. 그리고 lF = 0인 경우에는 소득효과와 거리-소멸 효과가 서로 상쇄되어 lF = L인 경우보다 인접지역과 비인접지역 간 가구당 MWTP의 차이가 작게 얻어진 것도 예상과 일치하는 결과이다. 그러나 본 모형의 문제는 두 경우 모두
총편익이 과소추정되었다는 점이다. 소득효과 및 거리-소멸 효과를 전혀 고려하지 않은 단순한 모형 ③의 경우에는 두 입지 모두에서 총편익을 과다추정하는
결과를 보였다.
<Table 12>
Simulation Results: Model Comparison (s = 1,000, S = 10,000)
Note: Numbers in the brackets are 95% confidence intervals.
시뮬레이션 결과로 얻어진 총편익 추정치의 평균값을 비교하면, 올바른 모형 ①은 lF = 0인 경우와 lF = L인 경우 총편익의 참값과 각각 0.13%와 0.03%의 차이만을 보여 매우 정확한 추정 결과를 도출하였음을 알 수 있다. 불완전한 모형 ②의 경우에는
평균적으로 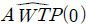 은 AWTP*(0)보다 4.32%,
은 AWTP*(0)보다 4.32%, 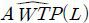 은 AWTP*(L)보다 4.86% 각각 작게 구해졌다. 한편, 단순한 모형 ③의 경우에는 평균적으로
은 AWTP*(L)보다 4.86% 각각 작게 구해졌다. 한편, 단순한 모형 ③의 경우에는 평균적으로 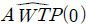 은 AWTP*(0)보다 2.06%,
은 AWTP*(0)보다 2.06%, 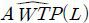 은 AWTP*(L)보다 4.53% 각각 크게 얻어졌다. 이때 두 입지에 대한 총편익 추정치 간의 차이
은 AWTP*(L)보다 4.53% 각각 크게 얻어졌다. 이때 두 입지에 대한 총편익 추정치 간의 차이 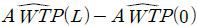 는 각각 (7.8, 6.3, 15.8)억원이다.
는 각각 (7.8, 6.3, 15.8)억원이다.
모형 ②와 ③에서 점근적(asymptotic) 총편익 추정치를 살펴보기 위해 S = 1 및 s = 100,000하에서 시뮬레이션을 수행한 결과, 모형 ②로부터는 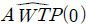 = 294.4억원과
= 294.4억원과 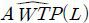 = 300.4억원을 얻었고, 모형 ③으로부터는
= 300.4억원을 얻었고, 모형 ③으로부터는 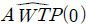 = 310.3억원과
= 310.3억원과 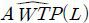 = 326.7억원을 얻었다. 따라서 모형 ②의 과소추정과 모형 ③의 과다추정의 문제는 상존하는 것으로 보인다. 이때 모형 ②에서는 점근적으로
= 326.7억원을 얻었다. 따라서 모형 ②의 과소추정과 모형 ③의 과다추정의 문제는 상존하는 것으로 보인다. 이때 모형 ②에서는 점근적으로 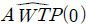 은 AWTP*(0)보다 0.74%,
은 AWTP*(0)보다 0.74%, 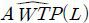 은 AWTP*(L)보다 1.38% 각각 작게 구해졌다. 한편, 모형 ③에서는 점근적으로
은 AWTP*(L)보다 1.38% 각각 작게 구해졌다. 한편, 모형 ③에서는 점근적으로 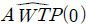 은 AWTP*(0)보다 4.62%,
은 AWTP*(0)보다 4.62%, 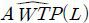 은 AWTP*(L)보다 7.26% 각각 크게 얻어졌다. <Table 11>의 올바른 모형 ①로부터
은 AWTP*(L)보다 7.26% 각각 크게 얻어졌다. <Table 11>의 올바른 모형 ①로부터 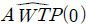 = 295.7억원과
= 295.7억원과 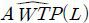 = 304.5억원으로 추정됨을 알았으므로 두 입지에 대한 총편익 추정치 간의 차이는 점근적으로 각각 (8.8, 6.0, 16.4)억원이다.
= 304.5억원으로 추정됨을 알았으므로 두 입지에 대한 총편익 추정치 간의 차이는 점근적으로 각각 (8.8, 6.0, 16.4)억원이다.
이와 같은 시뮬레이션 결과로부터 알 수 있는 것은 소득효과와 거리-소멸 효과가 존재하는 상황에서 거리-소멸 효과만을 불완전하게 고려한 모형을 사용하면 총편익의 추정치는 참값에서 벗어나 과소추정되는 결과를 얻을 수 있다는 점이다. 한편, 동일한 상황에서 소득효과 및 거리-소멸 효과를 전혀 고려하지 않는다면 반대로 총편익이 과다추정되었다. 이때 왜 불완전한 모형 ②에서는 과소추정, 단순한 모형 ③에서는 과다추정의 결과를 얻었는지는 분명치 않다. <Table 12>의 결과는 10,000번의 시뮬레이션에 의한 결과이므로 표본선택에 의한 오차라고 볼 수는 없으며, 실제로 s = 1,000에서 S = 5,000과 S = 10,000인 경우의 시뮬레이션 결과는 매우 유사하였다. 앞서 점근적 추정치의 비교에 의해서도 유사한 과소/과다 추정의 문제를 확인하였으며, 인접지역과 비인접지역을 고려하지 않은 표본 수의 배정 역시 추정치에는 영향을 주지 않는다. 제Ⅳ장의 분석 결과 얻어진 <Table 10>에서 소득효과와 거리-소멸 효과를 모두 고려하지 않은 모형에 의한 총편익 추정치가 불완전하게 거리-소멸 효과만을 고려한 모형에 의한 추정치보다 크게 나타나는 것으로 보아(모형 Ⅰ, Ⅱ, Ⅲ에서 662억원과 617.1억원), 실증분석에 사용된 자료에 소득효과 및 거리-소멸 효과가 실제로 존재하는 경우 참값을 모르는 경우라도 과소/과다 추정될 수 있는 경향은 염두에 두어야 할 것이다. 이에 대한 증명 및 추가적인 논의는 본 연구의 범위를 넘어서는 것으로 향후 연구과제로 남기기로 한다.
3. 지역균형발전에의 함의9
본 절에서는 시뮬레이션 결과를 통해 소득효과 및 거리-소멸 효과의 고려가 지역균형발전의 관점에서 가지는 함의가 무엇인지 논하고자 한다. 지역균형발전을 정책적으로 중요시한다면 상대적으로 낙후된 지역에 공공시설의 건립이나 인프라 투자가 보다 활발히 이루어지도록 해야 할 것이며, 일차적으로 비용편익분석상에서 최소한 낙후된 지역이 불공정한 손해를 입지는 않아야 할 것이다. 상대적 지역낙후도의 척도가 되는 것은 지역내총생산(gross regional domestic product: GRDP) 또는 지역 내 평균소득 등이 될 수 있다. 따라서 해당 관점에서 CVM의 결과로 얻어진 총편익 산정방식이 평균소득이 높은 곳에 공공시설을 건립하는 경우 상대적으로 과도하게 높은 총편익 추정치를 얻도록 설정되었다면 이는 지역균형발전을 저해하는 방향, 다시 말해 지역 간 격차를 확대하는 방향으로 설정된 것이므로 재고가 필요하다.
앞서 살펴본 바와 같이 시뮬레이션 모형은 다른 모든 조건이 동일한 경우 평균소득이 높은 곳(lF = L)에 공공시설을 건립하는 경우 lF = 0인 경우에 비해 총편익의 참값이 약 8억원 높게 산정되었으나 소득효과 및 거리-소멸 효과를 전혀 고려하지 않는다면 총편익 추정치의 차이가 약 16.4억원으로 나타나는 것으로 보아 지역균형발전의 관점에서 바람직하지 못함을 알 수 있다.10 물론 이는 소득효과와 거리-소멸 효과가 존재하는 상황에서 이들이 무시되었을 때에만 발생하는 왜곡이므로 실제 CVM 설문자료를 분석하는 경우에는 해당 효과들의 존재 여부를 검증하는 절차가 선행되어야 할 것이다. 이와 같은 절차를 거치지 않고 소득효과와 거리-소멸 효과를 고려하지 않는 모형을 사용한다면, 공공시설의 건립에 있어 지역균형발전이 중요한 정책적 판단요소인 경우 비용편익 분석에 의한 경제성 분석과 더불어 지역균형발전을 추가적으로 고려하는 것이 바람직할 것이다. 따라서 현행 예비타당성조사 시 일반적으로 소득효과와 거리-소멸 효과를 고려하지 않는 CVM 모형을 사용하지만 최종적으로 종합판단을 위한 분석적 계층화법(Analytic Hierarchy Process: AHP)의 구조상 제1계층에서 경제성 분석(비용편익분석), 정책적 분석 및 지역균형발전을 동일한 위상으로 고려하고 있는 것은 적절한 방식이라 할 수 있다.11
Ⅵ. 결론 및 정책제언
본고는 조건부가치측정법을 이용하여 공공시설의 신설에 따른 편익을 산정하고 이를 비용편익분석에 이용함에 있어 중요한 총편익의 산정을 보다 엄밀히 수행하는 방법을 제시하였다. 먼저 구조적 효용격차모형을 이용하여 소득효과 및 거리-소멸 효과의 크기를 직접 추정한 뒤, 모집단의 경험분포를 이용하여 보다 정확한 총편익을 산정하고자하였다. 이때 거리-소멸 효과의 형태에 대한 가정들과 다양한 경우를 고려한 추정을 통해 산정된 총편익의 변화를 비교하였다. 실제 CVM 설문자료를 이용한 추정 결과 지불의사액에 대한 소득효과 및 거리-소멸 효과가 존재함을 확인하였으며, 총편익의 산정시 이들을 고려하지 않는 경우 산정된 총편익의 값이 크게 달라질 수 있음을 보였다.
이에 본고는 조건부가치측정법을 비용편익분석에 이용하는 경우 총편익의 산정에 있어 주의를 기울여야 함을 강조한다. 비용편익분석에 있어 총비용의 추정이 정확히 이루어진다 하더라도 가구당 지불의사액의 추정 및 이들을 합산하여 총편익을 산정하는 방식이 옳지 못할 경우 편익/비용(B/C) 비율12이 크게 달라질 수 있기 때문이다. 특히 B/C 비율이 1 근처에 있는 경우 총편익 산정방식에 의해 공공시설 건립의 가부를 결정하는 기준이 정반대로 바뀔 수도 있다.
한편, 효용격차 구조모형을 따르지 않는 임의적인 모형설정오류를 부여하여 유사한 추정을 수행한 결과는 구조모형과 매우 큰 차이를 보임을 알 수 있었다. 따라서 총편익의 산정은 구조모형의 설정을 따르는 것이 바람직할 것이다.
그리고 정확한 총편익의 추정에 반드시 필요한 것은 정확한 모집단의 지역별 소득분포라 할 수 있다. 아무리 정교한 모형을 사용하여 소득효과와 거리-소멸 효과를 찾는다하더라도 모집단의 자세한 지역별 소득분포 자료가 없는 경우에는 산정된 총편익의 정확성이 감소될 수밖에 없다. 이에 본 연구가 제안하는 바는 우리나라 지역별 소득분포 자료의 구축이 시급하다는 점이다. 최근 통계청에서 지역별 평균소득을 공개하고 있으나 분위별 소득자료는 정보의 민감성 및 비정확성의 이유로 제공하지 않고 있다. 정보의 비정확성은 보다 많은 표본을 표집함으로써 해결할 수 있는 문제이다. 한편, 비록 지역별 소득분포가 민감한 자료라 하더라도 이들을 직접 비교하는 것이 아닌, 본 연구와 같이 합산에 이용하려는 연구자에게는 연구 목적으로 (식별정보를 삭제하는 등의 조치후) 제공되어야 할 것이다.
마지막으로 시뮬레이션을 통해 모형의 적합성을 검증하였으며, 시뮬레이션 결과 소득 효과 및 거리-소멸 효과가 존재하는 경우 이들을 고려하지 않거나 불완전하게 고려하는 경우 추정치가 참값과 상이하게 얻어지는 것을 확인하였다. 특히 소득효과 및 거리-소멸 효과를 전혀 고려하지 않는 모형은 지역균형발전의 관점에서 바람직하지 않은 결과를 보임을 확인하였다. 즉, 소득효과 및 거리-소멸 효과를 모두 무시한 모형을 사용하면 평균소득이 높은 지역에 공공시설을 건립하는 경우 총편익이 상대적으로 큰 폭으로 과다추정되는 결과를 얻음을 확인하였다. 따라서 공공시설의 건립에 있어 지역균형발전이 중요한 정책적 판단요소인 경우 해당 모형을 사용한다면 비용편익분석에 의한 경제성 분석과 더불어 지역균형발전을 추가적으로 고려하는 것이 바람직할 것이다.
Notes
SBDC와 DBDC 모형 중 어느 것이 우월한가에 대한 논의는 CVM 연구자들 사이에서 매우 활발히 연구되어 온 주제이며, 확정적인 결론은 내려지지 않은 상태이다. 기존의 연구 결과를 볼 때, DBDC 모형을 채택하면 SBDC 모형에 비해 통계적 효율성(statistical efficiency)을 높일 수 있으나(Hanemann, Loomis, and Kanninen[1991], pp.1257~1258) 내적 일관성(internal consistency), 출발점 편의, 유인 불일치(incentive incompatibility) 등의 편의를 초래할 가능성 또한 높아진다(McFadden[1994]; Herriges and Shogren[1996]; Whitehead[2002]). 따라서 비용편익분석을 위한 총편익 산정의 관점에서 충분한 표본을 확보한 경우, 통계적 효율성의 저하를 감수하더라도 편의를 줄이기 위해 SBDC 모형을 사용하는 것이 바람직할 것이다. 물론 본고의 논의는 DBDC 모형을 도입하여도 로그우도함수의 형태만 바뀔 뿐, 본질적으로 동일하다.
본 절에서는 본고의 완결성을 높이기 위해 일반적으로 정형화된 ‘효용격차모형’에 기반하여, 소득 및 거리를 고려한 본고의 표기법(notation)에 맞추어 소개하고자 한다. Hanemann(1984)에 의해 제안된 이와 같은 효용격차모형은 Cameron and James(1987) 등의 지출함수를 이용한 방식과 달리 간접효용 함수의 차이를 이용하여 힉스적 보상잉여(Hicksian compensating surplus), 즉 WTP를 추정하는 모형이다. McConnell(1990, p.34)은 이들 두 가지 방식이 쌍대관계(duality)에 있음을 지적하며, 두 모형 모두 기본적인 효용이론을 통해 유도됨을 보였다.
예를 들어 놀이공원이나 야구장과 같이 많은 사람들이 (상시적으로) 이용하는 시설의 경우, 주변에 사는 사람들이 시설은 가끔 이용하지만 늘 소음과 교통체증에 시달릴 수 있어 해당 시설이 거주지와 인접하여 들어서는 것에 반대할 가능성이 있다.
본 절은 기존에 소득과 거리를 고려하지 않은 CVM 연구들이 가지는 문제를 해결하는 과정에서 얻어진 부가적인 효과의 정책적 함의를 논하고자 하는 것으로, 본고가 지역균형발전을 저해하는 결과를 도출하는 CVM의 근본적 문제를 지적하고자 함은 아님을 밝힌다. 이와 같은 점을 지적해준 익명의 검토자에게 감사드린다.
References
, , , & (2006). The Aggregation of Environmental Benefit Values: Welfare Measures, Distance Decay and Total WTP. Ecological Economics, 60(2), 450-460, https://doi.org/10.1016/j.ecolecon.2006.04.003.
, , , & (2000). The Axford Debate Revisited: A Case Study Illustrating Different Approaches to the Aggregation of Benefits Data. Journal of Environmental Planning and Management, 43(2), 291-302, https://doi.org/10.1080/09640560010720.
, & (1987). Efficient Estimation Methods for ‘Closed-Ended’ Contingent Valuation Survey. Review of Economics and Statistics, 69(2), 269-276, https://doi.org/10.2307/1927234.
(2007). Investigating Distance Effects on Environmental Values: A Choice Modelling Approach. Australian Journal of Agricultural and Resource Economics, 51, 175-194, https://doi.org/10.1111/j.1467-8489.2007.00381.x.
, , , & (1995). Value for Money? A Contingent Valuation Study of Optimal Size of the Swedish Health Care Budget. Health Policy, 34(1), 135-143, https://doi.org/10.1016/0168-8510(95)00723-6.
(1984). Welfare Evaluations in Contingent Valuation Experiments with Discrete Responses. American Journal of Agricultural Economics, 66(3), 332-341, https://doi.org/10.2307/1240800.
, , & (1991). Statistical Efficiency of Double-Bounded Dichotomous Choice Contingent Valuation. American Journal of Agricultural Economics, 73(4), 1255-1263, https://doi.org/10.2307/1242453.
, & (1996). Starting Point Bias in Dichotomous Choice Valuation with Follow-up Questioning. Journal of Environmental Economics and Management, 30(1), 112-131, https://doi.org/10.1006/jeem.1996.0008.
, & (2003). Willingness to Accept, Willingness to Pay and the Income Effect. Journal of Economic Behavior & Organization, 51(4), 537-545, https://doi.org/10.1016/S0167-2681(02)00216-0.
, , , , & Characterizing Spatial Pattern in Ecosystem Service Values when Distance Decay Doesn’t Apply: Choice Experiments and Local Indicators of Spatial Association, 2011 AAEA & NAREA Joint Annual Meeting at Pittsburgh, Pennsylvania, Agricultural and Applied Economics Association, July 24~26 2011, 2011.
, & (1986). On Approximating the Statistical Properties of Elasticities. Review of Economics and Statistics, 68(4), 715-719, https://doi.org/10.2307/1924536.
(2006). Effects of Socio-Institutional and Emotional Factors of Japanese Farmland Rental Transactions. Journal of Agricultural and Applied Economics, 38(1), 33-46, https://doi.org/10.1017/S1074070800022057.
(1990). Models for Referendum Data: The Structure of Discrete Choice Models for Contingent Valuation. Journal of Environment Economics and Management, 18(1), 19-34, https://doi.org/10.1016/0095-0696(90)90049-5.
(1994). Contingent Valuation and Social Choice. American Journal of Agricultural Economics, 76(4), 689-708, https://doi.org/10.2307/1243732.
, , & (1991). Confidence Intervals for Evaluating Benefits Estimates from Dichotomous Choice Contingent Valuation Studies. Land Economics, 67(1), 64-73, https://doi.org/10.2307/3146486.
, & (1997). The Effect of Distance on Willingness to Pay Values: A Case Study of Wetlands and Salmon in California. Ecological Economics, 20(3), 199-207, https://doi.org/10.1016/S0921-8009(96)00080-8.
(2006, May 25). Survey Protocol and Income Effects in the Contingent Valuation of Public Goods: A Meta-Analysis. Ecological Economics, 57(3), 415-429, https://doi.org/10.1016/j.ecolecon.2005.04.019.
(2002). Incentive Incompatibility and Starting-Point Bias in Iterative Valuation Questions. Land Economics, 78(2), 285-297, https://doi.org/10.2307/3147274.