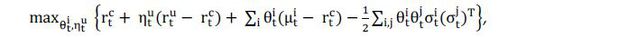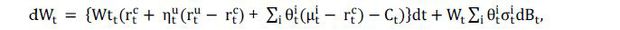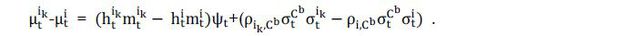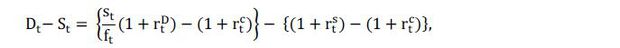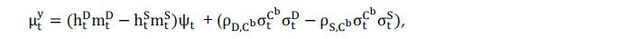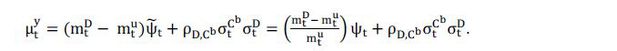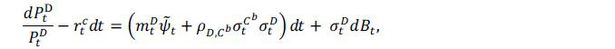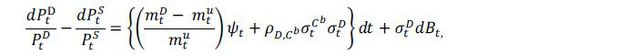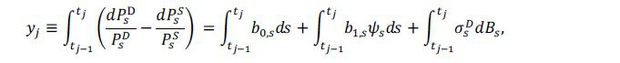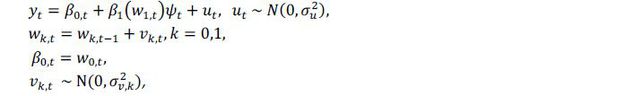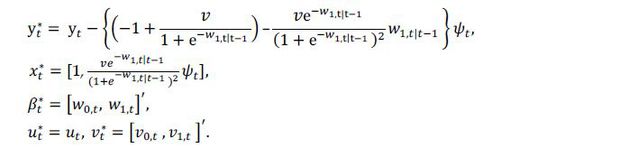Margin and Funding Liquidity: An Empirical Analysis on the Covered Interest Parity in Korea
Abstract
During the global financial turmoil in 2007-2008, deviation from the covered interest parity (CIP) between the Korean won and US dollar through the foreign exchange swap has escalated in its magnitude beyond 1,000bp in November 2008, and it still persists around 100bp level. In this paper, we examine a newly developed margin based asset pricing model using Kalman filter approach and show that the escalation of the CIP deviation is found to be significantly related to the global dollar funding illiquidity and country-specific funding conditions. Furthermore, we find evidence that the poor funding conditions (or higher margins) are driven by the general money market illiquidity and may lead to higher funding illiquidity, which suggests the reinforcing effects of the liquidity spiral. We also show that the supply of dollar liquidity and improved funding conditions help alleviate the deviations from the parity, however the persistent anomaly is found to be related to the high level of volatility in the FX swap market.
Keywords
Covered Interest Parity, Margin, FX Swap, Arbitrage, Shadow cost of Capital, 무위험 이자율 평형, 증거금, 외환스와프, 차익거래, 잠재자본비용
JEL Code
D3, D4, A7, A4, A0
Ⅰ. Introduction
During the global financial crisis in 2007-2008, the covered interest parity (CIP) is violated in many currency pairs, including South Korean won and US dollar. Not only the deviation from the parity was huge in its magnitude but it still persists up to the recent time. The covered interest parity, in essence, states that if free flow of capital is allowed, the duplicated dollar return using KRW/USD spot and forward should be equal to the dollar return. Basically, any sizable deviations from the parity implies that there exists a profitable arbitrage between the dollar spot and duplicated dollar derivatives (or FX swap), and as far as the arbitrage trade is allowed without constraints, the deviation from parity will automatically revert to zero profit level in a short period of time.
The question on what caused the deviation from the CIP has long been tackled by many authors. Largely, two types of explanations have been offered for the parity dislocations – limited arbitrage and risk compensation. Transaction costs (e.g. Frenkel and Levich (1977)), capital controls of government (e.g. Ito (1986)), and institutional weakness (e.g. Alper et al. (2007)) have been the major subjects of the literature on the arbitrage restrictions, while other studies on political risk (e.g. Aliber (1973)), liquidity risk (e.g. Bhar et. al (2004)), counter party risk (e.g. Baba et. al (2008), Baba and Packer (2009)), and funding liquidity risk (e.g. Coffey et. al (2009)) focus on the risky components imposed in the CIP deviations. In light of the recent development during the global financial crisis, funding liquidity risk (e.g. Coffey et. al (2009)) have been considered as the main cause of the deviation, considering the fact that the deviations are observed in many currency pairs involving the US dollar in the situation where dollar funding liquidity is scarce. Regarding the dislocations of the CIP relation between KRW and USD, similar types of explanations have been emerged. For example, structural imbalance between supply and demand in the forward market (e.g. Yang and Lee (2008) and Whang (2010)) and credit and liquidity risks (e.g. Ryu and Park (2008) and Yoo (2010)) are suggested as the main causes of the deviations. However, the question on how the deviation from the CIP has emerged in the recent global financial crisis has not been much investigated in the literature.
In this paper, we would like to shed some lights on the channel through which the global dollar funding crisis affect the CIP deviations in the KRW and USD pair based on a newly developed asset pricing model by Garleanu and Pedersen (2011) using our econometric methodology. They argue that the equivalent securities in normal times are no longer equivalent in bad times, especially when the funding liquidity is dried out. In a liquidity crisis, funding positions in risky assets are costly, and therefore, securities with higher margins1 (or harder funding conditions) will be discounted compared to lower margin securities. Especially, the funding liquidity premium will emerge and be determined by the security-specific funding conditions and general cost of funding, or equivalently referred to as the shadow cost of capital in their paper. The US dollar funding shortage driven by the liquidity crisis made the financial institutions become more cautious about funding the long positions in Korean won, and therefore, the CIP deviations emerged. Additionally, Korean financial institutions have experienced currency crisis because of the vast outflow of foreign capital, which results in the heightened counterparty risk. This will eventually deteriorate the Korea-specific funding condition and contribute further deviations of the CIP.
Their theoretical foundations are quite intriguing and have important implications on the liquidity crisis – the bad time when funding constraints are binding. Here, we discuss a bit about their theory to understand more on the CIP deviations. Basically, the funding constraint in their model is stating that the maximum capital use from funding their positions in risky assets cannot exceed his or her total wealth. If the constraint is binding, then additional need for a unit capital should reflect the funding liquidity premium, or the shadow cost of capital. They show that binding funding constraint leads to several interesting stylized facts. First, riskless interest rates for collateralized loans jump down during the financial crisis. This happens because the risk tolerant agents cannot borrow as they would like to and the risk averse agent should lend less than they wanted to. This can be induced by decreasing the riskless interest rates dramatically. Second, the spread between uncollateralized and collateralized loans increases. This occurs when the risk tolerant agents have binding margin constraints, and at the same time the risk averse agents do not participate in the uncollateralized loan market. Since the risk tolerant banks cannot borrow from the risk averse agent, the interbank uncollateralized loans should reflect the shadow cost of capital and require additional premium compared to the Treasury rates. Third, the Law of One Price can be violated and last long. This can be explained if two assets have different margin requirements while having the same cash flows. Under the binding margin constraints, the risk tolerant agent will require additional premium by the margin rate to the shadow cost of capital. In this case, higher margin securities will be priced in discount compared to lower margin securities. In other words, higher margin securities will cost more capital, and the price should reflect the shadow cost of capital in order to induce long position of the risk tolerant agent.
It is important to note that the margins in examining the CIP deviations are not directly observable. In order to find a suitable proxy, one might try to observe the “margin threshold2” in FX swaps, however, the margin on the FX swap involving a long position in the Korean government bond (or implied dollar loan3) is not necessarily equal to the margin threshold imposed in the FX swap. For example, a foreign bank (FB) enters into a sell&buy FX swap with a domestic bank (DB) in which the FB provides $10 million in exchange for ₩11,000 million now, and after three month, the FB repays ₩11,000 million and receives $11 million at the swap rate of ₩1,000 per unit of US dollar. Suppose that the margin threshold for the FB is set at $0.5 million while ₩77 million for the DB. Since margins are basically the difference between face value and collateral value of a security, the US dollar can be considered as a security with 5% margin while the Korean won with 7% margin. However, the 5% of margin (or haircut) set for FB is not actually the margin on the implied dollar loan because the collateral value of the FX swap and a long position in the government bond cannot be determined from the margin threshold. Assuming that there is a security dealer who can make a reverse repo4 agreement with FB so that he can make a collateralized loan to FB based on the implied dollar loan, the repo margin5 may be considered as the margin on the implied dollar. Since the margin on the implied dollar loan can be considered to reflect the credit worthiness and/or the liquidity of the Korean government bond, the higher worthiness or liquidity on the Korean government bond, the lower the margin will be, and therefore, funding for the long position in the implied dollar loan will be more accessible. Unfortunately, the empirical data on the reverse repo that would permit identification of the margin on the implied dollar loan is generally unavailable. Still, it is possible to extract the margin on the implied dollar loan based on our empirical procedure explained in the followings.
Especially, we extract a measure of the funding conditions (or the margin set for the implied dollar loan) using the time series properties of discrete approximation of a continuous time diffusion process for the equilibrium deviations of equivalent asset prices. Since the funding conditions for the implied dollar loan and US dollar libor loan is not directly observable, it is helpful to extract the funding conditions using the Kalman filter and investigate the relevance of the extracted funding conditions in explaining the deviations from CIP. The model that we consider to extract the funding conditions is a nonlinear standard state space model where the funding conditions can be exponentially deteriorated by some underlying latent factor. The state space model has attractive features that the extracted funding conditions based on the Kalman filter are stochastic, time-varying and predicted based on the information available up to the sample period. Therefore, once the unobservable funding conditions are extracted from data, further intriguing questions can be answered.
In this regard, it is also interesting to investigate whether the funding conditions are driven by general market illiquidity. Brunnermeier and Pedersen (2008) show that under certain circumstances, funding conditions (or margins) and market liquidity can be reinforcing, resulting to a margin spiral. When the shadow cost of capital is high or equivalently funding liquidity is low, high margin securities are less attractive because they cost more capital than lower margin securities. As a result, the market liquidity decreases. Moreover, expected future market illiquidity will increase the risk of financing a trade, and therefore, increasing the margins. As high margins increase market illiquidity, this leads to higher margins, which increase the shadow cost of capital further. The margin spiral emerges if market illiquidity increases margins.
Using daily data on interest rates, spot and forward exchange rates on KRW/USD from January 2007 to April 2010, we extract the relative scarceness in funding (relative margin) of three month US libor loan and implied dollar loan (Korean CD converted into US dollar at spot and re-converted into Korean won at forward rate). The relative margin differences are the differences between the implied dollar margin (mD) and US libor margin (mS) in proportion to the US libor margin; (mD−mS)/mS. According to our data, both the CIP deviations6 and the shadow cost of capital are positive in our sample period. Since the risk tolerant agent with tight funding constraint requires additional premium which is given by the product of the shadow cost of capital and margin requirements, positive deviations imply that the margin on the implied dollar loan is greater than the US libor loan. Our estimates for the relative margin differences show that the margin on the implied dollar loan is overall greater than the US libor loan, as expected. Since the margin in general on an asset determines the investor’s own capital required to trade the asset, higher margin in the implied dollar loan implies that the funding condition for the Korean currency is generally worse than the US libor loan. In fact, it is not surprising that the funding condition for the Korean won is commonly weaker than the US libor loan; the uncertainties regarding the macroeconomic prudence of Korea - especially the foreign currency liquidity - may restrict the upper bound of leverages that international investors can take for the long position in the Korean won and make the margin on the implied dollar loan stay at a higher level than the US libor.
Moreover, it is clearly seen from our empirical analysis that the increase in the relative margin differences magnified the increase in the deviation from the covered interest parity. After the Lehman bankruptcy, the shadow cost of capital is heightened and the higher margin security is further discounted so that the return on the implied dollar loan is expected to be much higher than the US libor loan, and as a result, the CIP deviation has been widen. Simultaneously, the relative margin differences have also been broaden and made the funding condition for the implied dollar loan to become increasingly degraded, magnifying the soaring the CIP deviation.
Also, we observe that the relative margin differences can quickly explode to a very high level and solely affect the CIP deviation. After the early October 2008, the shadow cost of capital has been dropped; the extreme dollar funding liquidity crisis has been passed away. However, the relative margin differences increased extremely fast in this period and made the CIP deviation record the highest level of 1,000bp. The fast increase in the relative margin differences seems to have happened in the situation when the funding condition in the implied dollar loan continues to be deteriorated while the funding condition in the US libor loan is improved. In other words, the CIP deviation can deepen fast during the crisis period if the global dollar liquidity is improved while the funding condition in Korean currency is worsened.
Meanwhile, we also find that the currency swap between central banks contribute in stabilizing the CIP deviation by decreasing the relative margin differences. On the late October 2008, the central bank currency swap line of $300 billion has been set. After a month, the relative margin differences took a downturn and dropped to the pre-Lehman level, and as a result, the CIP deviation also dropped down and started to stabilize. Since the margin on the implied dollar loan reflects the credit worthiness and/or the liquidity on the Korean government bond, lowered margin may imply that the government bond has regained its market confidence (or the collateral value has improved). In sum, it is evident from our analysis that the relative margin differences can magnify the increase of the CIP deviation in the liquidity crisis. It can quickly increase to the very high level and affect solely to the increase of the CIP deviations. Also, it seems that the central bank swap line help to improve the funding condition for the implied dollar loan, and finally decrease the CIP deviation.
Another contribution of our paper is that we examine the relationship between the relative margin and market illiquidity. As Brunnermeier and Pedersen (2008) argued, the margin spiral can emerge if the market illiquidity can disturb the funding condition (or increase the margin on the security). Recently, Coffey et al. (2009) suggest using the overnight MBS-Treasury repo spread as an empirical proxy for relative market illiquidity of the two repo securities. Considering that the repo market is one of the main sources of funding for global banks which can participate in the FX swap trade, the relative market illiquidity of the two assets can be considered as a measure for the general market illiquidity. Using three month MBS-Treasury spread, we find that the market illiquidity can actually explain the relative margin differences quite well and the margin spiral can emerge in the foreign currency swap market.
It should be emphasized here that the paper is not intended for explaining the CIP deviations in Korea before the global financial crisis. The CIP has been dislocated since early 2000’s, persisting its deviation significantly positive, which implies that foreign investment in the government bond via FX swap could be profitable. In fact, Korea has experienced vast amount of capital inflows until the global financial crisis, although the sudden outflows of capital during the crisis period has disturbed financial stability in Korea. Rather, the objective of this paper is to examine the ways in which the global funding liquidity crisis affects the FX swap market in Korea, in a structural economic model.
The rest of the paper is organized as follows. Section 2 describes the theoretical model investigated by Garleanu and Pedersen (2011), Section 3 accounts for our econometric methodology and empirical procedures to tackle some interesting questions regarding CIP deviations. Section 4 presents the main results and discussions. Then we conclude in Section 5.
Ⅱ. Theoretical Framework
1. A Margin Based Asset Pricing Model
A margin based asset pricing model has been considered by Garleanu and Pedersen (2011) in a general asset pricing context. In this chapter, we describe the model briefly and discuss the relationship between margin constraint and the deviation of the Law of One Price in general setting. The application of the theoretic model on the CIP deviations will be followed in the next section.
Consider a continuous-time economy where two agents are populated with different risk
aversion γa and γb. Agent a (averse agent) has higher risk aversion than agent b (brave agent), more
averse to risk. Especially, agent a has the standard constant relative risk aversion
preferences 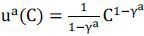 with γa>1, while agent b has log utility ub(C) = log(C) with relative risk aversion γb=1. The braver agent b can be considered as more risk-tolerant investors such as banks
or hedge funds, while the risk averse agent a can be considered as private (retail)
investor or pension fund. This economy has several risky assets with price process
given by an Ito diffusion. There are two riskless assets, one for collateralized loans
and the other for uncollateralized loans, and each asset has riskless return denoted
as
with γa>1, while agent b has log utility ub(C) = log(C) with relative risk aversion γb=1. The braver agent b can be considered as more risk-tolerant investors such as banks
or hedge funds, while the risk averse agent a can be considered as private (retail)
investor or pension fund. This economy has several risky assets with price process
given by an Ito diffusion. There are two riskless assets, one for collateralized loans
and the other for uncollateralized loans, and each asset has riskless return denoted
as 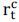 and
and 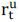 . Each security is presumed to have margin
. Each security is presumed to have margin 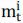 ∈[0, 1]. The margin process is also an Ito diffusion and determines the investor’s
own capital to trade the security. For example, if
∈[0, 1]. The margin process is also an Ito diffusion and determines the investor’s
own capital to trade the security. For example, if 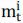 is 10% and the security price is $100, then the investor needs to pay $10 from her
capital while the remaining $90 is borrowed using the security as a collateral. In
other words, the security with $100 value is accepted as a collateral for a $90 loan,
and in this sense, the $10 difference can also be called the ‘haircut’, which is used
interchangeably with the term ‘margin’. Note that since the loan is used to finance
investment, the reciprocal of margin is the leverage that an investor can take when
trading the security. For each underlying security i, there are Ni number of derivatives ik with the same cash flows as i. Especially, the derivative ik, k=1,…, Ni pays the dividend δi.
is 10% and the security price is $100, then the investor needs to pay $10 from her
capital while the remaining $90 is borrowed using the security as a collateral. In
other words, the security with $100 value is accepted as a collateral for a $90 loan,
and in this sense, the $10 difference can also be called the ‘haircut’, which is used
interchangeably with the term ‘margin’. Note that since the loan is used to finance
investment, the reciprocal of margin is the leverage that an investor can take when
trading the security. For each underlying security i, there are Ni number of derivatives ik with the same cash flows as i. Especially, the derivative ik, k=1,…, Ni pays the dividend δi.
The equilibrium asset prices can be described by a utility maximization problem where
each agent chooses her consumption level 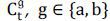 , proportion of wealth in risky assets
, proportion of wealth in risky assets 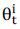 , proportion of wealth in riskless collateralized
, proportion of wealth in riskless collateralized 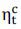 and uncollateralized loans
and uncollateralized loans 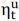 . Here we focus on the optimization problem for agent b. The logarithmic utility for
consumption implies that the agent maximizes the myopic mean-variance utility
. Here we focus on the optimization problem for agent b. The logarithmic utility for
consumption implies that the agent maximizes the myopic mean-variance utility
under the intertemporal budget constraint
and a margin constraint
Here the summation is carried out over all risky underlying securities and derivatives.
The budget constraint describes the wealth process which is determined by the investment
in risky assets, riskless assets, and consumption. The wealth after initial consumption
will gain expected returns based on her portfolio choice, but the actual increase
or decrease in the wealth will finally be determined by fundamental shocks weighted
by her portfolio. The margin constraint in (1) describes the maximum capital usage
which should be less or equal to the total wealth. Any position in risky securities
will use her own capital (or wealth) and the remainder can be invested into uncollateralized
loans, however the total capital use cannot exceed her wealth. Note that the agent’s
capital usage on a risky security i in proportion to the total wealth is 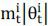 , which means that the capital is required for all trading, both long and short position.
Let us explain why the capital is required in both positions first. For a long position
, which means that the capital is required for all trading, both long and short position.
Let us explain why the capital is required in both positions first. For a long position
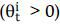 , the agent can borrow
, the agent can borrow 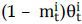 but she needs to pay the remaining portion,
but she needs to pay the remaining portion, 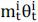 with her own capital. For a short position
with her own capital. For a short position 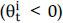 , the agent first borrows the security i and earns the purchasing value
, the agent first borrows the security i and earns the purchasing value 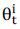 , but she must post a cash collateral
, but she must post a cash collateral  so that the net capital use is
so that the net capital use is 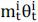 . This nonlinear margin constraint is used by Garleanu and Pedersen (2011) to capture the deviation from the Law of One Price7. They show that the margin constraint can explain the problem facing any real-world
investor.
. This nonlinear margin constraint is used by Garleanu and Pedersen (2011) to capture the deviation from the Law of One Price7. They show that the margin constraint can explain the problem facing any real-world
investor.
In addition, the risk averse investor a does not participate in the money markets
for uncollateralized loans and may be allowed in the derivatives market in limited
position. Especially, for the agent a, 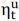 = 0 and
= 0 and 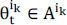 , where Aik is some admissible set of portfolio for the derivative ik. This assumption means that the uncollateralized money market may capture an inter-bank
loan market, and the risk averse agent hesitates to participate in the derivatives
market for some reasons, e.g., lack of expertise or information.
, where Aik is some admissible set of portfolio for the derivative ik. This assumption means that the uncollateralized money market may capture an inter-bank
loan market, and the risk averse agent hesitates to participate in the derivatives
market for some reasons, e.g., lack of expertise or information.
Garleanu and Pedersen (2011) show that the excess return on a risky security is determined by its margin 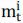 and the covariance between asset’s return and the risk tolerant agent’s consumption
growth:
and the covariance between asset’s return and the risk tolerant agent’s consumption
growth:
where 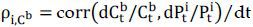 ,
, 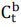 is the consumption of risk tolerant agent,
is the consumption of risk tolerant agent, 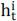 is 1 if the risk tolerant agent b is long security, −1 if she is short, and in [−1,1]
if she has no position, and ψt is the risk tolerant agent’s shadow cost of funding. Note that the shadow cost of
funding is the Lagrange multiplier attached to the margin constraint in (1). Equation
(2) shows that the excess return is decomposed into two components; the covariance
between returns and consumption growth, and the shadow cost of capital. The first
component is a standard consumption risk premium which is well characterized by the
covariance and the risk tolerant agent’s aversion to risk. The second component is
the margin premium which arises only when the margin constraint of the risk tolerant
agent is binding. In this case, the shadow cost of capital is nonzero and the agent
requires additional premium in order to trade the security. The margin premium is
given by the product of the shadow cost of capital (ψt) and margin requirement (
is 1 if the risk tolerant agent b is long security, −1 if she is short, and in [−1,1]
if she has no position, and ψt is the risk tolerant agent’s shadow cost of funding. Note that the shadow cost of
funding is the Lagrange multiplier attached to the margin constraint in (1). Equation
(2) shows that the excess return is decomposed into two components; the covariance
between returns and consumption growth, and the shadow cost of capital. The first
component is a standard consumption risk premium which is well characterized by the
covariance and the risk tolerant agent’s aversion to risk. The second component is
the margin premium which arises only when the margin constraint of the risk tolerant
agent is binding. In this case, the shadow cost of capital is nonzero and the agent
requires additional premium in order to trade the security. The margin premium is
given by the product of the shadow cost of capital (ψt) and margin requirement (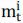 ). For example, if the margin is 10% and the shadow cost of capital is 10%, then the
additional premium required from the funding constraint is 0.1×0.1=0.01= 1%.
). For example, if the margin is 10% and the shadow cost of capital is 10%, then the
additional premium required from the funding constraint is 0.1×0.1=0.01= 1%.
Since the shadow cost of capital is a Lagrange multiplier to the margin constraint, the first order condition with respect to ηu will give the equilibrium shadow cost of capital
Consider an underlying security i and a derivative ik which have the same cash flow δi and possibly the same return volatility, while the margin on these assets differ
from each other, so that 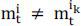 . When the margin constrains are binding, the Law of One Price violates, and they
will have different prices even if their cash flows are identical. Especially, from
the above asset pricing equation, the basis (or the difference of expected returns)
is given by
. When the margin constrains are binding, the Law of One Price violates, and they
will have different prices even if their cash flows are identical. Especially, from
the above asset pricing equation, the basis (or the difference of expected returns)
is given by
where ht = 1 or −1 if the agent b is long or short, respectively. If the risk tolerant agent
is long both assets, then the basis is given by 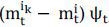 , while if long the underlying security and short the derivative, then the basis is
, while if long the underlying security and short the derivative, then the basis is
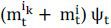 . Therefore, depending on the position of the risk tolerant agent, the basis may be
reduced or magnified.
. Therefore, depending on the position of the risk tolerant agent, the basis may be
reduced or magnified.
The consumption risk premium is vanished because the return volatility of the underlying security is assumed to be identical to the derivative. However, if they differ, then the basis is given by
This equation implies that when the return volatility of both assets differs, or equivalently, the covariances between the risk tolerant agent’s consumption and those securities are relatively distinct, the basis does not disappear even if the margin constraints are not binding.
2. Testable Implication on the CIP Deviation
Let st be the spot rate for KRW/USD at time t, ft the forward rate, 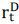 the interest rate in Korea, and
the interest rate in Korea, and 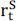 the interest rate in the US. The exchange rates are in units of Korean won per unit
of US dollar. Under the CIP relation, the US dollar rate
the interest rate in the US. The exchange rates are in units of Korean won per unit
of US dollar. Under the CIP relation, the US dollar rate 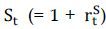 should be equal to the implied dollar rate which is the return from an investment
by converting a unit of US dollar into Korean won by spot rate, receiving the interest
from Korea, and re-converting the Korean currency into US dollar by forward rate.
Especially, the implied dollar rate Dt is calculated by
should be equal to the implied dollar rate which is the return from an investment
by converting a unit of US dollar into Korean won by spot rate, receiving the interest
from Korea, and re-converting the Korean currency into US dollar by forward rate.
Especially, the implied dollar rate Dt is calculated by
If the relationship holds, then we have the CIP given by
We define the realized basis yt as the difference between implied dollar rate and the actual US dollar rate, i.e.,
yt = Dt − St.
In fact, the basis yt can be considered as a spread between the rate of return on the underlying US dollar loan (S) and on the derivative (D), which is the KRW/USD FX swap trade involving an investment into Korean won denominated loan. Especially, we can write
where 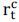 is the riskless rate of return on the collateralized loan. From the equilibrium asset
prices under binding margin constraints of the risk tolerant agent in (2), the basis
yt will have the expected return given by
is the riskless rate of return on the collateralized loan. From the equilibrium asset
prices under binding margin constraints of the risk tolerant agent in (2), the basis
yt will have the expected return given by
where 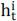 is equal to 1 if the risk tolerant agent is long the asset i, and −1 if she is short.
is equal to 1 if the risk tolerant agent is long the asset i, and −1 if she is short.
Interestingly, we observe that 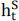 becomes 1 regardless of the agent’s position on the asset S (or the US dollar loan).
This is because we choose the interest rate for the US dollar to equal to the uncollateralized
loan rate, especially the US libor rate. More specifically, suppose that the rate
of return on S is equal to the uncollateralized loan rate, so that
becomes 1 regardless of the agent’s position on the asset S (or the US dollar loan).
This is because we choose the interest rate for the US dollar to equal to the uncollateralized
loan rate, especially the US libor rate. More specifically, suppose that the rate
of return on S is equal to the uncollateralized loan rate, so that 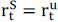 . In this case, the expected excess return on
. In this case, the expected excess return on 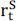 is given by ψt; the shadow cost of capital. If we remind the equilibrium asset returns under the
binding margin constraint of the risk tolerant agent,
is given by ψt; the shadow cost of capital. If we remind the equilibrium asset returns under the
binding margin constraint of the risk tolerant agent, 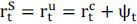 . The reason why
. The reason why 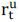 has positive premium over
has positive premium over 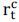 is because one unit of capital in the uncollateralized loan will have constant positive
utility with ψt, while the same unit of capital in risky assets will have different utility value
depending on the position8. This means that the uncollateralized loan rate should be greater than the collateralized
loan rate regardless of the agent’s position in the uncollateralized loan.
is because one unit of capital in the uncollateralized loan will have constant positive
utility with ψt, while the same unit of capital in risky assets will have different utility value
depending on the position8. This means that the uncollateralized loan rate should be greater than the collateralized
loan rate regardless of the agent’s position in the uncollateralized loan.
For the position on the implied dollar D, it is possible that 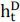 is equal to 1 or −1 depending on whether the risk tolerant agent is long or short
D. However, we assume
is equal to 1 or −1 depending on whether the risk tolerant agent is long or short
D. However, we assume 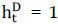 in our following estimation procedure. Here is the rationale. As we will show in
the next section (see Figure 1 for detail), it is apparent that the US dollar basis is positive on all the observations
in our sample period and the short position (or
in our following estimation procedure. Here is the rationale. As we will show in
the next section (see Figure 1 for detail), it is apparent that the US dollar basis is positive on all the observations
in our sample period and the short position (or 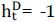 ) will imply a negative basis given the positive shadow cost of capital, which is
not evident from the data. Therefore, we set
) will imply a negative basis given the positive shadow cost of capital, which is
not evident from the data. Therefore, we set 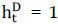 and
and 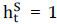 , which means that the arbitrageurs are long in the derivative (or KRW/USD FX swap)
D, while either short or long in the underlying US libor loan S. Reminding that the
US dollar rate is set to be the riskless uncollateralized loan rate, the expected
value for the realized basis (yt) is given by
, which means that the arbitrageurs are long in the derivative (or KRW/USD FX swap)
D, while either short or long in the underlying US libor loan S. Reminding that the
US dollar rate is set to be the riskless uncollateralized loan rate, the expected
value for the realized basis (yt) is given by
[Figure 1]
US Dollar Basis and TED Spread
Note: The figure presents US dollar basis and the TED spread from Jan 3, 2007 to April
16, 2010. The realized US dollar basis yt is calculated by yt = st/ft(1 + 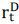 )−(1+
)−(1+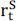 ), where
), where 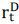 is the three month Korean CD rates,
is the three month Korean CD rates, 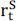 is three month US libor rates, st is the spot exchange rate, and ft is the forward rates. The TED spread is the spread between three month US libor and
three month Treasury bill rates.
is three month US libor rates, st is the spot exchange rate, and ft is the forward rates. The TED spread is the spread between three month US libor and
three month Treasury bill rates.
Additionally, we slightly modify the original model of Garleanu and Pedersen (2011) who assume that the capital usage on the uncollateralized interbank loan is 100% of the value that she decided to allocate to. This modification will allow positive basis when we use the US libor rate in calculating both the US dollar basis and the shadow cost of capital9. Especially, the modified margin constraints that we use to estimate the margin based asset pricing model is
where 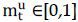 is the proportion of the value in the uncollateralized loan which will be deducted
or deposited after the choice ηu. This modification implies that the uncollateralized loan also admits funded trading
and the risk tolerant agent does not require to post 100% capital in order to long
or short the interbank loan. In essence, the weight to the uncollateralized loan
is the proportion of the value in the uncollateralized loan which will be deducted
or deposited after the choice ηu. This modification implies that the uncollateralized loan also admits funded trading
and the risk tolerant agent does not require to post 100% capital in order to long
or short the interbank loan. In essence, the weight to the uncollateralized loan 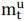 is different to the margin requirements to the risky assets i in the sense that shorting
the uncollateralized loan by
is different to the margin requirements to the risky assets i in the sense that shorting
the uncollateralized loan by 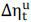 will release the risk tolerant agent’s capital by
will release the risk tolerant agent’s capital by 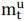 , however shorting the risky asset i by
, however shorting the risky asset i by 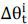 will cost her capital by
will cost her capital by 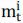 . Nonetheless, for convenience, we call
. Nonetheless, for convenience, we call 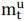 as the margin on the uncollateralized loan.
as the margin on the uncollateralized loan.
In this case, if we define the modified shadow cost of capital as
then we can find that the expected value for the realized dollar basis (yt) is given by
As we can see, the realized dollar basis (or the CIP deviation) can be explained by
the shadow cost of capital, relative margin differences, and the consumption risk
premium. The relative margin differences can capture the relative funding conditions
of Korean currency compared to the US libor loan. For example, if the funding condition
of the implied dollar loan is deteriorated, or equivalently, 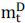 increases, the realized dollar basis is expected to increase. Also, we can expect
that the increase of the CIP deviations can also be affected by the increase of the
shadow cost of capital or the increase of the volatility on the implied dollar loan.
In the next section, we describe the econometric methodology where the relative margin
differences are assumed to be a nonlinear logistic function of an unobservable latent
factor.
increases, the realized dollar basis is expected to increase. Also, we can expect
that the increase of the CIP deviations can also be affected by the increase of the
shadow cost of capital or the increase of the volatility on the implied dollar loan.
In the next section, we describe the econometric methodology where the relative margin
differences are assumed to be a nonlinear logistic function of an unobservable latent
factor.
Ⅲ. Econometric Methodology
1. Discrete Approximation to the Continuous-time Asset Pricing Equation
Here we explain how to specify and estimate the model for the realized basis in the CIP relations. We set the margin condition as time-varying and a nonlinear function of unobservable (or latent) state variable. As noted before, the funding conditions (or the margin requirements) are not directly observable in the FX swap market, and moreover, they seem to be dependent on the market conditions, such as market illiquidity; see Brunnermeier and Pedersen (2008) for example. The logistic form of nonlinearity is used to restrict the margin requirements to be in an admissible range and to model the nonlinear variations in the funding conditions depending on the state variables. In what follows, we describe our empirical methodology to identify the parameters, and to make an inference for testable implications on the realized dollar basis (yt) and the funding liquidity condition.
Now, we consider the return processes of the US dollar uncollateralized loan S and its derivative D given by Ito diffusions as
and
where 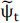 is the Lagrange multiplier of our modified model in (3). For simplicity, we assume
that there is no dividend10 for asset S and D. The difference of these two return processes is given by
is the Lagrange multiplier of our modified model in (3). For simplicity, we assume
that there is no dividend10 for asset S and D. The difference of these two return processes is given by
where ψt is the Lagrange multipler in the original problem.
Over an interval [tj−1, tj], the realized basis process (yt)can be represented as follows:
where 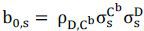 ,
, 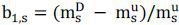 . The left hand side is the realized basis in the interval [tj−1, tj], and the first term in the right hand side is time-varying consumption risk premium,
the second term margin premium, and the last term is considered to be the disturbances
in general. If the time interval ∆= tj − tj−1 is relatively small, we can approximate the above continuous-time model into a usual
discrete-time counterpart. Especially, we can consider a usual time-varying parameter
model given by
. The left hand side is the realized basis in the interval [tj−1, tj], and the first term in the right hand side is time-varying consumption risk premium,
the second term margin premium, and the last term is considered to be the disturbances
in general. If the time interval ∆= tj − tj−1 is relatively small, we can approximate the above continuous-time model into a usual
discrete-time counterpart. Especially, we can consider a usual time-varying parameter
model given by
where β0,j = ∆b0tj−1, β1,j = ∆b1tj−1, and ψj = ψtj−1. For the brevity of notations, we will use the usual discrete time index t instead of j in what follows.
2. Nonlinear State Space Model in a Logistic Form
It is clear that the parameter β1,t should be in an admissible range because the margin requirement 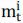 should be in the interval [0, 1]. Especially, the parameter β1,t is a bounded function of relative difference in the funding conditions, which is
not observable and possibly depends on the economic states nonlinearly11. A nonlinear transformation of the underlying latent state variable based on a logistic
function can deal with the boundedness and nonlinearity. Moreover, the parameter β0,t represents the consumption risk of the risk tolerant agent whose consumption process
should be in the interval [0, 1]. Especially, the parameter β1,t is a bounded function of relative difference in the funding conditions, which is
not observable and possibly depends on the economic states nonlinearly11. A nonlinear transformation of the underlying latent state variable based on a logistic
function can deal with the boundedness and nonlinearity. Moreover, the parameter β0,t represents the consumption risk of the risk tolerant agent whose consumption process
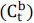 is also not observable in general. Therefore, a nonlinear state-space model approach
for the realized basis process is relevant for the estimation of the parameters.
is also not observable in general. Therefore, a nonlinear state-space model approach
for the realized basis process is relevant for the estimation of the parameters.
Specifically, we consider a nonlinear state space model in a logistic form of nonlinearity:
where β1(∙) is the relative margin function which is determined by a latent state variable in the following fashion
with ν> 0. In this model, β0,t can be interpreted as time-varying consumption risk premium and β1(∙) is the relative difference in margin condition which is a nonlinear function of the state variable (w1,t). The logistic function can capture the nonlinearity of the relative margin difference with respect to the latent state variable w1,t, and at the same time, β1(∙) is restricted to be in the interval [−1, −1 + v]12. Depending on the value of v, the relative margin difference will have the upper bound −1 + v.
In order to deal with the nonlinearity, we follow the approach by Kim and Nelson (2006). Especially, the nonlinearity of β1(∙) is tackled down by local linearization based on the Taylor expansion around the predicted value of w1,t based on previous information. The above state space model can be reformulated as
where
For the estimation of the parameters, we simply apply the standard Kalman filter approach. Using the Kalman filter, we can extract the time-varying consumption risk premium β0,t, and the relative difference in the funding condition β1(w1,t).
IV. Empirical Analysis
1. Data
In order to measure the realized US dollar basis, we use three month libor rate for the US interest rate and the yield for three month CD for the Korean interest rate. The three month rates are in annum so we first adjust the rates for three-month period by multiplying 91/360 to the rates, and convert the resulting dollar rates into annum. The US libor rate is obtained from Bloomberg, and the CD rates are from the Korea Financial Investment Association. In order to calculate the forward rate, we use a series of swap point data, which is often used to quote the FX swap trade. Especially, our forward rate is obtained by the summation of the spot rate and swap point. All data for the spot rate and swap point are observed at 16:00 in New York time and the source is Bloomberg.
We exploit the shadow cost of capital to extract the relative difference in the margin condition using the nonlinear state space model. The empirical measure for the shadow cost of capital is based on the interest rate spread between uncollateralized and collateralized loan, which is determined by the margin based asset pricing model of Garleanu and Pedersen (2011). As discussed earlier, we use three month US libor rate as a proxy for the uncollateralized loan rate and three month Treasury bill rate for the collateralized loan rate13. This spread is often called the TED spread, which measures the shadow cost of capital in bad times when the margin constraints are binding.
2. CIP Deviation and Relative Margin
In this section, we present the empirical findings regarding the CIP deviations and estimation results for the margin based asset pricing model based on our nonlinear state space model.
Table 1 presents the summary statistics of Korean, US interest rates, spot and forward exchange rates of KRW/USD from Jan 1, 2007 to Apr 16, 2010. As we can see, all the variables show high persistence for the whole period with autocorrelation coefficients exceeding 0.9. This is a well expected feature of the interest rates and exchange rate data. Interestingly, if we compare the samples from pre and post Lehman bankruptcy, we can see that the persistency has been increased for all the variables. Similarly, the realized US dollar basis (or the deviation from the CIP) has been increased during the recent financial crisis, especially after the Lehman bankruptcy. The mean level has jumped from 1.52% to 2.96%, and so does the standard deviation of the basis. The proxy for the shadow cost of capital (or the TED spread) seems to be decreasing in its mean level from 0.96 to 0.83 after the Lehman bankruptcy. Figure 1 presents the realized US dollar basis and the TED spread for our sample period. It is quite apparent that the TED spread and basis move very closely for the period from January 2007 to November 2008, however after the Lehman bankruptcy the co-movement looks to be very weak and dying out. This might imply that the contribution from the funding liquidity premium is getting smaller after the bankruptcy, meanwhile other factors, such as the consumption risk or default risk contributed more in explaining the dollar basis.
<Table 1>
Summary Statistics
Note: Summary statistics for Korean three month CD rates (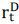 ), US three month libor rate (
), US three month libor rate (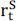 ), spot KRW/USD exchange rates (st), forward exchange rates (ft), implied dollar rates (Dt = st/ft(1 +
), spot KRW/USD exchange rates (st), forward exchange rates (ft), implied dollar rates (Dt = st/ft(1 + 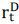 )), dollar rates (St = 1 +
)), dollar rates (St = 1 + 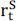 ), the dollar basis yt = (Dt − St), and the shadow cost of capital (ψt). The shadow cost of capital is three month TED spread. All the interest rates are
in percentage units, and the exchange rates are in units of Korean won per unit of
US dollar.
), the dollar basis yt = (Dt − St), and the shadow cost of capital (ψt). The shadow cost of capital is three month TED spread. All the interest rates are
in percentage units, and the exchange rates are in units of Korean won per unit of
US dollar.
Table 2 presents the estimation result for our nonlinear state space model in a logistic form. All the parameters are estimated to be significant. The volatility of the disturbances is estimated to be 0.053 while the volatilities for the latent factors are estimated to be 0.108 and 0.190, respectively. The volatility of the margin premium is considered to be much larger compared to the volatility for the consumption risk premium because the relative margin differences are set to be a nonlinear function of more volatile latent factor (w1,t). The upper bound v is estimated to be 8.655, implying that the margin on the implied loan can be about 10 times higher than the margin on the US libor loan in an extreme case. This means that the investor’s own capital can cost up-to 10 times more when taking positions in the implied dollar loan compared to the US libor loan.
<Table 2>
Estimation Result of the Nonlinear State Space Model
Note: The table presents the estimation results of the nonlinear state space model in Section 3. 1.
Figure 2 shows the extracted relative difference in margins based on our nonlinear state space model. The relative margin difference can be interpreted as the relative difference in funding liquidity (or tightness in funding liquidity) in KRW/USD FX swap market compared to the US libor market. Since the margins are the reciprocal of the leverage that an investor can take in funding the position of a risky asset, higher margins imply lower leverages and vice versa. This implies that higher margin securities are, in general, harder to fund than lower margin securities.
[Figure 2]
Relative Margin Differences
Note: The figure presents the relative difference in margin conditions (mD−mS)/ mS based on our nonlinear state space model and its 95% confidence bands (based on delta-method). The extracted relative margin differences are from May 31, 2007 to April 16, 2010.
As we can see, the relative differences in margins are positive for most of our sample period. This implies that the funding condition of the FX swap market in Korea is, in general, poorer than the US libor market. Considering the uncertainties regarding the macroeconomic prudence of Korea, especially the foreign currency liquidity problem during the global financial crisis, the upper bound of leverages that international investors can take for the long position in the Korean won could be restricted and make the margin on the implied dollar loan stay at a higher level than the US libor. Moreover, we find evidence that the increase in the relative margin differences has magnified the increase in the deviation from the covered interest parity. The CIP deviation, as we discussed earlier, is determined by the relative margin differences, the shadow cost of capital, and the consumption risk premium. If we look at the period from the Lehman bankruptcy to the early October 2008, both the relative margin differences and the shadow cost of capital spiked up, resulting in the soar of the CIP deviations. We also can check from Figure 2 that the relative margin differences are more significant during the period when the CIP deviations soared. This implies that the increase of the CIP deviations are largely driven by the increase of the shadow cost of capital, and the relative margin differences have a magnifying effect of further increasing the deviation. Also, we observe that the relative margin differences can quickly explode to a very high level and solely affect the CIP deviation. If we focus on the period from the early October 2008 to the early December 2008, the relative margin differences boosted up to the highest level of 3.9 while the shadow cost of capital decreased significantly to the pre-Lehman level. In this period, the CIP deviations recorded the highest level of 1,000bp. The reason why the CIP deviations increased further even if the shadow cost of capital is decreased is because the relative margin differences have shot up very quickly. It seems that the funding condition in the implied dollar loan has deteriorated while the funding condition in the US libor loan has improved, so that the relative margin differences have quickly increased and contributed to the skyrocketing CIP deviations. The improved funding liquidity in the US libor loan and the decrease of the shadow cost of capital might be affected by the large swap line between central banks, especially between Federal Reserve and European Central Banks in the mid-September 2008. Meanwhile, the funding condition in the implied dollar loan is disturbed by the concern on the foreign currency liquidity crisis of the financial institutions in Korea. As the gap between the implied dollar and US libor funding conditions widened, the CIP deviations have further increased and recorded the highest level. In the mean time, the $30 billion swap line between Federal Reserve and the Bank of Korea (BOK) has been set at the end of October 2008. A month later, the relative margin differences dropped, and as a result, the CIP deviations also came down to the pre-Lehman level.
The swap lines between Federal Reserve and the central banks of developing countries have positively affected the decrease of both the shadow cost of capital and the margin on the US libor loan, while the swap line between Federal Reserve and BOK seems to attenuate the margin on the implied dollar loan. Since the margin on the implied dollar loan reflects the credit worthiness and/or the liquidity on the Korean government bond, lowered margin implies that the government bond has regained its market confidence (or the collateral value has improved). As Baba and Shim (2010) noted, the swap line effectively increase the BOK’s foreign reserves, which should have enhanced market confidence, leading to the decrease of margin on the implied dollar loan. However, it seems that the time-lag between the swap lines may affect the funding conditions differently, amplify the relative margin, and increase the CIP deviations further. Note that after December 2008, the relative margin differences are no longer significant in explaining the variations of the CIP deviations. This implies that the shadow cost of capital disappears in the pricing of the price deviations and the funding liquidity crisis might pass away.
We also find that the consumption risk premium also explains the CIP deviations. Figure 3 presents the margin premium and consumption risk premium imposed in the CIP deviations. The margin premium is calculated by multiplying the relative margin differences to the shadow cost of capital. As we can see, the consumption risk premium is relatively stable compared to the margin premium. Assuming that the consumption volatility itself is relatively small, the consumption risk premium is basically determined by the volatility of the implied dollar loan (or the swap point). As expected, the consumption risk premium increased after the Lehman bankruptcy and stayed around 2% level until the mid 2009. Since the margin premium is not significant after December 2008, it seems that the decrease in the CIP deviations after December 2008 is largely affected by the stabilization of the volatility in the FX swap market. In this regard, it is clear that when the FX swap market is stable and the liquidity concern is no longer binding, the CIP deviations will be much decreased.
[Figure 3]
Margin Premium vs. Risk Premium
Note: The figure presents the margin premium and consumption risk premium imposed in the US dollar basis. Both the margin and risk premium are extracted by the nonlinear state space model. Especially, the figure plots β1(w1,t)TEDt and β0,t for the margin and risk premium, respectively.
In sum, we find that the shadow cost of capital together with relative margin differences can explain the deviation from CIP in the sample period before December 2008. From our analysis, it was evident that the relative margin differences can magnify the increase of the CIP deviation in the liquidity crisis period. Moreover, the relative margin differences can quickly increase to the very high level and affect solely to the increase of the CIP deviations when the funding liquidity in the global money market improved with some time-lag. Also, it seems that the central bank swap line between Federal Reserve and the Bank of Korea help to improve the funding condition for the implied dollar loan, and finally decrease the CIP deviation. After the liquidity crisis period, the stabilization of the FX market seems to be important in decreasing the CIP deviations.
3. Does Market Illiquidity Affect Margin?
Now we turn our attention to the question whether market illiquidity affects the relative margin differences. As Brunnermeier and Pedersen (2008) argued, the margin spiral can emerge if the market illiquidity can disturb the funding condition (or increase the margin on the security). In this case, the margin spiral can emerge so that the margins have magnifying effect in increasing the financial instability. In order to investigate the relationship between the margins and the market illiquidity, we consider overnight MBS-Treasury repo spread as an empirical proxy for the market illiquidity. Recently, Coffey et al. (2009) suggest using the overnight MBS-Treasury repo spread as an empirical proxy for relative market illiquidity of the two repo securities. As discussed in their paper, repo markets have become one of the main sources of funding for commercial banks, investment banks and securities lenders in recent years. Therefore, the relative illiquidity of MBS repo to the Treasury repo is assumed to be general collateralized loan market illiquidity in the sense that the illiquidity in the repo market will affect the trading activities of the banks, leading to the money market illiquidity. Also, the relative margin differences may be affected by the credit risks of the Korean government bond because the margin on the implied dollar loan should reflect the credit worthiness of the government bond. When the credit risk is high, then overall expected risk compensation is increasing so that the asset prices including the collateral value will fall. This can affect the margin on the implied loan.
We use three month MBS-Treasury spread, which are the spread between three month repo rate using MBS as collateral and three month repo rate using Treasury bill as collateral. We also use the CDS spread of the 5 year dollar denominated government bond of Korea for the credit risk. All the data is provided by Bloomberg.
Table 3 presents a simple regression result of the relative margin differences being regressed on our proxies for the market illiquidity and credit risks for the sample period from May 31, 2007 to December 31, 2008 when the funding liquidity concerns seem to affect the CIP deviations. Note that the extracted relative margins are available from May 31, 2007 because we discard the first 100 observations for estimating the nonlinear state space model. As we can see from the table, all the regression coefficients are significant and positive. This suggests that both the market illiquidity and credit risks increase the relative margin differences. We also can check from Figure 4 that the overall variations of the relative margin differences are well captured by the market illiquidity and the credit risks.
<Table 3>
Market Liquidity and Relative Margins
Note: The table represents a simple regression results of yt = xtβ + ut, where yt is the relative margin differences and xt is a collection of explanatory variables, especially the market illiquidity (MBS-Repo spread), counterparty risk (CDS premium) and a constant term. The sample period is from May 31, 2007 to Dec 31, 2008, and the number of samples in this period is 683.
[Figure 4]
Fitted Relative Margin Differences
Note: The figure presents relative margin (mD−mS) / mS and market illiquidity. We use three month MBS-Treasury repo spread as a proxy for the market illiquidity and CDS spread for 5-year government bond of Korea for the credit risks. For the estimation of relative margin, we use the nonlinear state space model. Note that the starting date is May 31, 2007 because we discard the first 100 estimates.
V. Conclusion
There has been lasting question on why the deviation of covered interest rate parity in KRW/USD FX market has lasted long and wide, especially during the global financial crisis. In order to answer the question, we use the framework of Garleanu and Pedersen (2011) who relates the funding constraint and deviations of the Law of One Price. According to their result, the margin constraint has an important role in equilibrium asset prices and the Law of One Price will be violated under the binding margin constraint of the risk tolerant agent. When the fundamental is bad, the margin requirements are binding so that the arbitrageurs cannot borrow from the risk averse agents as they wanted and this will decrease the collateralized loan rate (or riskless interest rates, or Treasury rates) in order to induce the risk averse agents not to lend as much they would like to. Also, the uncollateralized loan rate (or interbank loan rates) will be greater than the collateralized loan rate to reflect the shadow cost of capital of the risk tolerant agent. The shadow cost of capital, which is close to zero in normal times, will spike up in the financial turmoil and affect the asset prices with identical cash flows but different margins. In the context of CIP deviations, the different margin requirements (or haircuts) of US libor loan and implied dollar loan induced from FX swap trade will contribute to the increase in the CIP deviations.
Our estimation results show that the margin difference together with the shadow cost of capital is the main cause of the CIP deviations. With our empirical analysis for the CIP deviations, we extract the relative margin differences and find that the shadow cost of capital together with relative margin differences can explain the deviation from CIP in the sample period before December 2008. From our analysis, it was evident that the relative margin differences can magnify the increase of the CIP deviation in the liquidity crisis period. Moreover, the relative margin differences can quickly increase to the very high level and solely affect to the increase of the CIP deviations when the funding liquidity in the global money market improved with some time-lag. Also, it seems that the central bank swap line between Federal Reserve and the Bank of Korea help to improve the funding condition for the implied dollar loan, and finally decrease the CIP deviation. After the liquidity crisis period, the stabilization of the FX market seems to be important in decreasing the CIP deviations.
Another contribution of our paper is that we provide an empirical evidence for the relationship between the relative margins and market illiquidity. In a recent work by Brunnermeier and Pedersen (2008) on the margin and funding constraints, lower market liquidity may increase margins, which tightens investor’s funding condition further, leading to the so-called margin spiral. Such a feedback effect has been considered based on the assumption that the market illiquidity is increasing the margin requirements, and we show an evidence that the market illiquidity can increase the margins. We also believe that the margin and funding liquidity channel which derives the CIP deviations can be compared to other interesting theoretical models with alternative model specification. We leave these tasks to future works.
Notes
본 논문은 기 발간된 Margin and Funding Liquidity: An Empirical Analysis on the Covered Interest Parity in Korea(Policy Study, 2010-01, 한국개발연구원, 2010)을 보완 및 수정한 것임을 밝힌다.
In our paper, the margin is the difference between the collateral value and the face value of a security. Therefore, higher margin can be understood as tighter funding condition because one can fund smaller portion of the face value. Please refer to the Section II. 1. about the formal definition of the margin.
FX swap counterparties in most cases establish a mutually agreed upon margin threshold. The threshold is determined on each swap contracts based on the credit ratings of individual parties. For detailed illustration on the FX swap margin threshold, refer to Barku and Ong (2010).
Formally we define the return on the implied dollar loan (D) as the return from an investment by converting a unit of US dollar into Korean won by spot rate, receiving the interest from Korea, and reconverting the Korean won into US dollar by forward rate, i.e., D = s/ f(1 + rD), where s spot, f forward rates in unit of Korean Won per unit of US dollar, and rD is the interest rate for Korean won.
A repurchase agreement (repo) is the sale of a security with a commitment by the seller to buy the same security back from the purchaser at a specified price at some future date. Therefore, the security buyer provides a collateralized loan to the security seller. A reverse repo is viewed from the perspective of the counterparty lending cash.
The amount by which the market value of the security used as collateral (face value) exceeds the value of the loan (collateral value) is called the repo margin.
The CIP deviations are defined as the spread between implied dollar rate (D) and spot dollar rate (S = (1 + rs) with rs being US interest rate) , i.e., CIP deviation.= D − S.
Garleanu and Pedersen (2008) show that the deviation of the Law of One Price cannot
arise in the linear margin constraint given by 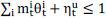
While the utility value for the position of a risky asset i will be 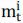 ψt if she is long i and −
ψt if she is long i and −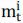 ψt if she is short, the utility value for the position of a riskless uncollateralized
loan is ψt, regardless of the position.
ψt if she is short, the utility value for the position of a riskless uncollateralized
loan is ψt, regardless of the position.
A simple application of the asset pricing equation (2) will show that under no consumption
risks, the US dollar basis can be written as 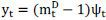 where
where 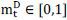 . In this case, the theoretical basis should be always less or equal to zero.
. In this case, the theoretical basis should be always less or equal to zero.
This assumption is equivalent to the setting where the dividend process for i and ik are identical.
Since the margin requirements are positive and cannot exceed 1, the relative margin
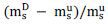 should be in the range of [−1, +∞).
should be in the range of [−1, +∞).
The lower bound for β1(∙) is determined by the lower bound of the relative margin difference 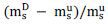 multiplied by the time interval ∆. Typically, the time interval for daily observations
is set to be 1/250, but we set ∆= 1 because we use annualized dollar basis in our
empirical analysis.
multiplied by the time interval ∆. Typically, the time interval for daily observations
is set to be 1/250, but we set ∆= 1 because we use annualized dollar basis in our
empirical analysis.
Coffey et al. (2009) also use the three month Treasury bill rate as a proxy of the collateralized loan rate.
References
(1973). The Interest Rate Parity Theorem: A Reinterpretation. Journal of Political Economy, 81, 1451-1459, https://doi.org/10.1086/260137.
, & (2009). Interpreting Deviations from Covered Interest Parity during the Financial Market Turmoil of 2007-08. Journal of Banking & Finance, 33, 1953-1962, https://doi.org/10.1016/j.jbankfin.2009.05.007.
, & (1977). Transaction Costs and Interest Arbitrage: Tranquil Versus Turbulent Periods. Journal of Political Economy, 85, 1209-1226, https://doi.org/10.1086/260633.
, & (2011). Margin-based Asset Pricing and Deviations from the Law of One Price. The Review of Financial Studies, 24, 1980-2022, https://doi.org/10.1093/rfs/hhr027.
, , & (1992). Unobserved Component Time Series Models with Arch Disturbances. Journal of Econometrics, 52, 129-157, https://doi.org/10.1016/0304-4076(92)90068-3.
, & (2006). Estimation of a Forward-looking Monetary Policy Rule: A Time-varying Parameter Model Using ex Post Data. Journal of Monetary Economics, 53(8), 1949-1966, https://doi.org/10.1016/j.jmoneco.2005.10.017.