
- P-ISSN 1738-656X

We study incentive structures of public developers and land owners in the process of public expropriations using a sequential game model. In the model, we show that there is an incentive for the public developer to give more compensation than just compensation that are defined by law. Also the model shows that there is an incentive for the land owners to revolt strategically against the public expropriation.
Then an ideal authority delegation model is introduced to resolve the problems, where an independent appraiser determines the compensation for the expropriation. In the real world, improving the independence of appraisal process is critical to make the system closer to the ideal authority delegation model. So this paper concludes by making a few policy suggestions to improve the current appraisal system.
공공수용, 정당보상, 권한위임, 감정평가, Public Expropriation, Just Compensation, Authority Delegation, Appraisal
K11, C78, D82, R14
「헌법」에서 정하는 바에 따르면, 공공의 필요에 의하여 사업을 추진함에 있어서 부득이한 경우 법률이 정하는 바에 따라 정당한 보상을 지급하여 민간의 토지(재산)를 수용할 수 있다.1) 이때 「헌법」에서 명시하고 있는 정당한 보상에 대한 기준, 특히 보상절차나 보상액에 대한 기준에 대해 해당 토지소유자나 일반 국민들의 동의를 얻지 못한다면 사회적인 갈등과 분쟁을 야기할 수 있다. 공공수용에 따른 보상액을 토지소유자가 기대하는 정도에 비해 너무 적게 책정한다면 재산권을 침해당한 토지소유자의 강한 반발을 사게 된다. 또한 수용을 통한 공공사업 추진계획에 대해 일반 국민들에게 제대로 알리고 동의를 구하지 않거나, 사업을 추진하는 과정에서 과다한 보상액 책정으로 예산을 낭비하게 되면 납세자인 국민들의 강한 반발을 사게 된다.
이러한 갈등의 소지를 줄이기 위해 「공익사업을위한토지등의취득및보상에관한법률」을 비롯한 관련 법령에서 공공용지에 대한 매수, 수용 및 손실보상에 관하여 절차와 기준을 마련하고 있다. 이는 국민의 재산권을 보호하고 동시에 공공사업의 원활한 추진을 도모하기 위한 것이다.
하지만 공공수용과 관련한 개별 사례들이 너무 다양하여 법적 규정의 허점을 이용한 투기 및 이와 관련한 분쟁과 갈등은 여전히 지속되고 있다. 본 연구는 이러한 분쟁과 갈등의 근본 원인을 찾아내고 개선방안을 제시하는 데 목적이 있다. 이를 위해 우선 공공수용 제도 및 절차를 게임이론모형으로 단순화시켜 공공수용과 관련한 당사자들의 유인구조와 의사 결정과정을 살펴본다. 이를 통해 어떠한 결과가 게임의 균형으로 도출되고, 만약 게임의 구조가 바뀌면 균형이 어떻게 바뀌는지 살펴보고자 한다.
본 논문에서는 우선 모형의 분석을 통해 수용자는 피수용자에게 법에서 의도하는 정당보상액보다 큰 액수의 보상액을 지급하려는 인센티브가 존재할 수 있음을 보인다. 또한 피수용자는 전략적으로 공공수용에 대하여 반발하고 갈등을 일으킬 유인이 존재할 수 있음도 보인다. 그리고 이 같은 인센티브를 차단하기 위한 이상적인 형태의 권한위임모형을 살펴본다. 여기서 이상적인 권한위임은 감정평가업무가 수용자나 피수용자의 이해관계에 영향을 받지 않을 때 도달된다. 하지만 현실에서는 이러한 이상적인 권한위임이 이루어지지 못하고 있음을 보였다. 그리고 이를 바탕으로 이상적인 형태의 권한위임에 보다 근접하기 위해서 제도적으로 개선해야 할 사항들을 살펴본다.
본고의 구성은 다음과 같다. 제Ⅱ장에서 관련 선행 연구에 대해 간략히 살펴본 후, 제Ⅲ장에서는 본 연구의 기본모형을 제시한다. 공공수용절차와 관련하여 우선 법에서 정하고 있는 정당보상액 수준에 대해서 살펴본 후 수용자와 피수용자의 최적 선택으로부터 도출되는 보상액 수준이 정당보상액 수준과 차이가 날 수 있음을 보인다. 이어지는 제Ⅳ장에서는 피수용자가 공공수용에 대한 반발의 정도를 정할 수 있는 모형을 살펴보고, 이를 통해 피수용자는 전략적으로 공공수용에 대하여 반발하고 갈등을 일으킬 유인이 존재할 수 있음을 보인다. 제Ⅴ장에서는 보상액 책정과 관련한 권한을 제3자인 평가자에게 위임함으로써 정당보상을 달성하고 갈등을 줄일 수 있는 이상적인 모형을 보이고, 현재의 제도가 보다 이상적인 형태에 근접하기 위한 제도 개선방향을 모색한 후, 제Ⅵ장에서 논의를 마무리 짓는다.
토지수용과 관련하여 법학과 경제학 분야에서 선행 연구가 진행되었다. 그동안 국내 문헌에서는 주로 법학자들을 중심으로 토지수용과 관련된 정당보상에 대한 연구2)가 많이 진행되어 온 반면, 일부의 국내 문헌과 해외 문헌에서는 경제학적인 접근도 함께 시도되어 왔다.
그중에서도 Shavell(2010)과 Miceli and Segerson(2007)의 두 연구가 본 연구와 밀접한 관련이 있다. Shavell(2010)은 정부가 공공사업을 위해 토지를 수용할 때 원토지소유주와의 협상을 통하거나 토지수용권(Eminent Domain)을 사용하는 등의 두 가지 방법에 대해 모형을 세우고 토지가치에 대한 정보의 비대칭하에서 각각의 방식이 어떠한 장단점이 있는지 분석하였다. 또한 원토지소유주의 수가 소수인지 다수인지에 따라 모형의 결과가 달라짐을 보였다. Miceli and Segerson(2007)에서는 버티기 문제(holdouts)가 존재할 때 이 같은 문제가 토지수용자와 소유주 사이의 협상력에 미치는 영향에 대해서 분석하였다. 개발의 규모에 따라 버티기 문제의 심각성이 달라지고 이에 따라 두 당사자 간의 협상력이 변화됨을 보였다. 이 두 연구는 토지소유자가 협상을 지연함으로써 공공사업의 진행을 방해할 수 있다는 점을 이용하여 협상력을 강화시킬 수 있음을 보였다는 점에서 본 연구와 상당한 관련이 있다. 하지만 본 연구에서는 국내 토지수용제도의 특성을 포함하여 게임이론적인 접근을 하였다는 데 위 연구들과 차이가 있다. 특히 국내 토지수용제도에서는 공공사업자와 토지소유자 사이의 보상금 산정 관련 협상을 엄격히 제한하고 있으며, 산정된 보상금액에 대해서도 토지소유자는 받아들일지 아니면 조정의 단계를 거칠지만 결정할 뿐 위 연구들에서 가정하고 있는 추가적인 협상 등은 불가능하다. 이 같은 협상과정의 특성을 반영하여 모형을 제시하였고, 이에 따라 결론을 도출하고 있다. 즉, 국내의 제도를 바탕으로 수용보상금과 관련한 이해관계를 경제학적 모델을 바탕으로 체계적으로 분석하였다는 점에서 본 연구는 기존의 법학적·경제학적 연구들과 차별성을 가진다.
본 장에서는 토지수용과 관련한 게임 이론모형을 설정하고, 이를 통해 수용과 관련한 이해관계를 분석하여 모형에서의 균형은 어떠한지 살펴보고자 한다. 구체적으로 말해서 정부 및 공공수용자(이하 “수용자”라 한다), 잠재적으로 자신의 토지를 수용당할 수 있는 토지소유자(이하 “피수용자”라 한다), 그리고 분쟁을 최종적으로 조정하는 위원회 혹은 법원(이하 “조정자”라 한다) 등이 참여하는 순차게임을 고려한다.
수용자가 공적인 사용을 목적으로 사유지를 수용하여 개발했을 시 기대할 수 있는 사회적 가치를 S ∈ R+ 라고 정의하고, 그 가치의 크기에 대해서는 모두가 알고 있다(common knowledge)고 가정한다. 그리고 피수용자가 소유하고 있을 때의 토지가치를 확률변수 V ∈ [0, V] ⊂ R+라고 정의한다. 여기서 토지가치를 확률변수로 정의한 이유는 다음과 같다. 피수용자가 자신의 토지에 대해 가지는 가치에는 객관적으로 인정받을 수 있는 가치와 더불어 피수용자의 주관적인 가치가 함께 내재되어 있다. 따라서 피수용자의 주관적 성향에 따라 해당 토지에 대해 가지는 가치는 다양하며, 이러한 주관적 가치는 당사자만이 정확히 알 수 있다. 여기서는 피수용자가 가지는 주관적 가치에 대해서 다른 사람들이 정확히 알 수 없고 대신 그 가치의 분포에 대해서만 알 수 있다고 가정한다. 그렇게 되면 피수용자가 아닌 입장에서는 피수용자의 토지가치 V는 일정한 분포를 가진 확률변수라고 할 수 있다. 그러므로 본 모형에서는 확률변수 V의 기댓값은 모두가 정확히 알 수 있는 객관적 가치에 의해 정해지고, V의 실제값은 객관적 가치와 주관적 가치가 모두 반영되어 피수용자만이 알 수 있도록 정해진다고 가정하고 있다. 즉, 피수용자 토지의 가치 V (실현된 V값)는 수용자만 알고(private information)있으며, V의 분포(분포함수 F )에 대해서만 모두가 알고(common knowledge) 있다고 가정한다.
본 장의 제2절에서는 논의의 단순화를 위해 토지가치에는 객관적 가치만이 존재해서 수용자도 V의 정확한 값을 알고 있다고 가정하여 모형을 분석한다. 제3절에서는 토지가치에 객관적 가치와 주관적 가치가 모두 존재해서 수용자는 V의 확률분포에 대해서만 알고 있다고 가정하여 균형을 도출하고자 한다.
본격적인 논의를 위해 본 모형에서는 분포함수 F에 대하여 다음과 같은 가정을 필요로 한다.
가정 1: 분포함수 F는 연속증가함수이며 오목함수이다. 그리고 F(0) = 0이다.
F가 증가함수라는 가정의 의미를 다시 표현하자면, V값은 0을 포함한 어떠한 양의 값도 가질 수 있다는 의미이다. 그리고 오목함수라는 가정은 V의 값이 지나치게 큰 값을 가질 확률은 상대적으로 매우 낮음을 의미한다. 또한 분포함수가 연속함수이며 F(0) = 0이라는 가정은 이 분포에서 V는 특정한 값에서 양의 확률측도(probability measure)를 갖지 않는다는 의미이다.
공공수용을 통한 사업이 사회적 효율성을 확보하기 위해서는 해당 공공사업의 사회적 가치 S가 기존 토지의 가치 V에 비해서 커야 한다. 본 모형에서는 기본적으로 사회적 효율성을 확보한 공공사업의 경우를 살펴보고자 한다. 즉, 해당 사유지의 공공수용을 통해 기대할 수 있는 가치 S가 토지가치에 비해 충분히 큰 경우를 상정하고 있다.
가정 2: S > V.
본 절에서는 공공수용에 관한 구체적인 모형을 다루기에 앞서 민간이 해당 토지를 시장에서 거래할 때 어떤 식으로 거래가 이루어질 것인지 살펴본다. 그리고 이를 바탕으로 공공수용 시에 법에서 정하고 있는 정당보상액에 대해서 살펴본 후, 이를 본 모형에서는 어떻게 정의할 수 있는지도 함께 살펴본다.
특정 토지에 대해 V라는 개인 가치를 가진 토지 판매자가 있고, 그 토지에 대해 S라는 개인 가치를 가지는 토지 구매자가 있다고 하자. 토지 판매자는 V 이상의 가격이 제시되었을 때만 자신의 토지를 팔려고 할 것이다. 그리고 토지 구매자는 토지의 가격이 S 이하일 때 토지를 살 용의가 있을 것이다. 즉, 민간 사이의 정상적인 거래에서는 토지 구매자가 평가하는 토지의 가치 S가 토지 판매자가 가지는 토지가치 V보다 클 때에만 거래가 성립된다. 그리고 이때 거래가격은 S와 V 사이에서 정해진다.
구체적인 거래가격은 거래의 절차, 협상력 등에 의해 다양하게 형성될 수 있다. 만약 S와 V값에 대해서 상호 간에 모두 알고 있다면 가격결정 협상은 전형적인 내쉬 협상 게임이라고 볼 수 있다. 토지 거래를 통해 생겨나는 추가적인 이익 S − V에 대해서 판매자와 구매자 사이에 어떻게 나눠 가지는가 하는 점이 토지가격을 통해서 정해진다. 예를 들어 둘간의 협상력이 같은 경우 가격 p는 (S + V) / 2가 되고, 판매자가 모든 협상력을 가진 경우(예를 들어 판매자가 take-it-or-leave-it offer를 구매자에게 제시하는 경우)는 p = S , 구매자가 모든 협상력을 가진 경우(반대의 예로 구매자가 take-it-or-leave-it offer를 판매자에게 제시하는 경우)는 p = V가 된다.
이번에는 구매자의 가치 S에 대해서는 모두가 알고 있지만 판매자의 가치 V에 대해서는 판매자만 아는 경우를 살펴보겠다. 이때에도 역시 가격결정 협상에서 판매자와 구매자가 가지는 협상력이 가격에 큰 영향을 미치게 된다. S에 대해서 모두가 알고 있으므로 판매자가 모든 협상력을 가진 경우는 앞서의 경우처럼 p = S의 가격을 판매자가 제시하고 구매자는 이 가격을 받아들이게 된다.
이제 반대로 구매자가 모든 협상력을 가진 경우, 즉 구매자가 판매자에게 단 한 번 가격을 제시하고 이 가격을 판매자가 받아들이면 거래를 하고 그 가격을 받아들이지 않으면 거래가 이루어지지 않는 경우(take-it-or-leave-it offer가 가능한 경우)를 살펴보자. 이 경우는 뒤에서 다룰 공공수용모형과 상당히 유사한 형태를 가진다. 구매자가 제시하는 금액을 x ∈ [0, S]라고 하면 구매자의 기대이익은 다음과 같다.
위 기대이익의 일계미분조건은
이므로, 위 일계조건을 만족하는 제시액 x*가 최적 제시액이 된다.3) 위의 식 (3-2)를 다시 적어보면 다음과 같이 된다.
위 식의 좌변은 구매자가 자신의 제시액을 추가적으로 높임으로 인해 판매자가 제시액을 받아들일 가능성이 증가하면서 생겨나는 추가적인 이득을 의미한다. 그리고 우변은 구매자가 제시액을 추가적으로 높임에 따라 거래가 성사되었을 시 얻게 되는 이득이 줄어드는 정도를 의미한다. 이 둘이 같아지는 점에서 최적 제시액이 정해지는 것을 위 일계조건식 (3-2)는 보여주고 있다.
구매자가 단 한 번 가격을 제시하는 경우는 그 제시된 가격에 대해 판매자가 거절할 경우 구매자는 아무것도 얻지 못하므로, 예상되는 판매자의 가치 V가 높을수록, 즉 구매자의 제시액에 대해서 거절할 가능성이 높을수록 구매자의 최적 제시액은 높아진다. 그리고 판매자가 거절할 가능성이 극단적으로 높은 경우 (F(S)의 값이 매우 낮은 경우) 구매자의 가치와 같은 S가 최적 제시액이 된다.
위 일계조건식 (3-2)의 좌변을 음함수 I(x)로 정의해 보자. 그러면 음함수 정리에 의해 S의 변화에 따른 최적 제시액의 변화를 알아볼 수 있다. 앞서의 가정들에 의해 다음의 식은 양수라는 것을 알 수 있다.
즉, 구매자의 가치가 높아질수록 구매자의 최적 제시액은 높아진다. 구매자가 거래를 통해 얻을 수 있는 가치 S가 충분히 크다면 구매자는 제시액을 높임으로써 판매자가 제시액을 받아들일 가능성을 높이려고 할 것이다. 따라서 S가 높아짐에 따라 구매자의 최적 제시액도 높아지는 것이다.
보조명제 1: 구매자는 판매자가 가지는 토지가치 V의 분포 F만 알고 있다고 가정하자. 이때 구매자가 판매자에게 단 한 번만 가격을 제시하고, 판매자는 제시된 가격에 대한 수락 여부를 결정할 기회를 단 한 번 가진다면, 구매자의 최적 제시액은 S가 커짐에 따라 증가한다.
증명) 음함수 정리와 식 (3-4)에 의해 증명된다. (증명 끝)
현실에서는 이같이 구매자나 판매자 중 어느 하나가 모든 협상력을 가지고 단 한 번 가격을 제시하는 경우는 드물다. 가격 제시와 협상이 양방향으로 반복적으로 이루어지는 가운데 최종적으로 거래가격이 정해진다. 비록 앞서 살펴본 경우들이 극단적이어서 비현실적일 수 있지만 한편으로는 가능한 양극단을 살펴봄으로써 현실에서의 실제거래를 예측하는 척도를 제공한다는 점에서 이들 경우를 살펴보는 것이 의미가 있다. 그리고 앞서 밝힌 대로 공공수용과정을 분석할 때 여기서 다룬 경우들이 일종의 기준 모형(benchmark model)의 역할을 할 수도 있을 것이다.
그러면 시장에서 거래되는 가격, 그리고 보상과 관련한 법 조항, 판례 등을 바탕으로 헌법에서 말하는 정당보상이 본 모형에서는 어떻게 적용될 수 있는지 살펴보겠다. 「토지보상법」 에서는 헌법에 명시된 정당보상과 관련해 보다 구체적인 원칙을 밝히고 있다. 이 중 본 모형과 밀접한 관련이 있는 대표적인 원칙으로 개발이익 배제, 그리고 객관적 가치에 대한 보상이라는 두 가지 원칙을 들 수 있다. 다시 말해서 토지소유자가 가지는 주관적인 가치는 제외하고서 수용보상액을 산정해야 하고 또한 개발에 따라 생기는 이익을 배제하면서 수용보상액을 산정해야 하는 것을 원칙으로 하고 있다.4)5)
본 연구에서는 이러한 법적 원칙, 법리적 해석, 그리고 법원의 판단 등에 대한 정당성이나 법률적 논의는 배제한다. 대신 법에서 추구하고자 하는 정당보상원칙에 따라 마련된 현재의 제도가 그 원칙을 달성하기 위해서 적합한지 그리고 개선되어야 할 점은 무엇인지 살펴보고자 한다.
그렇다면 법에서 정하고 있는 정당보상액을 본 모형에 어떻게 적용할 수 있는지 살펴보자. 우선 토지가치 V에 주관적 가치가 포함되어 있지 않는 경우는 피수용자에게 토지가치 V만큼 수용자가 보상액으로 지불하고 토지를 수용하는 것을 정당보상이라고 볼 수 있다. 그리고 공공사업을 통해서 추가적으로 생겨나는 사회적 이익 S − V를 개발이익으로 볼 수 있으며 정당보상액에는 이러한 개발이익이 배제되어야 한다.
그리고 토지가치 V에 객관적 가치와 주관적 가치가 모두 포함되어 있는 경우는 토지의 객관적 가치를 의미하는 기댓값 EV만큼 보상액으로 지불하는 것이 정당보상의 원칙에 부합한고 할 수 있다.6) 그리고 이 경우에는 S − EV를 개발이익이라고 할 수 있으며 보상액에 이러한 개발이익이 배제되어야 정당보상액이라고 할 수 있다. 따라서 이 경우는 EV가 정당보상액이다.
정의: 피수용자의 토지가치 중 객관적 가치 EV를 정당보상액이라 정의하고, 정당보상액이 지급되는 보상을 정당보상이라 정의한다.
이제부터 수용자가 피수용자의 토지를 수용하는 절차에 대한 모형을 바탕으로 각 참여자의 이해구조를 분석해 본다. 제2절과 제3절에서는 그 이해관계를 보다 명확히 이해하기 위해 수용자가 직접 보상액을 산정해서 피수용자에게 제시하는 모형을 다룬다. 그중 2절에서는 수용자가 피수용자의 토지가치에 대해서 정확히 알고 있는 경우(토지가치에 객관적 가치만 포함된 경우)를 다루고, 3절에서는 수용자가 피수용자의 토지가치에 대한 확률분포만을 아는 경우(토지가치에 객관적 가치와 주관적 가치가 모두 포함된 경우)를 다룬다. 이는 수용자의 정보 수준에 대한 양극단의 가정을 바탕으로 두 절에서 각각 분석함으로써 두 극단의 성질이 혼재되어 있는 현실에서의 인센티브 구조를 보다 잘 이해하기 위함이다.
우선 토지가치에 객관적 가치만이 포함되어 있어서 수용자가 토지가치에 대해서 정확히 알고 있는 경우의 모형을 살펴보자. 이 모형에서는 해당 토지를 이용한 공공사업계획이 확정된 후 수용자는 피수용자에게 보상액 x를 제시한다. 제시된 보상액에 대해서 피수용자가 받아들이면 보상이 진행되고 이에 따라 계획된 공공사업이 추진된다. 만약 제시된 보상액에 대해서 피수용자가 거부할 경우 수용위원회나 법원 같은 조정자의 조정절차를 거쳐서 최종적으로 보상액이 결정되고 수용이 이루어지게 된다. 본 모형에서는 조정단계에서 정해지는 보상액을 앞서 살펴본 정당보상액 V이라고 가정한다. 만약 보상액 조정절차를 거치는 경우는 협의에 의해 사업이 진행되는 경우에 비해 시간이 더 소요된다. 따라서 본 모형의 의사결정단계에서는 사업 지연에 따른 가치의 할인도 함께 고려해야 한다. 이러한 모형을 그림으로 표시하면 [Figure 1]과 같다.
[Figure 1]에나타나있듯이조정의 절차를 거치게 되면 수용자가 가지는 보수의 현재가치는 β ∈ (0 ,1)만큼 할인된다. 여기서 적용되는 할인율 β는 실질할인율의 개념에 더해서 사업 지연 및 분쟁과 관련하여 수용자가 지게 되는 정치적, 정책적 비용에 따른 가치 할인까지도 포함하는 개념이다. 공공사업이 시급성을 요하거나 정책적으로 의지가 강력하여 만약 사업이 지연되었을 시에는 사업을 시행하는 수용자의 정책적, 정치적, 사회적 부담이 큰 경우일수록 β가 작은 값을 가진다고 할 수 있다.7) 본 모형에서는 실질할인율 δ와 구분하기 위해 β를 공공할인율이라고 부르겠다. 할인율의 정의에 맞게 공공할인율 β는 실질할인율 δ보다 작은 값을 가진다고 할 수 있다.
여기서 또 하나 주목할 점은 피수용자 보수의 현재가치를 보면 조정을 거친 경우에도 할인이 되지 않은 것으로 표시되어 있다는 점이다. 금번 기에서 협상이 결렬되어 피수용자가 토지를 소유하고 있는 경우는 다음 기의 조정을 거치기 이전까지 그 기에 해당하는 토지의 가치를 가진다. 따라서 조정을 거친 경우 피수용자가 얻게 되는 최종 보수에는 조정을 거쳐 정해진 보상액의 현재가치와 더불어 협상이 결렬되어 토지를 소유함으로 인해 얻게 되는 가치도 함께 포함되어 있기 때문에 수용자의 보수와는 달리 피수용자의 보수가 할인되지 않는 것처럼 표시된다.8)
그러면 본 모형에서의 균형을 찾아보도록 하자. 본 모형에서 적용하는 균형의 개념은 부분게임 완전균형(subgame perfect equilibrium)이다. 이를 위해 우선 맨 아래 부분게임(subgame)에서 피수용자의 최적 전략을 살펴보자. 제시된 보상액을 거부하고 조정단계를 거칠 경우 피수용자가 가지는 보수의 현재가치는 V이다. 그러므로 제시된 보상액이 V보다 크거나 같으면 보상액을 받아들이고 그렇지 않으면 제시된 보상액을 거부하고 조정단계를 거치고자 한다. 이러한 피수용자의 전략하에서 수용자의 최적 전략은 당연히 피수용자의 토지에 대한 가치 V만큼 보상액으로 제시하는 것이다. 만약 V보다 낮은 값을 제시하면 조정단계를 거쳐야 하므로 수용자가 갖게 되는 보수는 V를 제시했을 때보다 β만큼 할인된다. 만약 V보다 높은 값을 보상액으로 제시하면 피수용자는 제시액을 받아들일 것이므로 V를 제시했을 때보다 더 많은 보상금을 피수용자에게 지급해야 하므로 최적의 전략이 될 수 없다. 따라서 피수용자의 토지에 대해 수용자가 토지가치인 V만큼 보상액으로 제시하고 이를 피수용자가 받아들이는 것이 이 게임의 부분게임 완전균형하에서의 결과라고 할 수 있다. 이러한 균형에서는 앞서 살펴본 법정신에 나타난 정당보상액이 실제 보상액으로 정해지고 이에 대해서 피수용자가 받아들인다는 점에서 최상의 결과(first best)라고 할 수 있겠다.
명제 1: 수용자가 피수용자의 토지가치를 알고 있는 경우, 부분게임 완전균형(subgame perfect equilibrium)에서 정당보상을 달성할 수 있다. 즉, 수용자는 피수용자에게 정당보상액을 지급하고 토지를 수용하는 결과(first best outcome)를 달성한다.
증명) 부록 참조
결론적으로 수용자가 토지가치에 대해서 정확히 아는 경우 부분게임 완전균형에서 달성되는 균형보상금은 정당보상금과 크기가 같다.
본 절에서는 토지가치에 객관적 가치와 주관적 가치가 모두 포함되어서 수용자가 토지가치에 대한 확률분포만을 아는 경우, 각 참여자의 균형전략은 어떻게 되는지 살펴보자. 본 절에서의 게임구조는 수용자의 정보에 대한 가정 이외에는 앞 절의 게임과 동일하다. 하지만 본 게임에서는 토지가치에 대한 피수용자의 주관적인 가치가 포함되어 있기 때문에 피수용자의 보수구조에는 앞서의 모형과는 차이가 있다. [Figure 2]를 보자.
수용자가 제시한 보상액에 대해서 피수용자가 수락하는 경우의 보수구조는 앞의 경우와 차이가 없다. 하지만 피수용자가 제시액을 거부한 경우의 보수구조는 차이가 있다. 우선 조정을 거친 경우 정해지는 조정보상액은 확률변수 D로 정해진다. 조정자의 입장에서는 해당 토지에 대한 객관적인 가치만을 반영하여 조정보상액을 산정하게 되는데 조정과정에서의 평가오차 등을 감안하여 확률변수로 정의하였다. 다만, 조정을 통해서 정해지는 조정보상액 D는 토지소유자가 가지는 토지가치 V와 기댓값은 같지만 분산이 작다고 가정한다.
가정 3: EV = ED, Var(V) > Var(D)
이는 현실에서 보상금에 관한 평가를 내릴 때 평가자 간의 주관적 견해와 판단의 차이에 따라 평가금액에 약간의 차이가 생길 수 있음을 반영하여 가정한 것이다.
조정을 거치는 경우 수용자는 공공사업에서 생겨나는 편익 S에 조정보상액을 뺀 만큼을 현재가치로 할인한 값을 가지게 된다. 피수용자의 경우 조정을 거치게되면 조정을 거치기 이전 기에는 객관적 가치와 주관적 가치를 모두 포함한 자신의 토지가치 중 현재 기에 누릴 수 있는 만큼 받고 조정 이후에는 조정보상액만큼 받게 된다. 피수용자가 만약 토지를 영원히 소유하고 토지로부터 매기 동일한 편익을 얻는다고 보면 조정 이전 기에 피수용자가 토지를 소유함으로써 얻는 편익은 (1 − δ)V라 할 수 있다. 여기서 δ는 앞서 정의한 바와 같이 피수용자에게 적용되는 실질할인율이다. 따라서 조정 이후 피수용자가 받는 기대조정보상액(EV)의 현재가치는 δ·EV이다. 이 둘을 합친 (1 − δ)V + δ·EV가 조정을 거쳤을 때 피수용자가 받는 보수이다.10)
이러한 게임구조에서 균형을 찾아보자. 이를 위해 우선 최하부 부분게임에서 피수용자의 의사결정을 살펴본다. 위의 보수구조에 의해 다음과 같은 피수용자 전략이 최하부 부분게임에서의 최적전략이다.
피수용자가 이러한 전략을 쓸 때 수용자의 의사결정 문제는 다음과 같다.
따라서 수용자의 최적 제시액은 다음 일계미분조건을 만족하는 값이 된다.11)
한편, 논의의 범위를 명확히 하기 위해 다음의 가정을 추가하고자 한다.
가정 4: 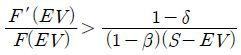
본 연구에서 공공사업을 통해 생겨나는 사회적 편익 혹은 개발이익 S가 공공사업 이전의 토지가치 V에 비해 상당히 크다고 가정하는 것에 큰 무리는 없다. 즉, 공공사업 진행을 결정하는 의사결정권자는 사회적 순편익을 감안하여 순편익이 충분한 규모로 예상될 때 공공사업을 진행하도록 결정한다는 의미이다.12) 또한 앞서 설명한 바와 같이 본 모형에서는 수용자와 피수용자가 가지는 할인율이 다르다. 그리고 수용자의 보수에 적용되는 공공할인율 β는 실질할인율 δ의 개념에 더해서 공공사업 추진 지연으로 인한 사회적, 정책적 비용에 따른 가치 할인의 개념도 함께 포함하고 있다. 그러므로 공공할인율 β는 실질할인율 δ에 비해 낮은 값을 가지게 된다. 본 모형에서는 이 둘의 값이 충분히 차이가 나는 상황을 가정하고 있다. 따라서 EV값이 S에 비해 상대적으로 상당히 낮은 값을 가진다는 점과 공공할인율이 실질할인율보다 상당히 낮은 값을 가진다는 점이 위 가정 3이 의미하는 바이다.
이러한 가정을 바탕으로 수용자의 최적 제시액 결정 문제를 살펴보면 다음의 명제가 성립한다.
명제 2: 수용자가 토지가치에 대한 확률 분포만을 알고 있는 경우, 균형에서 수용자가 피수용자에게 제시하는 보상액은 정당보상액보다 크다.
증명) 부록 참조
명제 2가 의미하는 바는 다음과 같다. 공공사업을 추진함에 있어서 기대할 수 있는 사회적 편익이 기존의 토지가치에 비해 상당히 클 것으로 예상된다면 수용자는 피수용자에게 정당보상액보다 어느 정도 많은 금액을 보상금으로 제시하고서라도 토지를 수용하는 것이 최적 전략이다.
그렇다면 이러한 균형이 파라미터 값이 변함에 따라 어떻게 변하는지 살펴보자. 다음의 따름명제가 이를 보여주고 있다.
따름명제 1: 수용자가 토지가치에 대한 확률분포만을 알고 있는 경우, 조정에 따른 가치의 할인이 많이 됨에 따라 혹은 해당 사업에서 기대하는 사회적 순편익이 증가함에 따라 균형에서 수용자가 피수용자에게 제시하는 보상액은 증가한다.
증명) 식 (3-6)의 일계미분조건식에 보조명제 1을 적용하면 된다. (증명 끝)
이러한 결과는 앞의 절에서 수용자가 토지가치에 대해 정확히 알고 있는 경우와 유사하다. 조정에 따른 가치 할인이 많이 되거나 해당 사업에 대한 사회적 기대 순편익이 높아질수록 조정절차로 인해 사업이 지연되는 데 따라 발생하는 손실이 더 커진다. 이에 따라 수용자는 조정을 거치지 않고 협의에 의해 보상이 이루어지는 것을 더 선호한다. 협의에 의한 보상을 더 선호할수록 수용자는 피수용자가 제시액을 거부할 확률을 낮추고자하므로 균형 제시액은 더 올라가게 된다.
지금까지 본 절에서는 부분게임 완전균형에서 피수용자가 (1 − δ)V + δ·EV를 기준으로 그보다 크거나 같으면 제시액을 받아들이고 그렇지 않으면 제시액을 거부하는 전략을 쓰는 경우를 살펴보았다.
앞서 살펴본 것처럼 수용자가 토지가치에 대하여 확률분포만을 알고 있는 경우 부분게임 완전균형에서는 수용자가 정당보상액 EV보다 큰 금액을 보상금으로 제시하고 피수용자는 이를 받아들인다. 다시 말해서 토지의 가치에 주관적 가치가 포함된 경우 수용자는 피수용자에게 정당보상액보다 많은 금액을 보상액으로 제시할 인센티브가 존재한다는 점이 본 절의 결론이다.
본 장에서는 수용자가 피수용자에게 직접 보상액을 제시하는 경우 달성되는 균형의 형태를 살펴보았다. 우선 수용자가 토지가치에 대한 정확한 정보를 가지고 있는 경우, 토지가치와 같은 가격을 피수용자에게 제시하고 이를 피수용자가 수용하는 것이 부분게임 완전균형의 결과임을 보였다. 한편, 수용자가 토지가치에 대하여 정확히 알지 못하고 가치에 대한 확률분포만을 아는 경우, 몇 가지 가정하에서 수용자는 토지가치의 기댓값보다 큰 값을 보상액으로 제시하고 피수용자는 이를 받아들이는 것이 부분게임 완전균형의 결과라는 것을 보였다. 그리고 이 경우 공공사업에서 기대할 수 있는 사회적 순편익이 클수록 혹은 사업 지연에 따른 사회적, 정책적 비용이 클수록 균형에서 수용자가 제시하는 금액은 더욱 커진다.
공공사업을 추진할 때 토지의 원소유자, 즉 피수용자가 강력히 반발하여 사업이 지연되면 수용자는 다양한 비용을 지불해야 한다. 사업 추진을 위해 사전적으로 조달해야 하는 자금에 대한 금융비용을 감당해야 하고 공공사업을 계획대로 추진하지 못함에 따른 정책적, 정치적 부담도 함께 감당해야 한다. 이러한 비용 때문에 수용자는 조정의 단계를 거치지 않고 협상의 단계에서 토지수용을 마무리하려는 인센티브가 생겨나고 이는 곧 정당보상액보다 큰 보상금이 지급되는 결과를 가져오게 된다. 그리고 그 비용이 더 커질수록 조정단계를 거치지 않으려는 인센티브가 더 커지고 이는 결국 과다보상이라는 결과에 이르도록 만들게 된다.
수용자가 가지는 이러한 인센티브와 더불어 피수용자 역시 당연하게 정당보상에 비해 많은 금액을 보상액으로 받으려는 인센티브가 존재한다. 결국 앞서 살펴본 모형하에서는 수용자와 피수용자 모두가 보상액을 정당보상액에 비해 높게 책정하고자 하는 인센티브가 존재할 수 있다. 보상액을 지급하는 쪽과 지급받는 쪽 모두가 정당보상액보다 높은 금액을 주고받을 인센티브가 존재하므로 결과적으로 과다보상이 일어날 개연성이 높음을 알 수 있다.
본 장에서는 앞서 제시한 기본모형에 더하여 피수용자가 토지수용에 대한 의사 표현을 할 수 있는 단계를 추가한다. 실제로 토지수용이 진행되는 과정에서 토지수용을 당하는 피수용자들은 토지수용에 대한 의사 표현을 하게 되고 이러한 의사 표현이 지나친 경우 격렬한 시위나 분쟁으로 이어지기도 한다. 이러한 점을 반영하여 본 장에서는 피수용자들이 토지수용에 대한 반발 수준(θ ∈ [0, 1] )을 정하고 이를 드러내는 단계를 모형에 추가하고자 한다. 이러한 단계를 통해 피수용자는 토지에 대한 자신의 주관적 가치를 일종의 신호(signalling)로서 수용자에게 보낼 수 있게 되고 이는 이후 보상금 산정단계에 영향을 미칠 수 있게 된다.[Figure 3]을 보자.
토지수용이 결정된 후 수용자가 피수용자에게 보상금 x를 제시하기 이전 단계에 피수용자는 해당 사업에 대하여 의견을 제시할 수 있다. 그림에서 보듯이 θ라는 값을 통해서 해당 사업에 대한 의견을 제시하게 되는데, 이때 θ값이 클수록 해당 사업과 토지수용에 대하여 반대의견을 강하게 표출하는 것으로 가정한다. 즉, θ값이 1에 가까울수록 토지수용에 대한 반대 의사가 강하여 피수용자가 강력한 물리적인 저항, 격렬한 시위 등을 벌이는 것으로 상정할 수 있다. 그리고 θ값이 0에 가까울수록 피수용자는 해당 토지의 수용에 대하여 별다른 저항을 하지 않는 것으로 상정한다. 이 같은 반발의 크기는 당연히 피수용자가 가지는 해당 토지의 가치에 영향을 받을 수 있다. 따라서 본 모형에서는 θ가 토지가치 V의 함수인 것으로 나타내고 있다. 실제로 이 함수가 어떤 형태를 가지는가는 본 게임의 균형전략에 의해서 결정될 것이다.
본 모형에서는 θ값이 수용자와 피수용자의 최종적인 보수에 영향을 미친다. 특히 θ값이 커질수록 실질할인율(δ)은 작아지는데, 이는 피수용자의 저항이 클수록 사업 진행속도가 느려지고 따라서 조정을 거쳐서 최종적으로 사업이 시행될 때까지 걸리는 시간이 오래 걸림에 따라 최종적인 보수에 적용되는 할인율이 더 낮아지기 때문이다. 또한 수용자의 공공할인율(β)은 θ값이 커짐에 따라 실질할인율(δ)이 작아지는 정도보다 더 많이 작아지게 된다. 이는 피수용자의 저항이 클수록 사회적 갈등이 커지고 이에 대한 수용자의 부담이 커지기 때문이다.
가정 5: β′(θ) < δ′(θ) < 0, 그리고 β″(θ) = δ″(θ) = 0 .
한편, 본 모형에서는 피수용자가 토지수용에 대해 저항을 할 때 그에 따르는 비용(C)을 부담하도록 가정하고 있다. 여기서 말하는 비용은 토지수용에 대한 반발을 하고 이에 대한 의사표현을 하기 위해 피수용자가 들여야 할 노력에서 생겨나는 비용을 의미한다. 물리적인 저항이나 반대 시위 등을 위해서는 피수용자가 자신의 노력과 시간을 들여야 한다는 점을 반영한 것이다. 본 모형에서는 이 비용함수 C(θ)는 θ가 증가함에 따라 볼록하게(convex) 증가한다고 가정한다.
가정 6: C′(θ) > 0, C″(θ) > 0.
그렇다면 이러한 모형에서 균형은 어떠한 모습일지 살펴보도록 하자.13)
우선 본 게임에서 분리균형은 존재하는지, 그리고 만약 존재한다면 어떠한 형태인지 살펴보도록 하자. 이를 위해 일단 본 게임의 분리균형이 존재한다고 가정한 후 이때 각각의 균형전략은 어떠한지 알아볼 필요가 있다.
피수용자가 자신의 토지가치 V에 따라 각각 다른 θ를 선택하는 분리균형이 존재한다고 하자. 그리고 이때의 피수용자의 균형전략을 θ*(V)라는 함수로 표현한다. 이 같은 균형하에서 수용자는 피수용자의 θ값을 보고 피수용자의 토지가치 V를 알 수 있다. 분리균형에서 수용자가 θ를 통해서 피수용자의 V를 아는 경우 수용자의 입장에서 최적 제시액 x*는 어떻게 결정되는지 살펴보자. 수용자는 제시액 x가 (1 − δ(θ*))V + δ(θ*)EV보다 크면 피수용자가 제시액을 받아들이고 그렇지 않으면 제시액을 거부한다는 것을 알고 있다. 만약 수용자가 제시액으로 (1 − δ(θ*))V + δ(θ*)EV를 제시하고 피수용자가 이를 수락하는 경우 수용자는 최종적으로 S − [(1 − δ(θ*))V + δ(θ*)EV]만큼 받게 된다. 그렇지 않고 제시액을 거부하는 경우 수용자는 β(θ*)(S − EV)만큼 받게 된다. 그리고 두 보수를 비교하면 앞서의 가정들에 의해 수용자는 피수용자가 제시액을 거부하는 것보다 (1 − δ(θ*))V + δ(θ*)EV의 제시액을 받아들이는 것을 더 선호한다. 따라서 다음의 보조명제와 같이 정리할 수 있다.
보조명제 2: 피수용자의 반발 정도를 나타낼 수 있는 모형에서 만약 피수용자가 V에 따라 다른 값의 θ*(V)를 드러내는 분리균형이 존재한다면 수용자는 (1 − δ(θ*))V + δ(θ*)EV를 제시액으로 제시하고 피수용자는 이를 수락한다.
증명) 본문에 정리됨. (증명 끝)
실제로 이 같은 분리균형이 존재하는지를 살펴보기 위해서는 위 보조명제와 같은 균형하에서 피수용자가 θ*(V)를 통해 자신의 토지가치를 솔직하게 드러낼 것인가를 살펴보아야 한다. 그러면 분리균형하에서 피수용자의 반발 정도 결정과정을 살펴보자. 피수용자의 결정에는 다음과 같이 수용자가 위의 분리균형에서 제시하는 보상액 (1 − δ(θ*))V + δ(θ*)EV가 영향을 미친다.
우선 V > EV인 경우를 살펴보자. 위 최대화 문제의 일계미분조건을 통해 각 V에 따른 최적의 θ가 결정된다.14) 또한 음함수 정리를 사용하여 일계미분조건으로부터 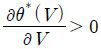 인 것을 알 수 있다. 즉, 위에서 상정한 분리균형에서는 V > EV인 경우, V값이 증가함에 따라 최적의 반발 정도가 증가하게 된다. 한편, V ≤ EV인 경우는 위 최대화 문제로부터 최적의 반발 정도는 항상 0임을 알 수 있다. 즉, 위에서 상정한 분리균형하에서는 V ≤ EV인 경우, V의 값에 상관없이 최적의 반발 정도로 0을 선택한다. 이를 통해 θ*(V)가 결정된다.
인 것을 알 수 있다. 즉, 위에서 상정한 분리균형에서는 V > EV인 경우, V값이 증가함에 따라 최적의 반발 정도가 증가하게 된다. 한편, V ≤ EV인 경우는 위 최대화 문제로부터 최적의 반발 정도는 항상 0임을 알 수 있다. 즉, 위에서 상정한 분리균형하에서는 V ≤ EV인 경우, V의 값에 상관없이 최적의 반발 정도로 0을 선택한다. 이를 통해 θ*(V)가 결정된다.
하지만 이 같은 θ*(V)가 분리균형하에서 성립되기 위해서는 각각의 V값을 가진 피수용자가 다른 V값을 가진 피수용자인 것처럼 행동할 유인이 없는지 살펴봐야 한다. 각각의 피수용자가 어떤 값을 가진 것으로 행동하는 것이 각자에게 최적인지를 알아보기 위한 최적화 문제는 다음과 같다.
위 식에서 V′는 실제로는 V라는 토지가치를 가진 피수용자가 반발 정도를 통해 자신의 타입인 것처럼 드러내기로 결정한 토지가치값을 의미한다. 위 식을 보면 피수용자의 실제 토지가치 V와 상관없다는 것을 알 수 있다. 그리고 이는 곧 피수용자의 실제 토지가치와는 상관없이 최적인 V′가 존재한다는 것을 알 수 있다.15) 위 목적함수를 일계미분한 식은 the envelop theorem에 의해 다음 부등식의 좌변과 같이 표현되며, 이는 가정에 의해 항상 0보다 크다.
이는 결국 위의 목적함수가 V′의 증가함수임을 의미하며, V′ = V 일 때 최댓값을 가진다. 즉, 피수용자는 위의 분리균형하에서 자신의 토지가치에 상관없이 최대의 토지가치를 가진 것처럼 반발 정도를 나타내는 것이 최적이므로 앞서 살펴본 분리균형이 존재할 수 없음을 알 수 있다.
명제 3: 토지수용에 대하여 피수용자의 반발 정도(θ)를 정할 수 있는 모형에서 피수용자의 토지가치에 따라 다른 반발 정도를 제시하는 분리균형은 존재하지 않는다.
증명) 본문에 정리됨. (증명 끝)
그리고 위의 논의를 통해 일부만 자신의 토지가치를 드러내는 부분분리균형도 존재할 수 없음을 알 수 있다. 만약 자신의 토지가치를 드러내는 일부의 피수용자가 있는 경우, 수용자는 (1 − δ(θ*))V + δ(θ*)EV를 보상액으로 제시할 것이다. 이때에도 위의 명제 3에서와 마찬가지로 피수용자는 자신의 토지가치를 드러내는 것보다는 토지가치를 드러내는 유형 중 토지가치가 가장 높은 유형인 것으로 속이는 것이 더 낫다. 결국 부분분리균형도 존재할 수 없다. 이는 본 모형의 균형을 찾기 위해서는 분리균형이 아니라 공용 균형에 대해서 살펴봐야 한다는 것을 의미한다.
그러면 이제부터는 피수용자가 항상 같은 수준의 반발 정도를 정하는 공용균형에 대해서 살펴보자. 이를 위해 우선 모든 타입의 피수용자가 반발 수준  를 선택하는 공용균형이 성립되기 위해서 어떠한 조건들이 만족되어야 하는지 살펴볼 필요가 있다.
를 선택하는 공용균형이 성립되기 위해서 어떠한 조건들이 만족되어야 하는지 살펴볼 필요가 있다.
주어진  하에서 수용자는 앞의 장에서 최적 제시액 x*를 정할 때와 유사한 다음의 최적화 문제를 풀어서 최적의 제시액 x*(
하에서 수용자는 앞의 장에서 최적 제시액 x*를 정할 때와 유사한 다음의 최적화 문제를 풀어서 최적의 제시액 x*( )를 결정한다.
)를 결정한다.
그러면 피수용자는 제시액 x*( )가 (1 − δ(
)가 (1 − δ( ))V + δ(
))V + δ( )EV보다 크거나 같으면 이를 수락하고 그렇지 않으면 이를 거부한다. 이 같은 결과가 균형이 되기 위해서는 우선 수용자의 최적 제시액 x*를 거부하는 피수용자에게
)EV보다 크거나 같으면 이를 수락하고 그렇지 않으면 이를 거부한다. 이 같은 결과가 균형이 되기 위해서는 우선 수용자의 최적 제시액 x*를 거부하는 피수용자에게  가 자신의 보수 (1 − δ(θ))V+ δ(θ)EV − C(θ)를 극대화하는 값이어야 한다. 만약 그렇지 않다면 피수용자는
가 자신의 보수 (1 − δ(θ))V+ δ(θ)EV − C(θ)를 극대화하는 값이어야 한다. 만약 그렇지 않다면 피수용자는  가 아닌 다른 반발 수준을 나타낸 후 수용자의 제시액을 거부하면 더 큰 이익을 얻을 수 있기 때문이다. 그리고 최적 제시액 x*를 수락하는 피수용자는 균형하에서의 보수 x* − C(
가 아닌 다른 반발 수준을 나타낸 후 수용자의 제시액을 거부하면 더 큰 이익을 얻을 수 있기 때문이다. 그리고 최적 제시액 x*를 수락하는 피수용자는 균형하에서의 보수 x* − C( )가 제시액을 거부했을 때 얻을 수 있는 최댓값인 maxθ(1 − δ(θ))V + δ(θ)EV − C(θ)보다 커야 한다. 만약 그렇지 않을 경우 피수용자는 균형 반발 수준이 아니라 제시액 거부 시 자신이 얻을 수 있는 보수를 최대로 만드는 반발 수준을
택하고 또한 수용자의 제시액을 거부함으로써 더 큰 이익을 얻을 수 있게 된다. 따라서 반발 수준이
)가 제시액을 거부했을 때 얻을 수 있는 최댓값인 maxθ(1 − δ(θ))V + δ(θ)EV − C(θ)보다 커야 한다. 만약 그렇지 않을 경우 피수용자는 균형 반발 수준이 아니라 제시액 거부 시 자신이 얻을 수 있는 보수를 최대로 만드는 반발 수준을
택하고 또한 수용자의 제시액을 거부함으로써 더 큰 이익을 얻을 수 있게 된다. 따라서 반발 수준이  인 공용균형이 성립되기 위해서는 다음의 조건이 만족되어야 한다.
인 공용균형이 성립되기 위해서는 다음의 조건이 만족되어야 한다.
조건 1:
∀V,  = argmax θM(θ),
= argmax θM(θ),
where M(θ) = max {x*(θ) − C(θ), } {(1 − δ(θ*))V + δ(θ)EV − C(θ) }
다음에서는 반발 수준이  인 공용균형이 존재하는 것과 위의 조건 1을 만족하는
인 공용균형이 존재하는 것과 위의 조건 1을 만족하는  가 존재하는 것이 동치임을 명제를 통해 보여주고 있다.
가 존재하는 것이 동치임을 명제를 통해 보여주고 있다.
명제 4: 조건 1을 만족시키는  가 존재하는 것과 반발 수준이
가 존재하는 것과 반발 수준이  인 공용균형이 존재하는 것은 동치이다.
인 공용균형이 존재하는 것은 동치이다.
증명) 부록 참조
이를 바탕으로  값의 범위에 따라 균형이 어떠한 형태를 띨 것인지 보다 자세히 알아보겠다. 이를 위해 우선 피수용자가 제시액을 거부했을 때 얻게 되는 보수 (1 −
δ(θ))V + δ(θ)EV − C(θ)에 대해 살펴볼 필요가 있다. 이에 대한 일계미분조건을 다시 써보면 다음과 같다.
값의 범위에 따라 균형이 어떠한 형태를 띨 것인지 보다 자세히 알아보겠다. 이를 위해 우선 피수용자가 제시액을 거부했을 때 얻게 되는 보수 (1 −
δ(θ))V + δ(θ)EV − C(θ)에 대해 살펴볼 필요가 있다. 이에 대한 일계미분조건을 다시 써보면 다음과 같다.
위 식 (4-3)의 우변은 C(θ) 함수와 δ(θ) 함수에 대한 가정에 의해 θ에 대해서 증가한다.16) 그리고 우변은 항상 양의 값을 갖는 데 반해 좌변은 V의 값에 따라서 달라진다. 이는 결국 V가 EV보다 작은 피수용자의 경우  > 0인 범위의 반발 정도를 나타내는 공용균형에서는 항상 제시액 x*(
> 0인 범위의 반발 정도를 나타내는 공용균형에서는 항상 제시액 x*( )를 수락하는 결정을 내린다는 것을 의미한다.
)를 수락하는 결정을 내린다는 것을 의미한다.
또한 각 V값에 따라 위 일계조건을 만족하는 θ값이 다르다는 점을 통해서 알 수 있는 점은,  ∈(0, 1)의 범위에 있는
∈(0, 1)의 범위에 있는  를 반발 정도로 나타내는 공용균형에서는 V를 가진 피수용자가 제시액을 거부했을 때 얻을 수 있는 보수만큼을 보장하도록 보상금 x*가 제시되어 아무도 제시액을 거부하지 않아야 한다는 점이다.17) 만약 이보다 낮은 액수가 보상금으로 제시되어 V를 가진 피수용자를 비롯하여 제시액을 거부하는 피수용자의 타입이 복수인 경우는 각각의 피수용자에게 최적인 반발 수준은 각각 다르게 결정된다. 따라서
반발 수준
를 반발 정도로 나타내는 공용균형에서는 V를 가진 피수용자가 제시액을 거부했을 때 얻을 수 있는 보수만큼을 보장하도록 보상금 x*가 제시되어 아무도 제시액을 거부하지 않아야 한다는 점이다.17) 만약 이보다 낮은 액수가 보상금으로 제시되어 V를 가진 피수용자를 비롯하여 제시액을 거부하는 피수용자의 타입이 복수인 경우는 각각의 피수용자에게 최적인 반발 수준은 각각 다르게 결정된다. 따라서
반발 수준  ∈(0,1)을 나타내는 공용균형이 존재할 수 없다. 즉, 모서리 값(0 혹은 1)이 아닌 내부값을 가진
∈(0,1)을 나타내는 공용균형이 존재할 수 없다. 즉, 모서리 값(0 혹은 1)이 아닌 내부값을 가진  를 가지는 공용균형에서는 V를 가진 피수용자가 제시액을 거부했을 때 얻는 보수만큼을 보장하는 보상금이 제시되어 아무도 제시액을 거부하지 않게 된다.
를 가지는 공용균형에서는 V를 가진 피수용자가 제시액을 거부했을 때 얻는 보수만큼을 보장하는 보상금이 제시되어 아무도 제시액을 거부하지 않게 된다.
보조명제 3: 피수용자의 반발 정도가 내부값( ∈(0,1))을 가지는 공용균형에서는
∈(0,1))을 가지는 공용균형에서는 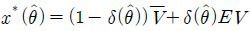 가 제시되고 이에 대해서 어떠한 피수용자도 이를 거부하지 않는다.
가 제시되고 이에 대해서 어떠한 피수용자도 이를 거부하지 않는다.
증명) 본문에 설명됨. (증명 끝)
이 같은 경우에 대한 직관적인 설명은 다음과 같다. 수용자의 공공할인율 β(θ)가 피수용자의 반발 정도(θ)에 매우 민감하게 반응하여 조금의 반발에도 공공할인율이 상당히 많이 떨어지는 경우 수용자의 최적 제시액 x*(θ)는 상당히 높게 형성되어 피수용자 모두가 수락을 할 보상금이 제시되는 균형이 성립될 수 있는 것이다.
반면,  가 0 혹은 1로서 공용균형을 이루는 경우는 상당히 다른 형태를 띠게 된다. 반발 정도가 내부값을 가지는 경우와는 달리 모서리값(0 또는 1)을 균형
반발 정도로 가지는 공용균형에서는 모서리 해의 특성상 제시액을 거부하는 피수용자의 타입이 복수로 존재할 수 있다. 이는 특정 V값들에 대해서 식 (4-3)을 만족하는 θ가 [0,1]의 범위 밖에 있어서 θ가 가능한 범위 내에서는 일계미분식이 부등식으로 만족하는 경우를 의미한다. 다음의 부등식을 보자.
가 0 혹은 1로서 공용균형을 이루는 경우는 상당히 다른 형태를 띠게 된다. 반발 정도가 내부값을 가지는 경우와는 달리 모서리값(0 또는 1)을 균형
반발 정도로 가지는 공용균형에서는 모서리 해의 특성상 제시액을 거부하는 피수용자의 타입이 복수로 존재할 수 있다. 이는 특정 V값들에 대해서 식 (4-3)을 만족하는 θ가 [0,1]의 범위 밖에 있어서 θ가 가능한 범위 내에서는 일계미분식이 부등식으로 만족하는 경우를 의미한다. 다음의 부등식을 보자.
위의 부등식은 반발 정도가 1인 공용균형에서 제시액을 거부하는 피수용자의 타입이 복수로 존재하기 위한 필요조건이다. 즉, 반발 정도가 1인 공용균형에서 제시액을 거부하는 피수용자 타입이 복수로 존재하기 위해서는 특정 V값들에 대해서 일계미분식을 등식으로 만족하는 θ가 1보다 커야 한다. 반대로 반발 정도가 0인 공용균형에서 제시액을 거부하는 피수용자 타입이 복수로 존재하기 위해서는 다음의 부등식을 만족해야 한다.
결론적으로 위의 조건 1을 만족하는 θ가 내부 해를 가지는 경우는 공용균형에서 제시액을 거부하는 피수용자의 타입 수는 최대로 1개(V)가 가능하지만 모서리 해를 가지는 경우는 그 타입 수가 여러 개인 것이 가능하다.
이상의 균형에 대한 논의에서 특이할만한 점은 각각의 공용균형에서 정해지는 균형 반발 수준은 토지가치가 V인 피수용자가 제시액을 거부했을 시 얻게되는 보수를 최대화시키는 θ값이라는 점이다. 이에 대해 공용균형에서 토지가치가 V인 피수용자가 제시액을 거부하는지 제시액을 수락하는지 여부에 따라 나눠서 살펴봐야 한다.
토지가치가 V인 피수용자가 제시액을 거부하는 공용균형의 경우를 보면, 해당 피수용자는 항상 자신의 보수를 극대화하는 반발 수준을 택할 것이므로 이 반발 수준과 공용균형에서의 균형 반발 수준은 같아야 한다. 그리고 토지가치가 V인 피수용자가 제시액을 수락하는 공용균형을 보면 수용자는 토지가치가 V인 피수용자가 제시액을 수락토록 하기 위해서 토지가치가 V인 피수용자가 제시액을 거부했을 시 얻게 되는 보수만큼을 보장하는 금액을 제시한다. 이는 피수용자가 택한 θ값에 따라 달라지게 되므로 토지가치가 V인 피수용자는 제시액을 거부했을 시 얻게 되는 보수를 최대로 만드는 반발 수준을 택할 것이다. 따라서 이 경우에도 토지가치가 V인 피수용자가 제시액을 거부했을 시 얻게 되는 보수를 최대로 만드는 반발 수준이 공용균형에서의 반발 수준과 같게 된다. 이를 정리하면 다음과 같은 보조명제가 된다.
보조명제 4: 공용균형하에서 정해지는 반발 수준은 토지가치가 가장 높은 피수용자가 수용자의 제시액을 거부했을 때 얻는 보수를 최대로 만드는 반발 수준과 같다.
증명) 본문에 설명됨. (증명 끝)
지금까지 피수용자가 반발 정도를 사전적으로 정할 수 있는 모형에서의 균형에 대해서 살펴보았다. 본 균형을 통해서 보았을 때 주어진 외생변수들에 따라 피수용자는 자신의 토지가치와는 상관없이 일정한 수준(토지가치가 V인 피수용자가 제시액 거부 시 얻게 되는 보수를 최대로 만드는 반발 수준)의 반발을 하는 것이 균형전략이라는 점을 알 수 있다.
실제 토지수용과정에서는 다양한 이유로 인해 수용에 대한 반발과 갈등이 생겨날 수 있다. 본 모형에서는 그중 피수용자의 전략적 선택에 의해서도 이 같은 반발과 갈등이 생길 수 있다는 점을 중점적으로 보여주고 있다. 이를 바탕으로 다음 장에서는 피수용자의 전략적 반발과 수용자의 과다보상 유인 문제를 개선하기 위한 방안을 논의하고자 한다.
앞의 제Ⅲ장과 제Ⅳ장에서는 법에서 의도하는 정당보상에 비해 많은 보상금이 균형에서 정해질 유인이 있음을 살펴보았다. 이와 더불어 제Ⅳ장에서는 피수용자가 자신의 보상금을 높이기 위해 전략적으로 공공수용에 대해 사회적 갈등을 일으킬 가능성이 있음을 보였다. 본 장에서는 이 같은 과다보상 유인과 전략적 갈등유발 유인을 줄일 수 있는 개선방향에 대해서 살펴보고자 한다.
계약이론과 기업 지배구조이론 분야에서는 자신의 권한을 상대방에게 혹은 외부인에게 위임하여 이해관계의 상충을 개선하고 보다 나은 결과를 달성하는 상황에 대한 연구가 진행되어 왔고, 이는 현실에서도 종종 목격되고 있다.18) 본 장에서는 보상액 산정 및 제시에 관한 권한을 객관적 평가자에게 위임함으로써 앞서의 모형에 비해 법에서 의도하는 정당 보상액에 근접한 균형을 달성할 수 있음을 보이고자 한다.
본 절에서는 앞서 다룬 게임모형들에서 보상액 산정 및 제시를 수용자가 아닌 제3자가 대신했을 경우 그 균형이 어떻게 달라지는지 살펴보고자 한다. 여기서 말하는 제3자란 토지에 대한 보상액 평가와 관련하여 어떠한 이해관계도 없고 평가를 위한 어떠한 노력도 들일 필요가 없는 평가자를 의미한다. 우선 객관적 토지가치만이 존재하여 수용자가 그 가치를 정확히 알고 있을 때의 게임모형을 중심으로 보상액 평가 및 제시 권한이 제3의 평가자에게 위임되었을 때의 균형을 살펴보자. 게임모형을 그림으로 표현하면 [Figure 4]와 같다.
앞서 언급한 대로 본 절에서의 게임과 [Figure 1]에서 나타난 게임의 차이점은 수용자 대신 객관적인 평가자가 피수용자에게 보상액을 제시한다는 점이다. 이 때 평가자는 게임의 결과에 상관없이 고정된 수수료 K를 보수로 받게 된다.
그렇다면 본 모형에서는 어떠한 균형에 도달될지 살펴보자. 보상액이 제시된 이후 하부 게임에서 피수용자의 최적 전략은 앞의 제Ⅲ장 제2절에서의 최적 전략과 같다. 즉, 제시액이 V보다 크거나 같으면 이를 수락하고 그렇지 않으면 거부하는 전략이 피수용자에게 최적이다. 이러한 전략하에서 평가자는 어떠한 제시액을 제시하더라도 자신의 보수에는 변화가 없다. 평가자는 자신의 보수에 차이가 없는 한 토지가치인 V를 제시한다고 보아도 무방하다.19)
따라서 본 모형에서의 부분게임 완전 균형에서는 정당보상액이 제시되고 이를 피수용자가 수락하게 된다. 그리고 평가자가 토지의 객관적 가치인 V를 항상 제시하는 경우는 이 부분게임 완전균형이 유일한 균형이 된다. 이 점이 앞서 제Ⅲ장 제2절에서 살펴본 모형과 가장 큰 차이이다. 수용자가 직접 보상액을 제시할 때와는 달리 평가자가 보상액을 제시하는 경우는 피수용자가 어떠한 전략을 쓰더라도 평가자의 인센티브 구조가 달라지지 않는다. 결국 피수용자가 원하는 균형을 유도하기 위한 전략적 위협이 유효하지 않게 되어 균형에서는 정당보상액이 제시되고 피수용자는 이를 받아들이게 된다.
명제 5. 토지에 대한 객관적 가치만 존재하고 수용에 따른 보상액을 수용자 대신 권한을 위임받은 평가자가 제시하는 경우, 정당보상액이 제시되고 이를 피수용자가 수용하는 균형만이 유일하게 달성 가능하다.
증명) 최하부 게임에서의 피수용자 전략과 상관없이 평가자는 정당보상액을 제시하는 것이 최적 전략이다. 따라서 평가자는 항상 정당보상액을 제시하게 되고 피수용자는 이를 수용하게 된다. (증명 끝)
위의 명제에서 볼 수 있듯이 수용자는 보상액을 제시하는 권한을 제3자인 평가자에게 전적으로 위임함으로써 조정과정없이 정당보상액을 지급하는 균형을 달성할 수 있다. 여기서 핵심적인 내용은 제3자로의 전적인 권한위임이다. 만약 권한을 위임하였어도 여전히 수용자가 위임받은 자의 결정에 영향을 미칠 수 있다면 권한을 위임하기 이전과 같은 결과를 가져오게 된다. 따라서 권한위임을 통하여 보다 바람직한 균형에 도달하고자 할 때에는 수용자의 영향력 밖에서 평가자가 결정을 내릴 수 있는 법적, 제도적 장치가 필요하다. 이를 통해 게임의 참가자 모두가 권한위임과 평가자의 중립성에 신뢰를 가질 수 있을 때 명제 5와 같은 균형을 달성할 수 있는 것이다.
다음으로 토지가치에 객관적 가치와 주관적 가치가 모두 포함되어 있는 경우를 살펴보자. 여기서 다루고자 하는 게임모형을 표현하면 [Figure 5]와 같다.
제Ⅲ장 제3절에서의 모형과 가장 큰 차이점은 수용자 대신 평가자가 피수용자에게 보상액을 제시한다는 점이다. 앞서의 권한위임모형에서와 마찬가지로 평가자는 게임의 결과와는 상관없이 고정된 수수료를 받게 되고 따라서 게임 결과와 관련한 아무런 인센티브도 가지지 않게 된다. 이때 평가자는 정당보상액인 EV를 제시한다고 가정하여도 전혀 무리가 없다. 평가자가 EV를 제시하면 피수용자는 이를 수락하거나 거부하게 된다. 피수용자의 입장에서는 앞의 제Ⅲ장 3절의 경우와 마찬가지로 제시액 x와 조정시의 보수 (1 − δ)V + δEV를 비교하여 제시액을 수락할지 거부할지 결정하게 된다. 피수용자는 자신의 토지가치 V가 EV보다 큰 경우는 조정 시의 보수 (1 − δ)V + δEV가 제시액 EV보다 크므로 제시액을 거부하게 된다. 또한 피수용자의 토지가치 V가 EV보다 작은 경우는 제시액 EV가 조정 시의 보수 (1 − δ)V + δEV보다 크므로 제시액을 받아들이게 된다. 다시 말해서 만약 피수용자의 토지가치 V가 EV보다 작은 경우는 제시액을 수락하게 될 것이고, 토지가치 V가 EV보다 큰 경우는 거부를 하여 조정의 단계를 거쳐서 EV를 보상액으로 받게 될 것이다. 결국 어떠한 결과에 대해서도 피수용자에게 지급되는 보상액은 정당보상액인 EV가 되므로 본 게임모형에서는 항상 정당보상이 달성된다고 할 수 있다.
명제 6: 피수용자의 토지가치에 대한 객관적 가치와 주관적 가치가 모두 존재하고 수용자에게서 권한을 위임받은 평가자가 보상액을 제시하는 경우, 균형에서 정당보상이 달성된다.
증명) 본문에 설명됨. (증명 끝)
앞서 살펴본 명제 2에서의 과다보상 유인이 위 명제 6에서는 사라졌음을 알 수 있다. 이는 곧 감정평가업무가 정당보상과 상당히 밀접한 관계에 있음을 보여주고 있다. 즉, 현재의 감정평가제도가 도입된 가장 큰 이유 중 하나가 권한위임을 통해 정당보상을 달성하기 위함이라고 볼 수 있다. 감정평가업무의 전문성을 차치하더라도 정당보상의 달성을 위해 감정평가업무는 매우 중요한 의미를 가진다.
또한 명제 6에서 주요 가정 중의 하나는 수용자나 피수용자가 감정평가업무에 영향을 미칠 수 없다는 점이다. 결국 정당보상에 보다 근접하기 위해서는 감정 평가업무가 수용자나 피수용자의 이해관계에서 최대한 독립적이도록 만들어야 한다는 점을 명제 6은 내포하고 있다. 하지만 현실에서는 감정평가업무가 완벽히 독립적으로 이루어지고 있다고는 볼 수 없다. 따라서 감정평가업무의 독립성을 강화시키기 위한 정책적인 노력이 필요할 것이다. 이 부분에 대해서는 다음 제2절과 제3절에서 본격적으로 논의하도록 하겠다.
이어서 제Ⅳ장에서와 같이 피수용자가 반발 수준(θ)을 결정하는 경우의 권한위임모형을 살펴보자. 게임의 구조는 [Figure 6]과 같다. 여기서도 앞서의 경우와 마찬가지로 평가자는 항상 평가액으로 EV를 제시하는 것으로 상정한다. 그 경우 우선 V가 EV보다 작거나 같은 피수용자는 평가액 EV를 항상 수락한다. 또한 반발에 따른 비용을 최소화하기 위해서 사전적인 반발 수준(θ)은 0으로 하는 것이 최선이다. 반면, V가 EV보다 큰 피수용자는 평가액 EV를 거절하여 조정의 단계를 거친다. 이때 피수용자의 최적 반발 수준은 제시액을 거절했을 때의 자신의 보수 (1 − δ(θ))V + δ(θ)EV − C(θ)를 최대화하는 θ를 정한다.
여기서 흥미로운 점은 피수용자의 반발 수준이다. 앞서의 제Ⅳ장에서의 모형과는 달리 V ≤ EV인 경우에는 토지가치에 상관없이 똑같은 반발 수준(θ = 0)을 선택하고 V > EV인 경우에는 각 가치별로 보수를 최대화하기 위한 θ값을 선택한다. 앞의 식 (4-3)은 V > EV인 경우 피수용자의 보수 최대화를 위한 일계 조건을 보여준다. 이를 바탕으로 [Figure 7]에서는 피수용자의 최적 반발 수준을 보여주고 있다.
식 (4-3)의 우변이 θ의 증가함수이므로 V ≥ EV인 범위에서는 V가 증가함에 따라 최적의 반발 수준 θ도 증가하다가 상한값인 1에서 증가를 멈추게 된다. 만약 V가  보다 작은 경우는 V ≥ EV 범위에서는 각 V에 따라 다른 값의 θ를 정하게 되고, 만약 V가
보다 작은 경우는 V ≥ EV 범위에서는 각 V에 따라 다른 값의 θ를 정하게 되고, 만약 V가 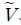 보다 큰 경우는 EV ≤ V ≤
보다 큰 경우는 EV ≤ V ≤ 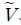 에서는 각 V에 따라 다른 값의 θ를 정하고,
에서는 각 V에 따라 다른 값의 θ를 정하고, 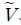 ≤ V ≤ V에서는 모두 반발 수준으로 1을 택한다.
≤ V ≤ V에서는 모두 반발 수준으로 1을 택한다.
이를 통해 알 수 있는 것은 각 타입의 피수용자는 V의 토지가치를 가진 피수용자의 반발 수준보다 항상 작거나 같은 수준의 반발 정도를 정한다는 점이다. 그리고 이를 앞서의 보조명제 5의 내용과 종합해 보면 제Ⅳ장에서의 공용균형보다 본 모형에서의 균형에서 사전적으로 기대할 수 있는 반발 수준이 더 낮다는 것을 알 수 있다. 제Ⅳ장에서 다룬 공용균형에서는 균형 반발 수준이 항상 V의 토지가치를 가진 피수용자가 제시액을 거부했을 때 얻게 되는 보수를 극대화시키는 값이었다. 하지만 본 모형에서는 우선 V ≤ EV의 토지가치를 가진 피수용자는 반발 수준을 0으로 정하고 그 외의 피수용자의 반발 수준도 최댓값이 V의 토지가치를 가진 피수용자가 제시액을 거부했을 때 얻게 되는 보수를 극대화시키는 값이다. 따라서 제Ⅳ장에서의 공용 균형일 때에 비해 본 권한위임모형에서의 균형일 때 사전적으로 더 낮은 반발 수준을 기대할 수 있다.
명제 7: 토지가치에 대한 피수용자의 객관적 가치와 주관적 가치가 모두 존재하고, 피수용자의 반발 정도(θ)를 사전적으로 정할 수 있으며, 수용자에게서 권한을 위임받은 평가자가 보상액을 제시하는 경우, 균형에서 정당보상이 달성된다. 그리고 사전적인 기대 반발 수준은 권한위임 시의 기대 반발 수준이 그렇지 않을 때의 기대 반발 수준보다 더 낮다.
증명) 본문에 설명됨. (증명 끝)
명제 5~7을 통해서 권한위임을 통해 과다보상의 유인을 차단하고 정당보상에 근접할 수 있음을 보였다. 또한 권한위임시에 수용에 따른 피수용자의 전략적 반발 수준도 낮출 수 있음도 보였다. 따라서 정당보상을 달성하기 위한 효과적인 제도를 연구하기 위해서는 현실에서의 권한위임제도가 이상적인 형태의 권한위임제도와 어떤 차이가 있는지 살펴보고, 현실에서의 권한위임제도를 이상적인 형태에 보다 근접하도록 만들기 위한 개선방안을 살펴볼 필요가 있다.20)
현실에서는 보상액 산정을 수용자가 직접 하지 않고 전문자격사인 감정평가사가 그 업무를 하도록 되어 있다. 다음 절에서는 이러한 감정평가사제도가 앞서 살펴본 정당보상 달성수단으로서의 권한위임의 기능을 제대로 수행하고 있는지를 살펴보고자 한다.
정당보상액이 제시되는 균형에 가까이 가기 위해 토지보상법에서는 보상액 평가 및 산정 업무를 수용자가 아닌 감정평가사가 하도록 정하고 있다. 이는 감정평가업무가 전문성을 요구하기 때문에 국가에서 공인하는 전문자격사로 하여금 그 업무를 처리하도록 하는 취지가 있고 이와 동시에 상대적으로 이해관계에서 벗어나 있는 제3자로 하여금 평가를 내리도록 하여 보상 제시액과 정당보상액 간의 차이를 줄이고자 하는 취지도 있다고 볼 수 있다.
본 연구에서는 감정평가사의 역할 중 후자에 비중을 두어 살펴보고 있다. 하지만 보상액 평가업무를 감정평가사에게 위임하는 것만으로 정당보상액이 제시되는 균형에 도달한다고 보기에는 현실적으로 어려움이 있다. 여기서는 앞서 살펴 본 모형이 현실과는 어떤 점에서 차이가 있는지 살펴보도록 하겠다.
본 절에서는 감정평가업무에 있어서 평가사 간 주관적 판단과 소신의 차이에 따라 평가액이 달라지는 점을 감안하여 몇 가지 가정을 추가한 모형을 다루고자 한다. 지금까지 토지의 가치 중 객관적인 가치에 대해서는 누구나 알고 있다고 가정하였다. 그러므로 앞 절에서는 토지가치 평가에 대한 권한을 제3의 평가자에게 위임하였을 때 그 평가자는 토지의 객관적 가치 V를 보상액으로 제시하는 균형을 달성할 수 있었다. 하지만 실제로 똑같은 토지의 객관적 가치에 대해 평가하더라도 감정평가사의 판단과 시각 등에 따라 조금씩 차이가 생기기 마련이다. 감정평가사는 토지가치에 대해 평가할 때 어떠한 가치가 객관적 가치이고 어떠한 가치가 주관적 가치인지 또는 토지의 가치 중 어떤 부분이 공공개발계획에서 비롯되어 추가된 가치인지를 판별해내야 한다. 이를 위한 기준들이 마련되어 있지만 모든 경우에 대해서 기준이 존재하기 힘들기 때문에 감정평가사의 판단에 따라 그 가치에 대한 평가가 달라질 수 있다.21)
이를 반영하기 위해 본 모형에서 감정평가사는 객관적 가치 V에 확률변수인 오차 ϵ을 더한 V + ϵ을 보상액으로 제시한다고 가정해 보자. 그리고 조정의 단계를 거치게 되면 오차는 사라지고 객관적 가치 V가 보상액으로 지급된다고 가정한다. 이러한 가정들하에서 게임의 균형을 살펴보자.
피수용자는 최하부 게임에서 자신의 토지가치 V보다 크거나 같은 값이 제시되면 제시액을 수락하고 그렇지 않으면 거부하는 전략이 최적이다. 그리고 감정평가사 역시 게임의 결과와 상관없이 동일한 수수료를 받는다면 피수용자의 전략에 상관없이 자신의 평가액 V + ϵ을 제시할 것이다. 따라서 이 게임의 결과는 ϵ의 값에 달려 있다. 만약 오차 ϵ이 0보다 크거나 같다면, 즉 토지가치를 과대평가한다면 피수용자는 평가자의 제시액을 받아들일 것이고, 반대로 과소평가한다면 피수용자는 제시액을 거부할 것이다. 따라서 평가에 있어서 생기는 ϵ의 값에 따라서 예상되는 게임의 균형은 달라지게 된다. ϵ의 값이 양의 값으로 커질수록 과다보상의 문제가 더 커지게 되고 반대로 음의 값을 가질수록 보상액에 따른 사회적 갈등을 유발시키게 된다. 이는 과다보상의 문제와 보상 갈등 문제 등의 시각에서 보았을 때 ϵ의 기댓값 E[ϵ]과 분산 Var[ϵ]이 모두 0에 가까울수록 정당보상이라는 본래 목적에 가까워진다고 할 수 있다. 따라서 정당보상액과 차이가 많은 보상액이 책정되도록 하는 유인체계를 개선하기 위해 감정평가사로 하여금 보상액을 산정토록 한 현재의 제도가 보다 효과적으로 그 기능을 발휘하기 위해서는 ϵ의 기댓값 E[ϵ]과 분산 Var[ϵ]이 모두 0에 근접할 수 있도록 지속적인 노력과 제도적인 뒷받침이 필요하다.
<Table 1>에 따르면, 감정평가업무를 담당할 업체를 시행자가 선정하였는지 주민추천을 통해 선정하였는지에 따라 평가액의 차이가 크다는 것을 알 수 있다. 사업시행자가 선정한 감정평가업체 간에는 평가액이 상당히 근소하여 예로 든 58개 사업지구 중 평가액의 격차가 1% 이내인 경우가 약 65%에 달한다는 것을 보여준다. 그리고 그 격차가 5% 이내인 경우는 90%가 넘는다. 반면, 시행자가 선정한 감정평가업체의 평가액과 주민이 추천하여 선정된 감정평가업체의 평가액은 그 격차가 상당하다. 이는 앞서 정의했던 평가오차의 분포가 감정평가업체 선정주체의 영향을 받는다는 점을 의미한다. 이를 바탕으로 보았을 때 현실에서는 ϵ의 기댓값이 0이라고 보기에는 무리가 있다.
Source: Korea Independent Commission Against Corruption, 2007. 12.
또한 시행자 측에서 선정한 감정평가 업체 간의 격차가 상당히 적다는 점은 이들 평가업체들의 평가오차값들이 상호간에 독립적이지 않을 수 있다는 점을 보여주고 있다. 따라서 정책적, 제도적인 개선을 통해 오차의 기댓값이 0에 가깝도록 하고 그 오차값들도 평가업체들 간에 서로 독립적일 수 있도록 만들 필요가 있다. 다음 절에서는 이를 위한 구체적인 개선방안을 모색하고 있다.
공공수용제도와 관련하여 달성해야 할 정책목표는 법에서 정하고 있는 정당보상액에 근접하게 수용 보상액을 책정해야 하는 점과 보상과 관련한 사회적 갈등을 최소화해야 한다는 점이다. 이 두 가지 목표는 상당히 연관되어 있다. 공공수용과정에서 있어서 산정되는 보상액에 대한 기준이 불명확하여 수용에 관련된 당사자들의 자의적인 노력이나 분쟁 등에 의해 보상액이 달라질 가능성이 있다면 보상과 관련한 갈등은 지속될 것이다. 반대로 수용에 따른 보상액 산정의 기준이 명확하여 수용 당사자들의 노력과는 상관없이 객관적 가치에 대한 정당보상액으로 보상액이 책정된다면 이와 관련한 분쟁이나 갈등도 줄어들게 될 것이다.22)
앞서 살펴본 바와 같이 정당보상액 산정을 위해서는 이해관계를 벗어난 평가자의 중립적이고 정확한 평가가 매우 중요하다. 본 장에서는 평가자의 공정한 평가를 보장하기 위해 실시되고 있는 현 제도가 그 기능을 충분히 수행하고 있는지 그리고 만약 그렇지 못하다면 이를 개선하기 위해서는 어떤 방안이 있는지 살펴보고자 한다.
평가자의 중립적이고 정확한 평가를 위해서는 우선 다음의 두 조건이 만족되어야 한다.
즉, 평가에 대한 오차가 편향되지 않아야 하고 오차의 범위도 최소화되어야 한다.
현행 제도에서는 보상액을 산정할 때 복수의 평가자로 하여금 평가를 내리게 하고 이들 평가액의 산술평균을 내는 방식을 채택하고 있다.23) 이러한 제도는 보상액 산정오차의 범위를 줄이기 위해서 효과적일 수 있다. 다만, 이 같은 제도가 효과를 충분히 발휘하기 위해서는 평가자 간의 공분산이 낮은 값을 가져야 한다. 다음의 식을 보자.
여기서 xi는 평가자 i의 평가액이고, ϵi는 xi의 평가오차이다. 만약 Var(ϵ1) = Var(ϵ2) = ϵ > 0이라면 두 평가오차의 공분산 Cov(ϵ1, ϵ2)의 값이 낮을수록 평균값의 평가오차가 줄어든다. 극단적으로 두 평가오차 간의 공분산이 0이라면 산술평균의 평가오차는 단독으로 평가액을 산정할 때보다 절반으로 줄어들게 된다. 하지만 두 오차 사이의 상관계수가 1이어서 공분산값 Cov(ϵ1, ϵ2)이 Var(ϵ)과 같아진다면 산술평균의 평가오차는 단독으로 평가액을 산정할 때와 같아진다. 따라서 평가오차를 줄이기 위해 복수평가액의 산술평균으로 평가액을 산정하는 제도가 제 기능을 발휘하기 위해서는 평가오차 사이의 공분산이 낮은 값을 가져야 한다.
하지만 「토지보상법 시행규칙」 제17조를 살펴보면, 평가오차 사이의 공분산값을 높이도록 유도할 가능성이 있음을 알 수 있다. 「토지보상법 시행규칙」 제17조에서는 복수의 평가액 중 최고평가액과 최저평가액이 110%를 초과하는 경우 재평가를 요구해야 하고 해당 평가자에 대해 국토해양부 장관은 평가과정에 대한 별도의 조사를 하도록 되어 있다. 이는 평가에 있어서 주관적인 변수에 의해 평가액이 편향되는 것을 방지하기 위한 장치이다. 즉, E(ϵ) = 0에 근접하기 위해 도입된 제도라 볼 수 있다. 만약 복수의 평가자들이 상호 간에 평가에 대한 정보교환이 불가능하고 독립적으로 평가를 진행한다고 가정하면 「토지보상법 시행규칙」 제16조와 제17조에서 의도하는 바가 서로 상충하지 않는다. 하지만 시행규칙 제17조의 규정하에서 평가자들은 독립적으로 평가액을 산정했을 시 생길 수 있는 처벌의 가능성에 대해서 조심하지 않을 수 없다. 따라서 평가자들은 서로의 평가정보를 공유하여 평가오차 간 차이를 줄이려고 노력할 유인이 생겨난다. 이는 결과적으로 평가액 간의 공분산을 크게 만들고 극단적으로는 평가오차 간의 상관계수가 1에 가깝도록 만들 수 있다. 또한 평가자 간에 평가액에 대한 정보 교환이 활발히 일어나는 경우는 E(ϵ) = 0에 근접하고자 하는 본래 목표를 달성하기 힘들다. 평가액이 편향되었다고 하더라도 사전적으로 평가자 간 정보 교환 등을 통해 평가액 간의 차이가 크지 않도록 자체적으로 조정을 할 것이고 이때 다른 평가액들도 함께 편향되게 정해질 개연성도 충분히 있다.
따라서 「토지보상법 시행규칙」 제17조에서 규정하고 있는 재평가에 대한 기준은, 「토지보상법 시행규칙」 제16조에서 정하고 있는, 산술평균하여 평가액을 산정하는 제도의 본래 취지에 반하는 기능을 할 가능성이 있다. 즉, 두 규칙이 양립함에 따라 E(ϵ) = 0이라는 목표를 제대로 달성하지 못하면서 동시에 Var(ϵ)을 줄이지도 못하는 결과를 가져올 수 있다.
그러므로 Var(ϵ)을 줄이면서도 E(ϵ)이 편향됨이 없이 0에 가까이 갈 수 있도록 제도를 개선할 필요가 있다. 이를 위해서는 평가오차를 줄임과 동시에 E(ϵ)의 편향됨을 줄일 수 있는 제도가 필요하다. 이하에서는 이러한 논의를 바탕으로 관련 정책의 개선방향을 모색해 보도록 한다.
평가의 편향을 줄이기 위해서는, 첫 번째로 평가와 관련된 기준을 보다 명확하게 할 필요가 있다. 현재 관련 법규에서는 평가 관련 기준에 대하여 원칙적인 부분을 위주로 규정하고 있고 보다 자세한 기준들에 대해서는 감정평가협회에서 만든 감정평가지침 등에 정리되어 있다. 하지만 이러한 지침은 자율적으로 만들어진 규정으로 실제 감정평가 시 반드시 따라야 할 강제성은 없다. 감정평가의 편향을 최소화하기 위해서는 객관적 기준 마련이 가능한 부분에 대해서 정부 주도하에 구체적인 지침을 마련할 필요가 있다. 감정평가협회 차원에서 마련된 지침과 기존의 감정평가사례 등의 자료를 참고하여 강제성이 부여된 지침이 마련된다면 감정평가에서의 편향을 줄이고 이를 통해 보상액 산정 관련 갈등을 줄이는 데 도움을 줄 수 있을 것이다.
그리고 두 번째로, 명시적이고 객관적인 기준이 마련된 후에는 감정평가액 산정과정이 지침에 맞게 수행되었는지에 대한 검증과정도 강화될 필요가 있다. 현재 보상평가의 공정성을 제고하기 위해 감정평가협회에서 자체적으로 감정평가 업무에 대한 공적심사제도가 운영되고 있다. 하지만 이 역시 자율적으로 운영되고 있으며 그 절차에 대한 강제적인 규정이 없다. 그러므로 많은 경우 이러한 심사절차를 거치지 않고 감정평가액이 산정되고 있다. 따라서 정부 주도하에 마련된 지침에 따라 감정평가가 진행되었는 지를 보다 공적인 위치에서 검증하기 위해 관련 전문가들을 중심으로 심사위원회를 구성하고 심사절차를 의무화하는 방법도 고려해 볼 필요가 있다. 이때 공공사업을 추진하는 정부부처가 심사위원회의 업무에 영향을 미치지 못하도록 차단하는 것이 중요하다. 만약 그렇지 못하다면 앞서 살펴보았던 권한위임모형이 제대로 작동하지 못하게 되고 결국 정당 보상액과 차이가 큰 보상액이 산정될 우려가 있다. 따라서 공공사업에 대한 이해 관계가 없는 전문가들을 중심으로 심사위원회를 구성하기 위한 방안에 대해서도 지속적인 고민이 필요하다.
세 번째로, 공공사업 추진에 따른 해당지역 공시지가 변동에 대한 보다 구체적인 연구가 필요하다. 현재 평가액 산정시 공시지가를 기준으로 당해 토지 이용계획, 지가변동률, 생산자물가상승률 등을 참작하여 적정 가격을 산정한다.24) 따라서 개발이익의 배제라는 원칙을 달성하기 위해서는 평가액 산정의 기준이 되는 공시지가에 개발이익이 어느 정도 반영되어 있는지 파악할 필요가 있다. 개발 계획이 진행됨에 따라 해당 토지의 가치는 변화하고 이러한 가치의 변화는 공시지가에 반영된다. 그러므로 공공사업에 의해 공시지가가 어느 시점부터 어느 정도 영향을 받았는지를 정확하게 파악할수록 평가오차의 분산을 줄일 수 있게 되고 궁극적으로 정당보상의 원칙에 더 근접할 수 있을 것이다. 따라서 공공사업에 따른 공시지가의 변동에 대한 보다 체계적인 연구가 지속적으로 이루어질 필요가 있다. 이 같은 연구는 보상액 산정에서의 가격보정작업에 대한 기준을 구체화하기 위한 발판이 될 수 있다는 점에서 의의가 있다.
지금까지 평가액 산정 권한을 제3자인 감정평가사에게 위임하는 현행 제도에서 수용 보상액이 정당보상액에 근접하도록 하기 위한 방안들을 모색해 보았다. 살펴본 바와 같이 권한위임제도가 본래의 취지에 맞게 성공적으로 운영되기 위해서는 권한을 위임받은 감정평가사가 수용자나 피수용자의 이해관계와는 상관없이 객관적이고 독립적으로 업무를 수행하도록 제도적으로 보장하는 것이 매우 중요하다. 이를 위해서 보상액 산정과 관련된 업무와 절차에 대해 객관적이고 공식적인 기준을 확대하고 이를 지속적으로 보완해 나가는 일이 필요하다. 이러한 기준들이 명확해질수록 보상과 관련된 분쟁과 갈등이 줄어들게 될 것이기 때문이다.
또한 이러한 제도 개선과 더불어 장기적으로 감정평가업무의 공정성과 독립성을 향상시키기 위한 지속적인 연구가 필요하다. 감정평가업무의 특성상 공식적인 지침의 제정 및 개선만으로는 평가업무에 대한 모든 사항을 아우르기 힘들다. 따라서 정당보상의 정의에서부터 현실에서의 적용방식에 이르기까지 다양한 학문 분야에서의 지속적인 연구가 절실하다.
본 연구에서는 토지수용과 관련한 보상액 산정과정에 있어서 관련 당사자들의 이해구조에 대해 게임이론모형을 통하여 살펴보았다. 이를 통해 공공사업을 추진하는 수용자와 토지를 수용당하는 피수용자 모두가 법에서 정하는 정당보상액에 비해서 많은 금액을 보상액으로 책정하고자 하는 유인이 존재할 수 있음을 보였다. 피수용자가 자신이 소유한 토지에 대한 보상액을 조금이라도 더 높이려는 유인이 존재하는 것은 자명하다. 그와 더불어 수용자는 제시한 보상액에 대해서 피수용자가 거부를 하고 갈등과 분쟁을 일으키는 경우 추진하는 공공사업이 지연되어 막대한 피해를 입을 수 있기 때문에 정당보상액에 비해 많은 금액을 보상금으로 지급하고서라도 사업 지연을 막고자 하는 유인이 존재할 수 있음을 살펴보았다. 또한 이와 더불어 피수용자는 자신의 보상금을 높이기 위해 공공수용에 대해 전략적으로 갈등을 일으킬 유인이 존재함을 보였다.
과다보상 유인을 줄이고 전략적 갈등 유발 유인을 줄이기 위해서는 수용자와 피수용자가 가지는 인센티브가 보상액 산정에 미치는 영향을 최소화할 필요가 있다. 이를 위한 방안으로 본 연구에서는 권한위임모형을 소개하고 있다. 우선 보상액 산정과정을 수용자와 피수용자의 인센티브로부터 독립시킴으로써 정당보상을 달성하고 사전적으로 기대할 수 있는 전략적 갈등 수준이 더 낮은 이상적인 권한위임모형을 제시하였다. 그리고 현실에서 이러한 권한위임을 이루는 수단으로서 감정평가제도를 주목하고 있다. 해당 토지의 가치에 대한 전문적인 평가를 하는 전문자격사의 역할뿐 아니라 과다보상의 인센티브를 차단하는 권한위임 수단으로서도 감정평가제도는 중요한 의미를 가질 수 있다.
따라서 현재의 감정평가제도가 권한위임수단으로서의 역할을 보다 효과적으로 수행할 수 있도록 제도를 개선할 필요가 있다. 즉, 감정평가가 수용자나 피수용자의 인센티브에 영향을 받지 않고 독립적이고 객관적으로 이루어지도록 지속적인 노력이 필요하다. 이를 위해 본 연구에서는 감정평가기준이나 감정평가에 대한 검증절차를 보다 공식화하고 객관화할 필요가 있음을 지적하고 있다. 또한 감정평가방법론 연구, 특히 개발이익의 정도와 생성시기 등을 파악하기 위한 연구 등을 지속적으로 진행해야 할 필요성도 제기하고 있다. 이러한 노력을 통해서 감정평가업무가 보상액 관련 인센티브에서 완전히 독립적일 수 있을 때 정당보상과 전략적 갈등의 감소를 이룰 수 있을 것이다.
<명제 1 증명>
최하부 게임에서 피수용자는 x ≥ V이면 제시 보상액을 받아들이고 그렇지 않으면 거절하는 것이 피수용자의 최선의 전략이다. 차하부 게임에서 수용자는 x = V만큼 제시하는 것이 최선의 전략이다. 따라서 부분게임 완전균형의 결과는 x* = V이고, 제시된 x*를 피수용자가 받아들이는 것이다. (증명 끝)
<명제 2 증명>
수용자의 최적 선택을 위한 일계미분조건인 식 (3-6)의 x값에 EV를 대입하면 가정 3에 의해 다음의 부등식이 성립한다.
수용자의 최적 선택 문제에서 이계미분조건인 식 (3-7)에 의해 x값이 커질수록 일계미분식의 값은 줄어든다. 따라서 x값이 EV보다 클 때 일계미분조건을 만족하게 된다. (증명 끝)
<명제 4 증명>
(필요조건 증명) 만약 어떤 V값에 대해서 조건 1이 성립되지 않는다면, 그 V값을 토지가치로 가지는 피수용자는 반발 수준으로  가 아닌 다른 값을 선택할 것이다. 그러므로 반발 수준이
가 아닌 다른 값을 선택할 것이다. 그러므로 반발 수준이  인 공용균형은 존재하지 않는다.
인 공용균형은 존재하지 않는다.
(충분조건 증명)  가 조건 1을 만족시킨다고 하자. 주어진 제시액에 대해서 피수용자의 의사는 당연히 제시액을 수락했을 때와 거절했을 때의 보수를 비교하여 결정된다.
그리고 보상금을 제시하는 수용자는 피수용자의 반발수준에 따라 피수용자의 토지가치 V에 대한 믿음(belief)을 형성하고 이에 따른 최적의 제시액을 결정한다. 만약 피수용자의 반발 수준과 상관없이 수용자가 피수용자의 토지가치 V에 대해 가지는 믿음의 분포가 V의 분포와 일치하는 경우 피수용자의 반발 수준 θ에 따른 최적 제시액은 앞선 식 (4-2)에서 정의한 x*(θ)이다. 수용자가 x*(θ)를 제시하는 경우 피수용자는 반발 정도를 결정할 때 자신의 반발 정도에 따른 수용자의 제시액 x*(θ)를 고려하므로 그 제시액을 수락하는 게 좋을지 거절하는 게 좋을지 미리 알고 있다. 즉, 피수용자는 자신의 보상을 예상하고 최선의 반발 수준 θ를 정한다. 조건 1에 의해 모든 V에 대해서 최선의 반발 수준이
가 조건 1을 만족시킨다고 하자. 주어진 제시액에 대해서 피수용자의 의사는 당연히 제시액을 수락했을 때와 거절했을 때의 보수를 비교하여 결정된다.
그리고 보상금을 제시하는 수용자는 피수용자의 반발수준에 따라 피수용자의 토지가치 V에 대한 믿음(belief)을 형성하고 이에 따른 최적의 제시액을 결정한다. 만약 피수용자의 반발 수준과 상관없이 수용자가 피수용자의 토지가치 V에 대해 가지는 믿음의 분포가 V의 분포와 일치하는 경우 피수용자의 반발 수준 θ에 따른 최적 제시액은 앞선 식 (4-2)에서 정의한 x*(θ)이다. 수용자가 x*(θ)를 제시하는 경우 피수용자는 반발 정도를 결정할 때 자신의 반발 정도에 따른 수용자의 제시액 x*(θ)를 고려하므로 그 제시액을 수락하는 게 좋을지 거절하는 게 좋을지 미리 알고 있다. 즉, 피수용자는 자신의 보상을 예상하고 최선의 반발 수준 θ를 정한다. 조건 1에 의해 모든 V에 대해서 최선의 반발 수준이  이므로 모든 종류의 피수용자는 최적의 반발 수준을
이므로 모든 종류의 피수용자는 최적의 반발 수준을  로 정하게 된다. 따라서 앞서 언급한 θ에 따른 수용자의 V 분포에 대한 믿음이 합리적(rational)이라고 할 수 있다. 이 같은 합리적인 믿음하에 수용자는 최선의 제시액 x*(θ)를 결정하고 피수용자는 이에 따라 최선의 반발 정도(
로 정하게 된다. 따라서 앞서 언급한 θ에 따른 수용자의 V 분포에 대한 믿음이 합리적(rational)이라고 할 수 있다. 이 같은 합리적인 믿음하에 수용자는 최선의 제시액 x*(θ)를 결정하고 피수용자는 이에 따라 최선의 반발 정도( )와 제시액 수락 여부를 결정하므로 반발 수준의
)와 제시액 수락 여부를 결정하므로 반발 수준의  인 공용균형은 존재한다. (증명 끝)
인 공용균형은 존재한다. (증명 끝)
본 논문은 기 발간된 『공공수용제도 개선방안 연구(Ⅰ): 수용보상에 관한 유인체계 분석 및 개선방안』(정책연구시리즈 2010-04, 한국개발연구원, 2010)의 주요 내용을 수정·보완한 것임.
국내의 대표적인 연구로는 정희남 외(2008), 지대식 외(2006), 신봉기(2005), 허강무(2008), 강교식(2006) 등이 있다. 이들은 대부분 토지보상과 관련하여 제도, 판례, 설문조사 등을 근거로 제도적·법학적인 논의를 주로 하고 있다는 점에서 본 연구와 차이가 있다. 경제학적인 논의를 중심으로 하는 본 연구의 특성상 이들 문헌에 대한 자세한 정리는 생략한다. 토지보상과 관련한 국내 문헌에 대해서는 정희남 외(2009)에 잘 정리되어 있다.
따라서 본 모형에서 정의하는 할인율 β는 개별 공공사업별로 그 특성을 감안하여 다른 값을 가진다는 점에서 일반적인 경제학 모형에서 실질이자율을 반영하여 정의하는 할인율과는 차이가 있다.
만약 피수용자가 토지를 영원히 소유한다고 가정하고 또한 토지로부터 얻는 가치가 매기 일정하다고 가정하자. 실질할인율 δ하에서 피수용자는 협상이 결렬되었을 경우 토지로부터 (1 − δ)V를 금번 기에 얻고 조정을 통해 받게 되는 정당보상금 V의 현재가치는 δV이므로 피수용자의 보수는 V가 된다.
피수용자의 토지가치 V는 피수용자가 수용자의 제시액을 수락할지 거부할지 결정하기 이전 어느 단계에서 실제값이 결정되든 게임의 결과에 영향을 미치지 않는다. 본 모형에서는 수용자가 보상액을 제시하기 이전, 즉 게임의 최초단계에서 피수용자가V의 실제값을 알게 된다고 가정한다.
앞의 2절에서는 토지가치에 주관적 가치가 없이 오직 객관적으로 확인 가능한 가치만 있었으므로 V와 EV가 동일한 값을 가졌고, 이 때문에 제2절의 게임에서는 피수용자의 보수에 δ가 포함될 필요가 없이 단순히 V라고 표시되었다.
정치적 이해관계, 공공개발주체의 이해관계를 비롯해서 다양한 이해관계가 공공사업의 추진 결정에 영향을 미칠 수 있지만 본 모형에서는 논의의 단순화를 위해 사회적 순편익을 감안하여 공공사업 추진을 결정하는 것으로 가정하고 있다.
피수용자가 제시액을 거부했을 시 최대로 얻을 수 있는 보수는 V에 따라 증가하여 V를 가진 피수용자가 가장 큰 보수를 얻는다는 점은 the envelope theorem과 식 (4-1)을 통해 보였다. 따라서 V를 가진 피수용자가 제시액을 거부했을 시 최대로 얻을 수 있는 보수를 보상액으로 제시하면 모두가 이를 수락하게 된다.
고정 보수하에서 평가자는 토지가치 V를 보상액으로 제시한다는 가정에 큰 무리가 없지만, 이를 더욱 명확히 하기 위해서 평가자가 토지가치를 V만큼 제시하지 않을 경우 정부당국에 의해 적발될 확률이 양의 값으로 존재하고 이에 대한 처벌이 존재한다고 가정할 수도 있다.
조정자에 대한 수수료를 수용자가 부담함에 따라 권한위임모형에서 수용자의 균형보수는 이전 모형에서의 균형보수에 비해 적다. 따라서 권한위임을 할지 아니면 수용자가 보상액을 산정할지에 대한 결정을 수용자가 직접 할 경우는 권한위임모형이 실제로 이루어지기 힘들 수 있다. 본 논의에서는 권한위임이라는 제도도입 결정을 수용자가 아닌 정책당국에서 사전적으로 결정하는 것으로 가정하고 있다. 이는 제도도입에 대한 결정을 수용당사자가 아닌 정부가 결정한다는 점에서 현실적이다. 본 연구도 정당보상 달성을 위한 제도 개선책을 모색한다는 점에서 이러한 가정은 합당하다고 할 수 있다.
(1996). The Political Economy of Taking and Just Compensation. Public Choice, 89, 267-282, https://doi.org/10.1007/BF00159359.