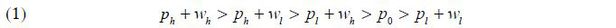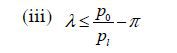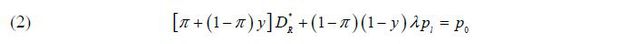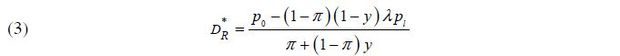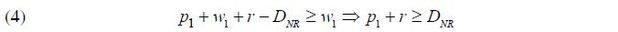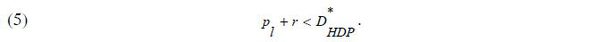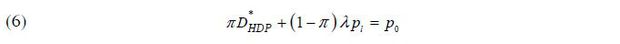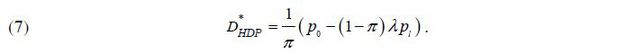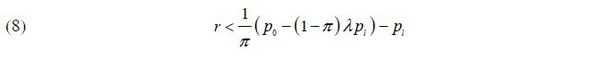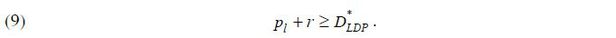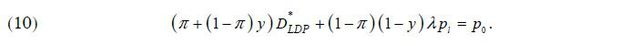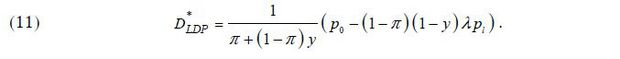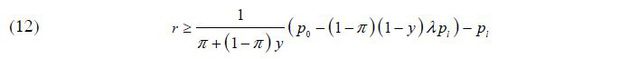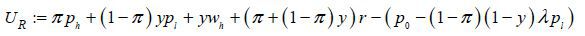The Effects of Non-Recourse Mortgages on Default Risks and Households’ Surplus†
Abstract
We study whether a default option attached to non-recourse mortgages improves borrowers’ surplus from mortgage financing. By defaulting on mortgage debt, borrowers can save their non-collateralized income from being foreclosed. In exchange, borrowers must forgo non-monetary surplus from retaining any collateral. Banks may charge a high mortgage rate due to increased default rates. We find that the interest rate of non-recourse mortgage decreases with the borrower’s surplus from home ownership. Moreover, non-recourse mortgages benefit only borrowers who deem housing property as an investment asset. Hence, the transition to a non-recourse mortgage is detrimental to welfare if the borrower enjoys a large surplus from home ownership. Although the borrower privately knows how much surplus she enjoys from home ownership, a menu of non-recourse mortgage contracts may exist, yielding a separating equilibrium without information rent.
Keywords
Non-recourse Mortgage, Strategic Default, Adverse Selection
JEL Code
D82, G18, G21
I. Introduction
Having observed the rapid increase in household debt in Korea, policy practitioners have launched numerous measures to resolve the problems associated with household economies and their ballooning levels of debt. One of these measures was to introduce non-recourse mortgages, by which lending banks are not allowed to foreclose on borrowers’ non-collateralized income to recover their losses. For instance, the Didimdol loan program of public mortgages funded by the National Housing and Urban Fund (NHUF) has offered non-recourse mortgage product to low-income households since 2015. The Financial Services Commission (FSC) also encouraged other government-run mortgage enterprises (such as the Korea Housing Finance Corporation (HF)) as well as private banks to sell non-recourse mortgage products.1
Obviously, these non-recourse mortgage products were introduced to protect household income from being used to meet possible hefty repayment obligations during economic downtowns. In the mortgage markets in Korea, banks have sold recourse mortgage products which guarantee lenders recourse to borrowers’ future income streams in the event of a default on their mortgage repayment. However, under the alternative non-recourse mortgage contracts, borrowers can decide to forgo nothing but the collaterals of the mortgages to the lending banks. Therefore, the borrowers preserve non-collateralized income to pay living expenses, even during times of economic distress.
Nevertheless, determining whether or not this provision of a default option is always better off for household borrowers is not always clear. Lifting the obligation to repay the outstanding debt will surely improve households’ surplus ex post amounts when recessions hit household economies. To the lending banks, however, less liquidation will increase the risk of default in the mortgage business. Out of fear of losses during economic downtowns, lending banks may charge a high risk premium to household borrowers. As a result, introducing non-recourse mortgages may increase the costs of mortgage financing, which may in fact make borrowers worse off (Bang, 2015).
Therefore, a careful examination is required of the effects of non-recourse mortgage contracts before they are introduced into the market. Particularly, borrowers may strategically exercise the default option even if they have a sufficient amount of income to repay the outstanding debt, which may result in welfare losses due to the costly liquidation process. Moreover, speculative investors may abuse this default option as a means of reducing their exposure to investment losses. In such cases, the introduction of non-recourse mortgages may only subsidize speculators. Given that speculation in the housing market has always been an important policy consideration in Korea, investigations of the links between non-recourse mortgage instruments and borrowers' motives for home purchases are necessary.
Since the pioneering work of Vandell (1978), the economic impacts of alternative mortgage instruments (including non-recourse mortgages) on borrowers’ repayment decisions has attracted the attention of many academic researchers. Particularly, the literature expanded rapidly after the U.S. subprime mortgage crisis of 2007-2009. For instance, Campbell (2012) compared the U.S. and Europe with regard to differences in mortgage market structures in terms of various economic and institutional aspects. Hatchondo et al. (2015) proposed LTV limits as a policy instrument to complement traditional recourse mortgages. Kim (2015) analyzed and simulated how households' optimal default decisions change over time with their selection to finance home purchases, such as with non-recourse mortgages and unsecured loans. Lastly, Piskorski and Tchistyi (2010) solve an optimal mortgage design problem in a general continuous-time dynamic contract framework.
There are also empirical works related to alternative mortgage instruments. For instance, Ghent and Kudlyak (2011) and Corbae and Quintin (2010) both found that non-recourse mortgages yield higher default rates than recourse mortgages. Using survey data, Guiso et al. (2013) found that non-financial factors, such as fairness and morality, associated with households may determine their decisions strategically to default on their mortgages. Cocco (2013) used U.K. household panel data to estimate that non-recourse mortgage products can be useful for households to smooth their future consumption patterns.
However, despite its importance, there is scant literature found in Korea on the impacts of non-recourse mortgages on household economies. To the best of the author’s knowledge, there are few theoretical studies of a strategic link between household demand for houses and their decisions regarding the fulfillment of their repayment obligations. Without a careful examination of the economic impacts of relevant policies, no one can appropriately predict the ramifications of introducing non-recourse mortgage products. To address this problem, we present a simple and stylized model to analyze why borrowers strategically default on their non-recourse mortgage debt. Specifically, we focus on how the default risk of non-recourse mortgage contracts varies with households’ purposes for buying housing.
In our model, a borrower purchases a house via mortgage financing, in which a lending bank collateralizes the purchased house. The borrower has two future sources of income in the future: capital gains from the collateralized house and non-collateralized labor income. Every individual bank competes with others to sell the mortgage to the borrower by offering certain mortgage repayment terms. If the household defaults on the debt, the lending bank forecloses and liquidates the collateral so as (partially) to recover its loss. We assume that the liquidation process incurs a loss of value from the collateral, which constitutes the welfare loss.
We consider two types of mortgage products in our model. With a recourse mortgage, if the household defaults on its mortgage, the lending bank will foreclose and make a claim to all of the borrower’s income, including non-collateralized income. However, under a non-recourse mortgage, the borrower can avoid her remaining mortgage debt by surrendering the collateralized property. By doing so, the borrower can preserve her non-collateralized labor income from going towards the outstanding debt. To capture the impact of non-recourse mortgages, we compare the borrower’s gains from mortgage financing for these two types of mortgage products.
A key assumption is that the borrower enjoys an additional non-monetary (and possibly subjective) surplus by retaining ownership of the property purchased via mortgage financing. This surplus can be obtained if the borrower fulfills her mortgage repayment. This additional surplus can be referred to as the value of living in the purchased house. For example, if the borrower gains a surplus of zero from homeownership, she views the housing property merely as an investment asset for capital gains. On the other hand, if the borrower gains a high level of homeownership surplus, she views this housing property as a residence. Thus, this type of borrower is, if necessary, willing to repay the mortgage debt with her non-collateralized income.
We show that the probability of default in the case of a non-recourse mortgage decreases with the borrower’s surplus from repaying the mortgage debt.2 If the borrower’s homeownership surplus is relatively low, the mortgage repayment cost may outweigh the associated benefit. Given this low value of homeownership surplus, the concept of HDP equilibrium comes into play (where HDP stands for “high default probability”), in which the borrower retains non-collateralized income when the housing price decreases below the total amount of the mortgage debt. The banks charge high mortgage rates due to the increased default risk. In contrast, if the borrower’s homeownership surplus is relatively high, the benefit of repaying the mortgage will outweigh the cost. Given this high value of homeownership surplus, there exists LDP equilibrium (where LDP denotes “low default probability”), in which the borrower uses non-collateralized labor income to repay her mortgage debt fully. Accordingly, banks do not charge high mortgage rates because the default risk level does not increase compared to that under a recourse mortgage.
We also determine whether or not a transition to a non-recourse mortgage improves the borrower’s gains from mortgage financing. We find that there is a threshold of the borrower’s homeownership surplus such that the non-recourse mortgage improves the borrower’s gains if and only if the borrower’s homeownership surplus is under that threshold. In such a case, the default option enabling the borrower to avoid the repayment obligation presents a high value to the borrower when the value of the homeownership surplus is low. Meanwhile, the increased interest rate may harm the borrower’s gains from mortgage financing. Given a high value of the default option, the borrower will realize higher gains with a non-recourse mortgage, although she faces a high interest rate compared to the recourse mortgage product. Otherwise, the borrower will be worse off due to the increased cost of borrowing, whereas the default option presents a low value.
Similarly, we find that the transition to a non-recourse mortgage improves welfare if and only if the borrower’s homeownership surplus is low. The total welfare is the borrower’s gains from mortgage financing minus the expected social cost from liquidation in the event of a default. Under a non-recourse mortgage, the increased default probability in the state of HDP equilibrium yields a greater welfare loss due to the costly liquidation of the foreclosed property. As explained above, the value of the default option is decreasing in the event of a borrower homeownership surplus. Therefore, a non-recourse mortgage improves social welfare if and only if the borrower’s homeownership surplus is sufficiently low and, therefore, the value of the borrower’s default option is very high.
In the main model, the borrower’s surplus from retaining homeownership is assumed to be publicly known by the banks. However, it may be more realistic to assume that such homeownership surplus is private information available only to the borrower. Indeed, banks may not be able fully to verify whether the borrower buys housing as a residence or for speculative purposes. To enhance fully relevance of our analysis, we augment our model by introducing informational asymmetry with regard to each borrower’s homeownership surplus.
We analyze whether or not the adverse selection problem will make the borrower worse off compared to complete information.3 We find that there may be a separating equilibrium by which the borrower realizes the same gains as she would under a scenario of complete information. Consider the borrower with a high homeownership surplus first, who receives low repayment terms in equilibrium. If the housing price is lower than the mortgage debt, this type of the borrower would rather use her non-collateralized income to fulfill her repayment obligations. Because such borrowers rarely exercise the default option, they prefer a mortgage product that offers the lowest mortgage repayment terms, leading to the highest residual income after repayment. Next, consider the borrower with a low homeownership surplus, who receives the high repayment terms by reporting her true type in equilibrium. If the homeownership surplus is not too low, this type of the borrower will actively exercise her default option to prevent her non-collateralized income from being foreclosed upon compared to the other type of borrower. If the borrower lies about her type, she will be offered low repayment terms to an extent such that she needs not exercise the default option. Put differently, this type of borrower will endogenously surrender her default option by mimicking the other type. However, the equilibrium repayment terms offered by competitive banks are not hefty enough for the borrower to misreport her type for the sake of low repayment terms. Therefore, it is optimal for the borrower to report her type truthfully.
The remainder of the paper proceeds as follows. Section 2 presents our model. In Section 3, we discuss equilibrium under the recourse mortgage contract as a benchmark of our main analysis. In Section 4, we study the strategic interaction between borrowers and banks under non-recourse mortgage contracts and derive related policy implications. In Section 5, we conduct the equilibrium analysis under asymmetric information regarding borrowers' surplus amounts from retaining homeownership. Section 6 concludes the paper.
II. Model
Consider a two-period (t = 0,1 ) economy with a household and a number of competitive banks. When the game begins in t = 0 , there is a house available for sale in this economy. The borrower can purchase this house at a price of p0 > 0 . We assume that the household has zero initial wealth such that the house is unaffordable without external financing. However, the borrower can buy the house by borrowing from one of the banks via mortgage financing. Specifically, the borrower can borrow money p0 from a bank by collateralizing the house she would like to purchase. In return, she is obliged to repay the mortgage debt with an amount D > 0 in t = 1 .4 If the borrower does not repay her mortgage, the ownership of the collateralized house is transferred to the lending bank. The bank liquidates the collateral to recover (partially) the loss from the default. We assume that banks in the mortgage market compete á la Bertrand with regard to selling mortgage products such that the repayment term D is determined to break the lending bank even.
After purchasing the house, the borrower can repay the mortgage debt by spending either capital gains or labor income realized in t = 1. Specifically, the household can realize a capital gain (or loss) from the purchased house in t = 0 : the house price in t = 1 , denoted by p1, may increase to ph > p0 with probability π ∈ (0,1) or decrease to pl < p0 with probability 1 − π. In addition, the borrower gets a separate labor income w1 in t = 1. We assumed that w1 is a binary random variable such that the household gains high labor income ( w1 = wh ) with probability y ∈ (0, 1) and low labor income (w1 = wl) with probability 1 − y, where wh > wl. We also assume that w1 is mutually independent of p1.
A key assumption in this model is that the household enjoys an additional surplus from retaining ownership of the purchased house. Specifically, we assume that if the borrower fully repays her mortgage debt, she gains a non-monetary surplus r > 0 in t = 1. In contrast, if the household defaults on her mortgage debt, the collateralized house will be foreclosed and thus the borrower cannot gain r. We can interpret r > 0 as the benefit the borrower enjoys from having her own residential unit. If r is high, the household then has a strong incentive to repay her mortgage debt. In contrast, a borrower with a low r can be interpreted as one who deems the house as an investment asset rather than a residential unit. In Sections 4 and 5 below, we discuss in more detail how this non-contractible surplus from homeownership will influence the default decisions of borrowers.
If the borrower defaults on her debt, the lending bank liquidates the collateralized house (partially) to recover its loss. We assume that the liquidation process cases a loss. One can consider the loss of the transaction and the legal costs incurred when the ownership of the collateral is transferred to the lenders. A liquidation loss can be also incurred by the inefficient allocation of collateral due to a fire sale in the secondary market.5 Throughout, we assume that the bank retains λp1 at most by liquidating the collateral, where λ ∈ (0, 1).6 Furthermore, we assume the following:
Equation (1) can be interpreted as follows. If the borrower realizes capital gains (p1 = ph) in t = 1, she does not have to use her non-collateralized income w1 in order to fulfill her repayment obligation D . Under this assumption, the capital gains from the house price are the primary source of income to repay the mortgage debt. This setting also takes into account the possibility that when the borrower finances her home purchase, she may have to take on the risk of losing all of her income.
We consider two types of mortgage products initially as to whether or not lenders (banks in our model) have recourse against losses from their mortgage business. First, banks can offer a recourse mortgage contract, in which the borrower is obliged to fulfill her outstanding debt. Under this type of contract, the borrower’s labor income is foreclosed to be used to repay the mortgage debt when the borrower defaults on her debt. In other words, the household’s total income is collateralized by the lending bank. Second, banks can offer a non-recourse mortgage contract in which the borrower does not need to repay the outstanding debt after defaulting on her mortgage. Under this contract, the borrower can preserve all of her labor income in t = 1 by defaulting on her mortgage.
The game proceeds with the following timeline of actions:
1. In t = 0 , each competitive bank offers a mortgage contract with repayment term D to the household.
2. The household decides whether or not to sign a mortgage contract to finance the home purchase.
3. In t = 1, w1 and p1 are realized.
4. Under a non-recourse mortgage contract, the household decides whether to repay the mortgage or to default on it. Under a recourse mortgage, the household gains the residuals of its total income after repayment of the mortgage.
5. In the event of a default, the lending bank takes over and liquidates the collateralized house.
III. The Equilibrium under the Recourse Mortgages
As a benchmark, we initially characterize the state of equilibrium under a recourse mortgage, in which banks have recourse against losses incurred by borrower defaults on mortgage debt. This analysis will facilitate an understanding of the strategic interaction not only among competing banks but also between lending banks and borrowers.
We analyze how the mortgage repayment terms are determined in equilibrium. In our
model, a bank which offers a mortgage contract with the lowest repayment terms will
win the competition. Hence, the equilibrium repayment term, denoted as  , will make zero expected profit. For simplicity of our analysis, we assume the following:
, will make zero expected profit. For simplicity of our analysis, we assume the following:
Assumption 1.
Assumption 1-(ii) is introduced to normalize all sources of the future income in t = 1.
Under Assumption 1, there exists a repayment term D ∈ [p0, ph] which gives zero expected profit to the banks. Given this D , it follows from the equation (1) that the borrower may default on her mortgage
debt only given the state of the lowest income which occurs with probability (1 −
π) (1 − y). In this state, the bank liquidates the collateralized house to obtain λpl. In the other states, the lending bank expects to receive the full repayment with
probability π + (1 − π)y. Therefore, the repayment term  must be determined by the following indifference condition:
must be determined by the following indifference condition:
The left-hand side of equation (2) is the expected payoff from lending to the borrower, and the right-hand side is the total amount of money lent to the borrower. From equation (2), the equilibrium repayment term is determined as
The next proposition presents how equilibrium under the recourse mortgage contract is characterized.
Proposition 1.
Suppose the bank has recourse against losses incurred by the mortgage. In such a case,
there exists a unique equilibrium in which every bank offers repayment term 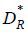 as determined by equation (3).
as determined by equation (3).
Proof.
From Assumption 1, 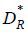 determined by equation (3) is the only repayment term by which the bank breaks even.
Suppose there exists an equilibrium state in which banks offer
determined by equation (3) is the only repayment term by which the bank breaks even.
Suppose there exists an equilibrium state in which banks offer 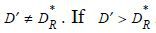 , an individual bank has an incentive to offer D ∈ (D',
, an individual bank has an incentive to offer D ∈ (D', 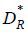 ). If D' <
). If D' < 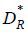 , lending to the borrower is unprofitable by the equation (2), so all banks will not
offer such a mortgage contract, a contradiction. Using the same logic, one can also
find that it is optimal for each individual bank to offer
, lending to the borrower is unprofitable by the equation (2), so all banks will not
offer such a mortgage contract, a contradiction. Using the same logic, one can also
find that it is optimal for each individual bank to offer 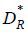 , given all other banks offer the same contract. Q.E.D.
, given all other banks offer the same contract. Q.E.D.
One noteworthy feature from Proposition 1 is that the equilibrium repayment term does not change with the borrower’s surplus from retaining homeownership r > 0, as the borrower’s labor income is subject to foreclosure under the recourse mortgage contract. In other words, the borrower cannot exercise her default option in order to preserve her labor income.
However, this does not necessarily mean that the borrower is worse off when the mortgage contract does not grant the default option. The foreclosure of future income in a poor state clearly harms the household’s welfare. In this regard, the household can set the labor income w1 apart for future consumption. However, giving recourse to the lender may increase the risk that the borrower is more likely to default on her mortgage debt. Thus, the lack of the default option may lower the default risk and thus the borrower can fund the home purchase more inexpensively. Due to this tradeoff of the default option, a careful examination of the value of the default option under a non-recourse mortgage contract is necessary.
IV. Equilibria under Non-Recourse Mortgages
In this section, we analyze how a borrower strategically exercises the default option under a non-recourse mortgage. By defaulting on her mortgage, the borrower can prevent her non-collateralized income from being foreclosed. However, the borrower must forgo any non-monetary surplus from retaining homeownership. Thus, the equilibrium mortgage repayment terms will be closely related to the borrower’s valuation of the default option.
Under a non-recourse mortgage, the benefit r > 0 from fulfilling the repayment obligation will determine the borrower’s default decision. Let DNR denote the repayment term under the non-recourse mortgage contract. Given the house price p1 and the labor income w1 , the borrower repays her mortgage debt if and only if
If the borrower fully repays her mortgage DNR , she gains net payoff (p1 + w1 − DNR) + r. If the household defaults on her mortgage debt, the collateralized house will be foreclosed but she can keep her labor income w1 away.
Equation (4) reveals the tradeoff of the mortgage debt repayment. If the borrower fully repays the mortgage debt, she will lose her non-collateralized income, which may otherwise have been used for her own consumption. In return, she enjoys the additional utility stemming from securing her place as a residence. If it is too costly for the household to repay DNR , then the household will default on the mortgage debt in order to prevent the labor income from being foreclosed.
Here, we characterize equilibria under a non-recourse mortgage contract. To this end, we assume the following:
Assumption 2. p0 ≤ πph + (1 − π)λpl
Under this assumption, there will be no equilibrium in which the repayment term exceeds ph. Therefore, we can focus on equilibrium where the borrower may (strategically) default on her mortgage debt only if the future price of the house is equal to pl. Indeed, it appears unrealistic to postulate that the borrower defaults on her mortgage debt even if she earns capital gains from her property.
There are two possibilities leading to the borrower’s default decision in equilibrium. First, there may exist a state of equilibrium in which the borrower chooses to default when her income in t = 1 is pl + wh.7 We label this equilibrium as the HDP type, which stands for “high default probability.” From equation (4), the borrower will default on her mortgage debt if and only if
Because pl + wh > pl, the borrower will surely go bankrupt in the state pl + wh = pl, which takes place with probability 1 − π. Thus, the equilibrium repayment term 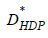 must satisfy the following zero-profit condition:
must satisfy the following zero-profit condition:
The house price goes up to ph with probability π, in which case the lending bank receives full repayment. In the state p1 = pl with probability 1 − π, however, the borrower defaults on her mortgage debt, in which case the lending bank
forecloses on the house and liquidates the collateral (partially) to recover its loss.
Because the equilibrium repayment term must allow the lending bank to break even,
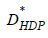 is determined as
is determined as
To support the borrower’s equilibrium default decision, 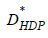 as determined by equation (7) must satisfy constraint (5), which yields the necessary
condition of r > 0 :
as determined by equation (7) must satisfy constraint (5), which yields the necessary
condition of r > 0 :
Equation (8) indicates that r > 0 should be sufficiently small. As discussed above, the borrower faces a tradeoff with regard to mortgage repayment. By repaying the mortgage debt, the borrower enjoys the homeownership surplus r > 0. However, if the housing price drops below the total mortgage debt, she may have to spend all or some of w1 to repay the outstanding debt. If the surplus from retaining homeownership is relatively low, she will strategically decide to default on her mortgage debt.
Next, we consider an alternative type of equilibrium in which the borrower fulfills her mortgage repayment obligation despite the fact that a capital loss occurs in t = 1. We label this equilibrium type as the LDP type, where LDP is an acronym for “low default probability.” In this equilibrium state, the borrower prefers repaying her mortgage when her income is pl + wh in t = 1. From equation (4), we have
As in the HDP equilibrium state, the borrower will repay her mortgage debt when her homeownership surplus is greater than the total mortgage repayment. Hence, the borrower defaults on her mortgage debt only if her total income in t = 1 is not high enough to fulfill her repayment obligation. Therefore, the repayment term will be determined by the following zero-profit condition:
From equation (10), we have
Because 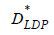 determined by (11) must satisfy the necessary condition (9), we have the following
condition pertaining to r > 0 :
determined by (11) must satisfy the necessary condition (9), we have the following
condition pertaining to r > 0 :
If the surplus from homeownership is high, the borrower does not have an incentive strategically to default on her mortgage debt. Thus, equation (12) means that LDP equilibrium can exist only if the borrower’s homeownership surplus is sufficiently high.
From equations (5)-(12), we can characterize HDR and LDR equilibria as follows:
Proposition 2.
Under a non-recourse mortgage contract, there exist 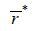 such that HDP equilibrium arises from
such that HDP equilibrium arises from 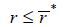 and LDP equilibrium arises from
and LDP equilibrium arises from 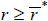 .8
.8
Proof.
First, we establish some of the technical results used in the proof. Define 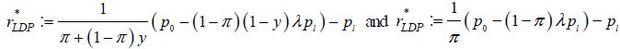 . One can easily show that
. One can easily show that 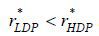 .
.
Next, let UHDP := πph + (1 − π)ypl + ywh + πr − (p0 − (1 − π)λpl) denote the borrower’s expected payoff under a non-recourse mortgage with repayment
term 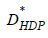 , and ULDP := πph + (1 − π)ypl + ywh + (π + (1 − π)y)r − (p0 − (1 − π)(1 − y)λpl) denote the borrower’s expected payoff under a non-recourse mortgage with
, and ULDP := πph + (1 − π)ypl + ywh + (π + (1 − π)y)r − (p0 − (1 − π)(1 − y)λpl) denote the borrower’s expected payoff under a non-recourse mortgage with 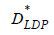 . One can then find that there exists
. One can then find that there exists 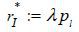 such that ULDP − UHDP > 0 if and only if
such that ULDP − UHDP > 0 if and only if  , Note from Assumption 1-(iii) that
, Note from Assumption 1-(iii) that 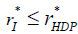
We will initially show that only HDP equilibrium can exist for every 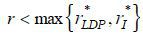 . Suppose to the contrary that LDP equilibrium exist for some
. Suppose to the contrary that LDP equilibrium exist for some 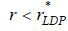 . Because banks compete a la Bertrand, the equilibrium repayment term must be
. Because banks compete a la Bertrand, the equilibrium repayment term must be 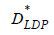 . However, we have
. However, we have 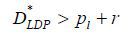 according to (12), a contradiction. Next, suppose
according to (12), a contradiction. Next, suppose 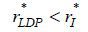 and that LDP equilibrium exists for some
and that LDP equilibrium exists for some 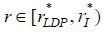 . From the definition of
. From the definition of 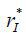 , a bank can profitably deviate by offering
, a bank can profitably deviate by offering 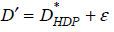 for a small case of ε > 0 such that the borrowers’ expected payoff from buying the mortgage at D' is strictly greater than ULDP, a contradiction.
for a small case of ε > 0 such that the borrowers’ expected payoff from buying the mortgage at D' is strictly greater than ULDP, a contradiction.
Next, we show that HDP equilibrium cannot exist for every 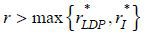 . Proceeding similarly to the previous argument, suppose to the contrary that HDP equilibrium exists for some
. Proceeding similarly to the previous argument, suppose to the contrary that HDP equilibrium exists for some 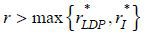 . In such a case, a bank can profitably deviate by offering mortgage rate D' =
. In such a case, a bank can profitably deviate by offering mortgage rate D' = 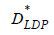 + ε for a sufficiently small ε ∈ ( 0, pl + r −
+ ε for a sufficiently small ε ∈ ( 0, pl + r − 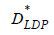 ) such that the borrower’s expected payoff from buying the mortgage at D' is strictly greater than UHDP , a contradiction.
) such that the borrower’s expected payoff from buying the mortgage at D' is strictly greater than UHDP , a contradiction.
Next, we prove that HDP equilibrium exists for all 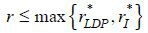 . To this end, first we show that it is optimal for the borrower to use the prescribed
equilibrium strategies in each state, given repayment term
. To this end, first we show that it is optimal for the borrower to use the prescribed
equilibrium strategies in each state, given repayment term 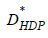 . Because any
. Because any 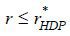 satisfies equation (8),
satisfies equation (8), 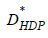 also satisfies the equation (5) for all
also satisfies the equation (5) for all 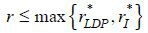 . Thus, it is optimal for the borrower to default on her mortgage if p1 + w1 = pl + wh. If p1 + w1 = pl, the borrower cannot repay
. Thus, it is optimal for the borrower to default on her mortgage if p1 + w1 = pl + wh. If p1 + w1 = pl, the borrower cannot repay 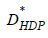 and thus goes bankrupt. If
and thus goes bankrupt. If 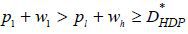 , the borrower then prefers to repay her mortgage. We show next that it is optimal
for banks to offer
, the borrower then prefers to repay her mortgage. We show next that it is optimal
for banks to offer 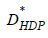 . If a bank offers repayment term
. If a bank offers repayment term 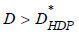 , the borrower will not buy the mortgage. If a bank offers repayment term
, the borrower will not buy the mortgage. If a bank offers repayment term 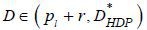 , the borrower will sell the mortgage but such a deal will generate a loss according
to equation (8). Suppose a bank offers repayment term
, the borrower will sell the mortgage but such a deal will generate a loss according
to equation (8). Suppose a bank offers repayment term 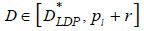 . If
. If 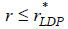 , such an offer will generate a loss for the bank according to equation (12). If r ≤
, such an offer will generate a loss for the bank according to equation (12). If r ≤ 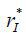 , the borrower will not buy the mortgage under this repayment term because the borrower’s
expected payoff with D is weakly lower than ULDP but ULDP − UHDP < 0. Lastly, a bank will realize a loss by offering D <
, the borrower will not buy the mortgage under this repayment term because the borrower’s
expected payoff with D is weakly lower than ULDP but ULDP − UHDP < 0. Lastly, a bank will realize a loss by offering D < 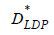 .
.
Lastly, we prove that LDP equilibrium exists for all 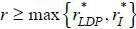 . Proceeding in a manner similar to the previous argument, one can show that it is
optimal for the borrower to utilize the prescribed equilibrium strategies in each
state given repayment term
. Proceeding in a manner similar to the previous argument, one can show that it is
optimal for the borrower to utilize the prescribed equilibrium strategies in each
state given repayment term 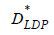 . Next, we show that it is optimal for banks to offer
. Next, we show that it is optimal for banks to offer 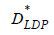 . If a bank deviates and offers
. If a bank deviates and offers 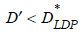 , it can attract the borrower but will make a loss by the equation (12). If a bank
offers
, it can attract the borrower but will make a loss by the equation (12). If a bank
offers 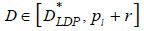 , it cannot sell the mortgage to the borrower. If a bank offers D' > pl + r and the borrower buys the mortgage under this repayment term, the borrower’s expected
payoff will be weakly less than UHDP . Because UHDP - ULDP ≤ 0 for all
, it cannot sell the mortgage to the borrower. If a bank offers D' > pl + r and the borrower buys the mortgage under this repayment term, the borrower’s expected
payoff will be weakly less than UHDP . Because UHDP - ULDP ≤ 0 for all 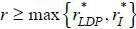 , the borrower will not buy the mortgage from the deviating bank, i.e., Q.E.D.
, the borrower will not buy the mortgage from the deviating bank, i.e., Q.E.D.
During the equilibrium characterization step, how the borrower values the default
option attached to a non-recourse mortgage is crucial. 9 Suppose the borrower enjoys a high level of homeownership surplus (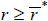 ). In this case, forgoing this surplus severely harms the borrower’s expected gains
from mortgage financing. Thus, the borrower is willing to fulfill her mortgage repayment
obligation even if it requires her to use her non-collateralized income. Because the
default risk remains unchanged compared to that in a recourse mortgage, the bank does
not charge a high mortgage rate to the borrower compared to the case of a recourse
mortgage.
). In this case, forgoing this surplus severely harms the borrower’s expected gains
from mortgage financing. Thus, the borrower is willing to fulfill her mortgage repayment
obligation even if it requires her to use her non-collateralized income. Because the
default risk remains unchanged compared to that in a recourse mortgage, the bank does
not charge a high mortgage rate to the borrower compared to the case of a recourse
mortgage.
Next, suppose the borrower’s homeownership surplus is relatively low (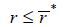 ). In this case, the borrower deems the housing property to be a financial asset rather
than a residence. If the housing price is lower than the mortgage debt, the borrower
will exercise the default option because the opportunity cost of default is not high.
Due to the increased default risk, the bank will charge a high mortgage rate to the
borrower. With a high repayment term, the borrower becomes even less willing to use
non-collateralized income to repay the mortgage. However, the Bertrand competition
among banks keeps the mortgage rate in the state of HDP equilibrium not overly high. Hence, the borrower chooses the mortgage contract with
). In this case, the borrower deems the housing property to be a financial asset rather
than a residence. If the housing price is lower than the mortgage debt, the borrower
will exercise the default option because the opportunity cost of default is not high.
Due to the increased default risk, the bank will charge a high mortgage rate to the
borrower. With a high repayment term, the borrower becomes even less willing to use
non-collateralized income to repay the mortgage. However, the Bertrand competition
among banks keeps the mortgage rate in the state of HDP equilibrium not overly high. Hence, the borrower chooses the mortgage contract with
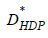 as opposed to other mortgage contracts with repayment terms lower than
as opposed to other mortgage contracts with repayment terms lower than 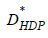 .
.
The equilibrium characterization in Proposition 2 also provides a hint pertaining to how the transition to a non-recourse mortgage affects the borrower’s gains from a mortgage. As presented in the following observation, a non-recourse mortgage indeed makes the borrower who buys housing property for speculative purposes better off.
Proposition 3.
There exists 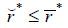 such that the borrower’s expected payoff is higher under a non-recourse mortgage than
under a recourse mortgage if
such that the borrower’s expected payoff is higher under a non-recourse mortgage than
under a recourse mortgage if 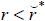 , the borrower’s expected payoff under a non-recourse mortgage is strictly lower than
otherwise if
, the borrower’s expected payoff under a non-recourse mortgage is strictly lower than
otherwise if 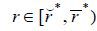 , while the borrower’s expected payoff does not change with alternative types of mortgage
products if
, while the borrower’s expected payoff does not change with alternative types of mortgage
products if 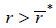 .
.
Proof.
Recall 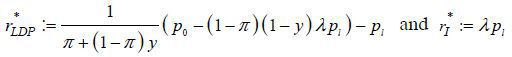 from the proof of Proposition 2. Let
from the proof of Proposition 2. Let
denote the borrower’s expected surplus under a recourse mortgage. According to equation
(3), one can easily find that UR = ULDP, 10 where ULDP is the expected surplus with repayment term 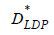 under a non-recourse mortgage.
under a non-recourse mortgage.
There are two possibilities, either 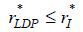 or
or 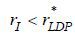 . Consider
. Consider 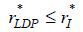 first. From the proof of Proposition 2, HDP equilibrium arises under a non-recourse mortgage if and only if
first. From the proof of Proposition 2, HDP equilibrium arises under a non-recourse mortgage if and only if 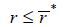 =
= 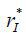 . According to the definition of
. According to the definition of 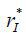 , we have UR − UHDP = ULDP − UHDP > 0 if and only if
, we have UR − UHDP = ULDP − UHDP > 0 if and only if 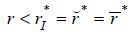 . Furthermore, UR − ULDP = ULDP − ULDP = 0 for all
. Furthermore, UR − ULDP = ULDP − ULDP = 0 for all 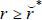 , where the inequality is strict if and only if
, where the inequality is strict if and only if 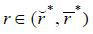 . Q.E.D.
. Q.E.D.
The key contribution of the non-recourse mortgage to the borrower’s gains from mortgage
financing is the default option. The value of the default option varies with the borrower’s
surplus from retaining homeownership. When the housing price falls below the repayment
term ex post, the cost of defaulting is r ≥ 0 , the borrower’s surplus from homeownership. The benefit of defaulting is the
retention of non-collateralized income. Thus, it is straightforward to consider that
the ex-post net benefit of the default option is a decrease in r . However, the increased probability of default leads to a high borrowing cost ex ante. If r is relatively low (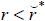 ), the benefit of the default option outweighs its total cost, indicating that a transition
to a non-recourse mortgage improves the borrower’s gains from mortgage financing.
If r is relatively high (
), the benefit of the default option outweighs its total cost, indicating that a transition
to a non-recourse mortgage improves the borrower’s gains from mortgage financing.
If r is relatively high (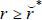 ), the non-recourse mortgage leads to an increase in the borrowing cost, which makes
the borrower worse off.11
), the non-recourse mortgage leads to an increase in the borrowing cost, which makes
the borrower worse off.11
Proposition 3 features a noteworthy policy implication: the introduction of a non-recourse mortgage may not always make households better off. Particularly, a non-recourse mortgage mainly benefits “speculative” homebuyers who use leverage with their investments in housing properties (i.e. those with low values of r ’s). In contrast, households buying houses for residential purposes (i.e., those with high values of r ) will take residual income into account after debt repayment as compared to post-default income. Therefore, these homebuyers prefer relatively low mortgage rates to the default option. From this perspective, the policymakers should carefully examine the characteristics of the beneficiaries of non-recourse mortgage products.
We conclude this section by comparing the social welfare between the two different types of mortgage products. Because banks gain zero expected profit under either of the two mortgage products, the social welfare is calculated as the borrower’s expected payoff minus the expected liquidation cost of the collateral (1 − λ)p1.
Proposition 4.
There exists 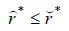 such that non-recourse mortgages yield (weakly) higher welfare than recourse mortgages
for all
such that non-recourse mortgages yield (weakly) higher welfare than recourse mortgages
for all 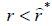 , but yields (weakly) lower welfare otherwise.
, but yields (weakly) lower welfare otherwise.
Proof.
Because LDP equilibrium arises from any r ≥ 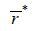 , both recourse mortgages and non-recourse mortgages yield the same amount of welfare.
Consider
, both recourse mortgages and non-recourse mortgages yield the same amount of welfare.
Consider 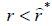 for which HDP equilibrium uniquely exists under a non-recourse mortgage. The net
borrower’s surplus from the non-recourse mortgage is UHDP − UR = UHDP − ULDP = (1 − π) y (λpl − r). Given that the borrower defaults on the mortgage debt in the state p1 + w1 = pl + wh with a non-recourse mortgage, shifting to a non-recourse mortgage adds an expected
cost of default (1 − π) y ( 1 − λ)pl to the welfare amount; thus, the net welfare of the non-recourse mortgage is (1 −
π) y (λpl − r) − (1 − π) y (1 − λ) pl = (1 − π) y ((2λ − 1) pl − r). Therefore, there exists
for which HDP equilibrium uniquely exists under a non-recourse mortgage. The net
borrower’s surplus from the non-recourse mortgage is UHDP − UR = UHDP − ULDP = (1 − π) y (λpl − r). Given that the borrower defaults on the mortgage debt in the state p1 + w1 = pl + wh with a non-recourse mortgage, shifting to a non-recourse mortgage adds an expected
cost of default (1 − π) y ( 1 − λ)pl to the welfare amount; thus, the net welfare of the non-recourse mortgage is (1 −
π) y (λpl − r) − (1 − π) y (1 − λ) pl = (1 − π) y ((2λ − 1) pl − r). Therefore, there exists 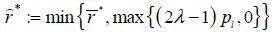 such that a non-recourse mortgage yields higher welfare than a recourse mortgage.
such that a non-recourse mortgage yields higher welfare than a recourse mortgage.
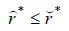 is immediate from (2λ − 1) < λ. Q.E.D.
is immediate from (2λ − 1) < λ. Q.E.D.
The default option granted to the borrower yields a potential welfare loss from the
costly liquidation process. Thus, a non-recourse mortgage can improve the total welfare
only if the borrower’s value of the default option is sufficiently high. This can
occur if and only if the opportunity cost of default - r ≥ 0 in our model – is sufficiently low (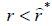 ). In contrast, such a welfare improvement effect no longer exists once the cost of
default is relatively high (
). In contrast, such a welfare improvement effect no longer exists once the cost of
default is relatively high (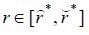 ). Therefore, as argued similarly in Proposition 3, it is important to investigate whether or not prospective users of non-recourse
mortgages want to buy houses either as an investment or as a residence.12
). Therefore, as argued similarly in Proposition 3, it is important to investigate whether or not prospective users of non-recourse
mortgages want to buy houses either as an investment or as a residence.12
V. Optimal Mortgage Design under Informational Asymmetry
Thus far, we have assumed that the borrower’s surplus from retaining homeownership is publicly known to the lender. In reality, however, households subjectively define the value of retaining their homeownership. Moreover, banks cannot precisely verify whether prospective borrowers want to buy housing properties for speculative purposes or for residential purposes. Hence, the main result in Section 4 may not have relevance.
To add reliability, we augment our model by introducing informational asymmetry to
the household’s surplus from homeownership r > 0. Specifically, we assume that nature draws 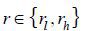 such tha 0 < rl < rh < ∞ with probability Pr ( r = rh) = q ∈ (0, 1) before the game begins. The borrower privately knows the true value of r . For convenience of exposition, we throughout refer to
such tha 0 < rl < rh < ∞ with probability Pr ( r = rh) = q ∈ (0, 1) before the game begins. The borrower privately knows the true value of r . For convenience of exposition, we throughout refer to 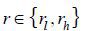 as the borrower’s “type.” To restrict our attention to the cases of interest, we
assume the following:
as the borrower’s “type.” To restrict our attention to the cases of interest, we
assume the following:
Assumption 3. 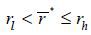
The main question is whether there exists a mechanism which addresses the adverse selection problem potentially faced by a type-rh borrower. As argued previously, the borrower with type rh is more willing to repay her mortgage debt than the other type. At a glance, one may conjecture that the type-rl borrower has an incentive to mimic type rh for more favorable borrowing terms. If a borrower of type rh is lumped together with those of type rl, her borrowing terms will be worsened to an extent that she may default in states she would not given complete information. The following proposition holds that the adverse selection problem of the mortgage market can be fully eliminated under a non-recourse mortgage only if rl is relatively high.
Proposition 5.
(i) If 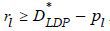 , there exists a separating equilibrium by which a borrower of type rl borrows with repayment term
, there exists a separating equilibrium by which a borrower of type rl borrows with repayment term 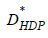 and a borrower of type rh borrows with repayment term
and a borrower of type rh borrows with repayment term 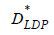 under a non-recourse mortgage.
under a non-recourse mortgage.
(ii) If 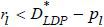 , there exists no separating equilibrium under a non-recourse mortgage.
, there exists no separating equilibrium under a non-recourse mortgage.
Proof.
To prove part (i), recall from the proof of Proposition 2 that the borrower will gain UHDP if she reports her type as rl and ULDP if she reports her type as rh. Recall also that UHDP − ULDP > 0 if r = rl and UHDP − ULDP < 0 if r = rh.
First, we show that it is optimal for each type of borrower to utilize the prescribed equilibrium strategies. Consider a borrower of type rl first. Because UHDP − ULDP > 0, type rl has no incentive to misreport her type as rh. Likewise, a borrower of type rh cannot gain a higher payoff from mimicking type rl as UHDP − ULDP < 0 if r = rh.
We now show that banks have no incentive to deviate from the prescribed equilibrium
offer strategies. Because both 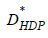 and
and 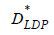 yield zero expected profit in equilibrium, banks offering either
yield zero expected profit in equilibrium, banks offering either 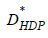 and
and 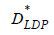 have no incentive to make the other offer. If a bank deviates and offers D' >
have no incentive to make the other offer. If a bank deviates and offers D' > 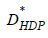 , then no borrower will buy the mortgage from this bank. Moreover, any offer
, then no borrower will buy the mortgage from this bank. Moreover, any offer 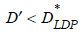 leads to a loss to banks regardless of whether such an offer attracts type rl, type rh, or both. Suppose a bank offers
leads to a loss to banks regardless of whether such an offer attracts type rl, type rh, or both. Suppose a bank offers 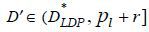 . If type rh buys the mortgage from this bank, her total payoff will be strictly less than ULDP. If type rl buys the mortgage from this bank, her payoff is then strictly less than ULDP. Because UHDP > ULDP for r = rl, type rl will not buy the mortgage from the deviating bank. Lastly, suppose a bank offers
D' > Pl + r. Proceeding similarly as in the previous argument, one can find that no type will
buy the mortgage under such repayment terms.
. If type rh buys the mortgage from this bank, her total payoff will be strictly less than ULDP. If type rl buys the mortgage from this bank, her payoff is then strictly less than ULDP. Because UHDP > ULDP for r = rl, type rl will not buy the mortgage from the deviating bank. Lastly, suppose a bank offers
D' > Pl + r. Proceeding similarly as in the previous argument, one can find that no type will
buy the mortgage under such repayment terms.
We next prove part (ii). Suppose there is a separating equilibrium under a non-recourse mortgage. A borrower of type rl can then gain a strictly large payoff by being untruthful regarding her type, i.e., reporting it as r = rh, and defaulting on her repayment in the state of p1 + w1 = pl + wh, a contradiction. Q.E.D.
Suppose rl is relatively high to an extent that she will not exercise her default option with
the low repayment term 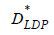 . For a type-rl borrower, the default option is valuable compared to the lower mortgage rate (
. For a type-rl borrower, the default option is valuable compared to the lower mortgage rate (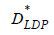 <
< 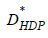 ) such that she can enjoy by lying about her type to the banks. In other words, the
repayment term
) such that she can enjoy by lying about her type to the banks. In other words, the
repayment term 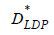 offered to type r = rh in equilibrium is not favorably low enough for the type-rl borrower to mimic the other type. In contrast, the type-rh borrower finds exercising the default option too costly due to the high value of
her homeownership surplus. Hence, type-rh prefers a contract with the lowest repayment term (D =
offered to type r = rh in equilibrium is not favorably low enough for the type-rl borrower to mimic the other type. In contrast, the type-rh borrower finds exercising the default option too costly due to the high value of
her homeownership surplus. Hence, type-rh prefers a contract with the lowest repayment term (D = 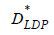 ), which is offered when the type-rh borrower truthfully reports her own type. On the other hand, such a separating equilibrium
cannot be supported if rl is too low; a borrower of type rl will realize high gains by misreporting her type for the favorable mortgage rate
), which is offered when the type-rh borrower truthfully reports her own type. On the other hand, such a separating equilibrium
cannot be supported if rl is too low; a borrower of type rl will realize high gains by misreporting her type for the favorable mortgage rate
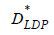 and exercising the default option in the state p1 + w1 = pl + wh. In order to ensure truth-telling to be a compatible incentive for type rl, a non-recourse mortgage with repayment term
and exercising the default option in the state p1 + w1 = pl + wh. In order to ensure truth-telling to be a compatible incentive for type rl, a non-recourse mortgage with repayment term 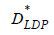 in the menu of mortgage contracts should be replaced by a recourse mortgage product
with the same repayment term.
in the menu of mortgage contracts should be replaced by a recourse mortgage product
with the same repayment term.
One interesting feature is that information rent is not given to any type of borrower in the separating equilibrium stated in Proposition 5. However, it remains an open question as to whether we have the same result when the mortgage market is not as competitive, as in our model. In fact, the bank’s increased market power is likely to decrease the borrower’s expected gains from using mortgage services in a non-linear fashion. Hence, how the level of information rent given to certain types of borrower changes with the degree of competition among banks in the mortgage market deserves a thorough analysis.
We can derive a policy implication from Proposition 5: setting a limit on the interest rate of non-recourse mortgage products may not improve a (non-speculative) borrower’s gains. When introducing non-recourse mortgage instruments into the market, policymakers are plausibly concerned that high mortgage rates due to the increased default risk may worsen households' debt problems. In order to protect households from hefty repayment duties, policymakers may regulate banks by ordering them not to charge high interest rates to borrowers using non-recourse mortgage products.13 However, such a measure may prevent households with high levels of residential demand from distinguishing themselves from speculative borrowers, exacerbating the adverse selection problem. For the same reason, prohibiting the sales of traditional recourse mortgage products may worsen the adverse selection problem in the mortgage market.
VI. Conclusion
This paper presents a simple reduced-form model to analyze how the provision of a default option to borrowers influences the level of default risk in the mortgage business. By defaulting on their debts under non-recourse mortgages, borrowers can prevent their non-collateralized income from being foreclosed upon. However, the default option is not always better for borrowers because lenders can raise mortgage rates.
We show that the equilibrium default probability under a non-recourse mortgage decreases as households enjoy a high surplus from retaining their purchased properties. We also find that a non-recourse mortgage can improve a borrower’s overall gains from mortgage financing (and their total welfare) if and only if the default option presents a sufficiently high value to borrowers. Lastly, we modify our model so that it contains the adverse selection problem in which the borrower’s surplus from homeownership is private information. We find that there exists a menu of non-recourse mortgage contracts that implements a separating equilibrium state without the payment of information rent to any type of borrower.
One avenue for future research is to analyze how each alternative type of the equilibria arises over the long run under aggregate levels of uncertainty. For instance, it is possible for certain changes in the probability distribution of future housing prices to lead to extraneous uncertainty via a self-fulfilling prophecy (Azariadis, 1981), which then causes a state of equilibrium with a high default probability to arise frequently over time even if borrowers' surplus amounts from homeownership are relatively high. An investigation of the mechanism of such self-fulfillment in a long-run model will have important policy implications regarding how to stabilize the mortgage market.
Another interesting topic would be to study whether households’ saving decisions are influenced by the types of mortgage contracts. Suppose that a household expects to finance their home purchase in the future via a traditional recourse mortgage contract. Because the default risk of a recourse mortgage is small, the household anticipates a low cost of buying the house and thus will not save a large portion of their current income for the home purchase. Furthermore, the household’s savings will be foreclosed upon in the event of a default, which implies the savings cannot serve as a buffer against negative income shocks. Therefore, one may conjecture that a household may save less under a recourse mortgage contract than it would otherwise. An analysis of the link between mortgage types and households’ consumption behaviors using a general equilibrium approach is an interesting area for future research.
Notes
The author thanks Sunjoo Hwang and other participants in the mid-term seminar on KDI policy research projects in July of 2017 for their comments and suggestions. The author deeply appreciates the anonymous reviewers for their invaluable feedback and for the suggestions which improved the paper. The views expressed in this paper are those of the author and do not necessarily represent those of the Korea Development Institute (KDI). All errors belong to the author.
See the following link for more details (in Korean): http://biz.chosun.com/site/data/html_dir/2017/01/13/2017011301418.html
This analytical result resonates with the empirical works by Bhutta et al. (2017) and Guiso et al. (2013). For instance, Bhutta et al. (2017) finds that borrowers are more reluctant to default on their mortgage repayment obligations than the level predicted by traditional models. They interpreted their finding as meaning that emotional and behavioral factors may influence borrowers’ repayment decisions. The surplus gained mortgage repayment in our model plays a role similar to such “non-rational” factors.
The heterogeneity of borrowers’ characteristics is similar to that in the setting of Campbell and Cocco (2015).
It may be more plausible to assume that banks offer a variety of contractual benefits to prospective borrowers. For instance, some banks may offer to relax the loan-to-value (LTV) constraint on the mortgage in order to attract borrowers who want to use high leverage for investing in real estate (Bester, 1985). However, it may not abstract from reality even if the mortgage rate is the only contractual term of the mortgage. In fact, any contractual terms exist in a replaceable relationship with the mortgage rate. Particularly, although there may be a state of equilibrium in which banks are allowed to offer various mortgage terms, one can also find another equilibrium state with a mortgage contract containing repayment terms only, in which the borrower gains the same utility as they would in any other state of equilibrium with a mortgage with various terms.
Because this paper focuses primarily on the strategic interaction between banks (lenders) and households (borrowers) at the institutional level, we abstract from potential issues pertaining to the allocation efficiency levels of collateralized properties at the market level.
This setup is standard in the finance literature, as in Diamond and Dybvig (1983) for the case of bank runs; and Brunnermeier and Pedersen (2008), Malherbe (2014), and Parlour and Plantin (2008) for cases of liquidity shortfalls in the secondary market. One may find that any alternative formulation of the default cost (such as a fixed cost imposed on the lending bank) does not change the main result.
More precisely, the household’s net income in t=1 is the sum of labor income w1 plus capital gains p1 − p0. However, it is more important in our analysis to focus on p1 + w1, which is the total amount of income payable to fulfil the mortgage. For convenience of exposition, we throughout the paper abuse the term “income,” which refers to the total amount of money which can be used to repay the mortgage.
The author is highly indebted to one of the anonymous referees, who pointed out an error in the proof of Proposition 2 in a previous version of this paper. The author also acknowledges that the same error was found in the baseline paper written by Rhee (forthcoming).
This result is consistent with Albanesi et al. (2017), which documents that borrowers’ residential levels of demand for housing properties are an important factor in determinations of default probabilities.
The result UR = ULDP does not change even if we relax the assumption of and allow wl = 0. Under a recourse mortgage, the borrower will lose her labor income wl in the worst state of p1 + w1 = pl + wl, but enjoys a lower repayment term 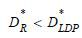 compared to that in a non-recourse mortgage. One can algebriacally find that this
tradeoff is precisely cancelled out.
compared to that in a non-recourse mortgage. One can algebriacally find that this
tradeoff is precisely cancelled out.
This result will not be substantially altered even if we assume that the borrower
is risk averse. To understand this easily, one can augment our model with an extra
reduced-form variable added to the borrower’s state-dependent payoff, which is zero
if the net income after repaying the mortgage is large and positive otherwise. In
this setup, the main result remains unchanged, although the value of the threshold
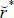 increases compared to that in the baseline model.
increases compared to that in the baseline model.
Similar to Proposition 3, the welfare comparison result in Proposition 4 will not be significantly altered even if we assume that the borrower is risk averse regarding her future consumption.
For instance, the Financial Supervision Committee (FSC) recently announced that the non-recourse type of Bogeumjari mortgage products as provided by the Korea Housing-Finance Corporation (HF) will charge interest rates identical to those of recourse mortgage products. For more details, see the new article (in Korean) posted at the following website: http://www.fnnews.com/news/201701151722011785
References
(1981). Self-fulfilling prophecies. Journal of Economic Theory, 25(3), 380-396, https://doi.org/10.1016/0022-0531(81)90038-7.
, , & (2017). Consumer ruthlessness and mortgage default during the 2007 to 2009 housing bust. The Journal of Finance, 72(6), 2433-2466, https://doi.org/10.1111/jofi.12523.
, & (2015). A model of mortgage default. The Journal of Finance, 70(4), 1495-1554, https://doi.org/10.1111/jofi.12252.
(2013). Evidence on the benefits of alternative mortgage products. The Journal of Finance, 68(4), 1663-1690, https://doi.org/10.1111/jofi.12049.
, & (1983). Bank Runs, deposit Insurance, and liquidity. Journal of Political Economy, 91(3), 401-419, https://doi.org/10.1086/261155.
, & (2011). Recourse and residential mortgage default: evidence from US states. The Review of Financial Studies, 24(9), 3139-3186, https://doi.org/10.1093/rfs/hhr055.
, , & (2013). The determinants of attitudes toward strategic default on mortgages. The Journal of Finance, 68(4), 1473-1515, https://doi.org/10.1111/jofi.12044.
, , & (2015). Mortgage defaults. Journal of Monetary Economics, 76, 173-190, https://doi.org/10.1016/j.jmoneco.2015.09.011.
(2015). Household’s optimal mortgage and unsecured loan default decision. Journal of Macroeconomics, 45, 222-244, https://doi.org/10.1016/j.jmacro.2015.05.002.
(2014). Self fulfilling liquidity dry ups. The Journal of Finance, 69(2), 947-970, https://doi.org/10.1111/jofi.12063.
, & (2008). Loan sales and relationship banking. The Journal of Finance, 63(3), 1291-1314, https://doi.org/10.1111/j.1540-6261.2008.01358.x.
, & (2010). Optimal mortgage design. The Review of Financial Studies, 23(8), 3098-3140, https://doi.org/10.1093/rfs/hhq031.
(1978). Default risk under alternative mortgage instruments. The Journal of Finance, 33(5), 1279-1296, https://doi.org/10.1111/j.1540-6261.1978.tb03420.x.