
The Effects of Institutions on the Labour Market Outcomes: Cross-country Analysis
Abstract
This paper re-examines the impacts an institutional arrangement may have on labour market outcomes such as the employment and unemployment rates. Based on the results from a generalized econometric model, the generosity of unemployment insurance benefits, organized labour and active labour market policy have effects on a labour market in line with previous findings. However, taxes on labour and the degree of employment protection are found to affect neither the employment rate nor the unemployment rate. Thus, some findings in this paper validate earlier findings, whereas others do not.
Keywords
Employment Rate, Unemployment Rate, Labor Market Institutions, Cross-country Analysis
JEL Code
C01, J08, J21, P51
I. Introduction
Since the 1980s, OECD countries have witnessed that common economic shocks yield different labour market outcomes for each country. Some fared well, while many others fared poorly. These cross-country differences appear to be persistent rather than temporary, having profound implications.1 When considering these observations, researchers have begun to pay more attention to the role institutions play in labour market outcomes.
The importance of institutions in a labour market has been well recognized. Labour market institutions such as employment protection legislation, unionization, taxes on labour earnings and work-related benefits differ from country to country, and by exploiting these variations, many studies have investigated the impacts the institutional factors may have on labour market performances. Researchers generally conclude that institutional obstacles (known as “labour market rigidities”) could lower flexibility and mobility in a labour market and hence result in poor performances and low growth.2
It is fair to say, however, that the relationship between the institutional variables and labour market outcomes is not as clear as one may think. The results of previous findings are mixed: some studies confirmed an effect of an institutional variable on labour market outcomes, while others failed to find convincing evidence of such a linkage. Broadly speaking, there are two primary reasons for this. First, needless to say, the limited data availability and related comparability issues in cross-country analyses are at least partially responsible for the mixed results. Different definitions of variables and unbalanced time periods to cover, and many other data-related problems are obstacles which arise when researchers attempt to come up with correct inferences. Over years, the OECD has made strenuous efforts to improve data quality levels for cross-country analyses. Ambiguous results may partly arise from an insufficient understanding of the mechanisms through which institutional variables work. In other words, the question “How are labour market institutions related to economic performance?” must be handled with an appropriate representation of an econometric model and methodologies, as the results crucially depend on these factors. This paper indicates the problems that conventional approaches may have and proposes more flexible and practical empirical strategies.
The adequacy of the econometric model and methodology in this analysis produces results in contrast to those found in earlier studies. In spite of the advantages of the standard panel estimation approach adopted in previous studies, that method can fail to capture complicated data-generating processes commonly found in analyses of macro-variables in panel structures. This paper generalizes econometric specifications as a close approximation of reality without adding excessive computational burdens.
The questions asked here are to what extent labour market institutions matter and in which directions a variable may affect labour market outcomes such as the employment and unemployment rates. Using a generalized econometric model, some of the estimation results validate what previous studies have found, whereas others do not.
The paper is organized as follows. The next section introduces the background of labour market performances for the selected OECD countries. Section 3 reviews the findings in previous studies about the implications of labour market institutions. The econometric model used and the methodology adopted here are introduced in Section 4. Section 5 explains the data and presents the results. Section 6 concludes this paper.
II. Labour Markets of the Selected OECD Countries
Labour market performances of OECD countries appear to undergo sizable changes over time and show substantial variations across countries. Figure 1 illustrates the selected OECD countries’ employment rates and unemployment rates between 1985~1993 and 2000~2008. As shown, employment rates have improved substantially over time in Spain and the Netherlands, while countries such as Germany, Denmark, France, Norway, the UK and the US show only slight improvements. Exceptions are Finland and Sweden, where employment rates have deteriorated over time. The levels of employment differ significantly among the countries. In the period of 2000 to 2008, the employment rates range from approximately 56% (Italy) to 76% (Norway), showing a 20%p gap.
The unemployment rate also shows sizable cross-country variations ranging from 3.7% (Norway) to 10.6% (Spain) for 2000-2008. These figures show that the unemployment rates for 2000-2008 are lower than those for 1985-1993. The unemployment rates declined sharply in Spain and the Netherlands, as these countries marked significant improvements in their employment rates.
Various factors have been posited with regard to the cross-country variations and secular trends in the labour market outcomes. Cyclical shocks, not only countryspecific but also common to countries, can yield different employment rates and unemployment rates, as they affect the countries’ economies in distinct ways. In addition, institutional factors such as the environment, practices and legal framework can cause a country’s labour market performance to different from those of others. Many studies have investigated the effects of labour market institutions while focusing on several institution-related variables, such as taxes on labour (tax wedge), the level of unemployment insurance benefits (replacement rate), organized labour (union density), the degree of employment protection, and measures which become labour market policies. There are extensive works on how and why these variables matter in labour market outcomes, which will be discussed in the next section.
III. Literature Review
Voluminous studies have focused on the roles of labour market institutions in determining labour market performance. Some of them directly analyzed this relationship empirically and others investigated related issues indirectly. Most papers focused on the impact taxes on labour, unemployment benefits, employment protection, and organized labour (unions) may have on the employment and unemployment rates. Some studies also include policy variables such as active labour market policies (ALMP). What is known thus far is that in general, policy variables and the institutional mechanisms do matter with regard to labour market performances. From extensive works on this issue, the relationship between a certain institutional variable and labour market performance has been found to be clear and unambiguous, whereas others links remain inconclusive.
The following sections summarize the effects of various institutions on labour market outcomes as found in earlier empirical studies.
• Taxes on labour (or the tax wedge)
Theoretically, it can be shown that the tax wedge (determined by taxes on payroll, consumption and income) affect labour supply and demand levels and hence likely affect the labour market. Whether its main impacts are on employment or on wages depends on the nature of the labour market.3 Empirical results are mixed. Some studies confirm a significant and sizable effect on labour market performances (Pichelmann and Wagner, 1986; Nickell, 1997; Nickell and Layard, 1999; Elmeskov et al., 1998; Belot and Van Ours, 2000) while others report ambiguous results (Scarpetta, 1996; Daveri and Tabellini, 2000; Nicoletti and Scarpetta, 2001)
• Unemployment insurance (or the benefit replacement rate)
From a labour supply perspective, a high replacement rate can lower an individual’s search intensity, raising unemployment. On the other hand, generous unemployment insurance may make the labour market more attractive, increasing the participation rate. These two opposite effects of the benefit replacement rate can make the impact on the labour market ambiguous. Many empirical studies support the contention that generous benefits are associated with a high unemployment rate. Meanwhile, studies focusing on the employment rate have not found negative effects with statistically significant levels.
• Union
The relationship between labour unions and overall labour market outcomes is not well understood. A union as a rent seeker may have negative influence on labour market outcomes by restricting employment. On the other hand, a union as an insurance provider could minimize unemployment by enhancing employment possibilities. Thus, what a union does to labour market outcomes requires an empirical question. Thus far, empirical results do not appear to provide a clear answer. Some studies find a negative effect on the labour market, but it is believed that the relationship is much more complicated (Scarpetta, 1996; Nickell and Layard, 1999; Nicoletti and Scarpetta, 2001). As posited in previous studies, the factors that matter are the degree of employer-employee coordination and the coverage of collective bargaining (Clamfors and Driffill, 1988; Summers et al., 1993; Scarpetta, 1996; Elmeskov et al., 1998). Unfortunately, the measures for these variables are questionable in terms of their quality and reliability (Daveri and Tabellini, 2000).
• Employment protection
Employment protection is perceived to be a key element causing labour market rigidity (Lazear, 1990). Employment-protection-induced rigidity may proceed in two directions (Bertola, 1990; Hopenhayn and Rogerson, 1993; Nickell, 1997): it can reduce inflows into employment in expansionary phases on the hand, whereas it can reduce outflows from employment during economic contractions on the other. Some are skeptical of its effect because the primary effect may not be on the level of labour market outcomes (such as the employment or unemployment rates) but rather on the compositions (such as longer unemployment durations particularly for groups at the margins in a labour market for those who are selfemployed) (Blanchard and Wolfers, 2000)4 The findings of most empirical studies indicate a negative effect, implying that the stricter the regulations are, the worse the labour market outcomes become (Lazear, 1990; Scarpetta, 1996; Elmeskov et al., 1998; OECD, 1999), though a few studies report negligible impacts (Bertola, 1990; Grubb and Wells, 1993; Garibaldi et al., 1998; Nickell, 1997). Researchers seem to agree that employment protection affects groups (women, youth, elderly and etc.) differently in the labour force and that this complicated mechanism is one of the reasons why the overall effect of employment protection remains unclear.
• Active labour market policy (ALMP)
Given all of the concern over the deadweight/substitution/displacement effect, ALMP is believed to produce better labour market outcomes by facilitating jobmatching processes and accumulating human capital, for instance. Several empirical results confirm its effects on the unemployment rate (Elmeskov et al., 1998; Nickell and Layard, 1999), though others do not (Scarpetta, 1996; Belot and Van Ours, 2000). The effects of ALMP on the employment rate are not verified (Nickell, 1997; Nickell and Layard, 1999). Overall, the effects of ALMP on labour market outcomes are mixed and only marginally significant if at all.5
Table 1 reports the empirical results from the selected studies.
TABLE 1
LABOUR MARKET INSTITUTIONS AND OUTCOMES
Note: 1) e and u are the employment rate and unemployment rate, respectively. 2) Numbers in parentheses are: † for standard errors and * for the t-ratio.
Source: 1) Employment rate: Nickell (1997) column (1) of Table 7 on p.65; OECD (1999) column (1) of Table 2.10 on p.80; Nickell and Layard (1999) column (1) of Table 16 on p.3054; Nicoletti & Scarpetta (2001) column (4) of Table 4 on p.29. 2) Unemployment rate: Scarpetta (1996) column (3) of Table 1 on p.58; Elmeskov et al. (1998) column (5) of Table 2 on p.216; Nickell and Layard (1999) column (1) Table 15 on p.3053; Daveri and Tabellini (2000) column (7) of Table 9 on p.75; Belot and van Ours (2000), column (1) of Table 6 on p.30.
IV. Econometric Model
This section starts with a standard panel econometric specification used in previous studies and then defines several problems associated with the model. To address these issues, an extended econometric model is proposed. The generalized model, however, poses some challenges with regard to conventional estimation techniques. A few existing studies of econometric techniques provide solutions for an estimation strategy partially, but not completely. Limitations on datasets such as a short time dimension and incomplete and unbalanced features further restrict the degree of choice of a feasible method.
Facing these difficulties, this paper suggests a flexible and practical estimation strategy for a dynamic panel model with time-varying individual effect and serially correlated error terms. This method is particularly attractive because it can be applied to an incomplete panel dataset. Bayesian estimation techniques adopted in this study are well developed in panel data models and have been applied to a wide variety of models, such as continuous, binary, censored, count, and multinomial response models.6
If there is a method by which to determine the likelihood of a model, the distributions of parameters, otherwise analytically intractable, can be characterized by numerical procedures such as MCMC methods. In general, the likelihood function of a model that includes latent variables with Gaussian errors can be obtained via a Kalman filter once we have a linear state space representation. In the following section pertaining to the estimation strategy, we show a linear state space transformation of our model and furthermore how a Kalman filter is modified to evaluate the likelihood of the model with an incomplete panel dataset. Consequently, with the specification of prior distributions which are introduced only to prevent autoregressive parameters from implying non-stationary processes, the Metropolis Hasting MCMC algorithm enables us directly to characterize the posterior distributions of the parameters of interest.
The estimation strategy proposed in this paper has several advantages which should be noted from an inference point of view. First, this methodology produces not only point-wise values of estimated coefficients but also their posterior distributions. This rich information enables a researcher to infer more accurate relationships between labour market institutions and employment/unemployment rates. Second, Bayesian estimation naturally allows us to perform model comparisons with Bayes factor or ratios of marginal likelihood. If there is an alternative model which can be used in a comparison with a benchmark model, the Bayes factor can tell which model is a better fit in light of available data.
A. Models
In order to assess the effects of institutional factors on labour market performances (e.g., the employment rate), many studies posit a standard panel econometric model, such as that shown below.
Here, yit is the employment rate for country i at time t , xit is a vector of k regressors (including a constant and time-dummies if necessary), βx is a parameter vector to be estimated, ξi is denote the time-invariant country-specific heterogeneity, and νit is a time-varying error term (white noise). When estimating (1), ξi is taken into account by applying generalized least square (random effect) or differencing methods (fixed effect) on first-differenced, mean-differenced, or long-differenced data.
Despite a couple of advantages, such as simplicity and tractability, fitting (1) may not be appropriate for the underlying data-generation process and may be misleading for the following reasons. First, as in most time-series data analyses, an aggregated macro-dependent variable (employment rate) appears to depend substantially on its past value. That is, yit is not likely to be independent of it yit-1(assuming that causality runs from the past to the present and not vice versa).
Second, (1) fails to capture the complicated effects of a contemporaneous shock. A
possible means of controlling for a contemporaneous shock is to include a time-dummy
variable (Dt) in (1) such as 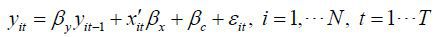 . This specification, however, assumes an unnecessarily strong neutrality of a contemporaneous
shock in a sense that all countries are affected by the shock in the same direction
to the same degree. Obviously, an economic shock commonly affecting many countries
yields sizable cross-country differences in the responses of the countries.
. This specification, however, assumes an unnecessarily strong neutrality of a contemporaneous
shock in a sense that all countries are affected by the shock in the same direction
to the same degree. Obviously, an economic shock commonly affecting many countries
yields sizable cross-country differences in the responses of the countries.
Third, the assumption of the error term (νit) in (1) is unnecessarily strict. A time-dependent error term, particularly in a macro-dependent variable, is likely to be serially correlated due to inertia in a dependent variable due to variables (other than ξi) being excluded from the right-hand side of (1).
To address these problems, this study considers an extended version of (1) with a dynamic error-component, as follows:
Unlike (1), (2) includes a lagged dependent variable as a regressor in order to capture persistence in the employment rate. The error component, εit, in (1) is modified in two ways. First, a country-specific effect, ξi, is multiplied by a time-varying common factor (i.e., Ψtξi) in order to capture how a common shock may have different responses across countries. Second, the white noise error term νit in (1) is allowed to have a serial correlation in order to account for the possibility of employment rate inertia arising from variables not included in (2).
An auto-regressor (yit-1), time-varying common factor (Ψtξi), and serially correlated error term (νit) when arising together poses serious challenges when attempting to estimate the parameters in (2). Conventional panel estimation techniques are undesirable because they cannot remove the endogeneity between Δyit-1(=yit-1-yit-2) and Δνit(=νit-νit-1). An attempt to use a high-order lagged response variable as an instrument (Arellano and Bond, 1991) also fails because the serially correlated νit is related to all past response variables. Furthermore, a simple differencing of (2) cannot control for country-specific heterogeneity because ξi multiplied by Ψt is no longer time-invariant.
Several methods which filter the unobserved individual heterogeneity component in linear models are readily available in the literature.7 However, these methods are only valid when the time-varying idiosyncratic error terms are not serially correlated. Although a differencing method with some extension can eliminate the time-varying individual effects and serial correlations of the error terms, using such a method leads to an equation in which the coefficients of the observable regressors are nonlinear functions of the original parameters. A standard linear regression will not be applicable in this situation, and the inference on the original parameters cannot be directly characterized. Moreover, the differenced equation includes high orders of lagged variables; thus, instrumental variables of higher orders of the lagged variable, reducing the size of the time observations of the dataset, are necessary to handle the endogeneity problem. This is undesirable, especially when the data is scant in the time dimension, a situation prevalent with panel datasets.
B. Estimation Methodology
We adopt a Bayesian approach to maximize the posterior distribution of parameters in the model. For the estimation, the Random Walk Metropolis Hastings MCMC method is used for the numerical procedure to characterize the posterior distribution. Because the posterior distribution is composed of the prior specified by the researcher’s belief about the parameters and of the likelihood - which needs to be numerically evaluated – the method used to evaluate the likelihood of the model is crucial. As the model includes complicated dynamics due to the autoregressive processes of latent variables, such as common factors and error terms, the model is transformed into a state space representation which becomes applicable for evaluating the likelihood using a Kalman filter. In addition, there is a need to modify the standard Kalman filter to accommodate an incomplete panel dataset. From a time-series perspective, an incomplete panel dataset can be considered as a dataset with partially missing observations for each period. The Kalman gain, which efficiently estimates the state of the following period using current observations, can be appropriately adjusted when certain observations of the current period are not available. The following subsections will illustrate the state space representation, the augmented Kalman filter to accommodate the incomplete panel dataset, and the Metropolis Hastings algorithm.
1. Kalman Filter with an Incomplete Panel Dataset
In order to apply the Kalman filter, (2) must be expressed by a linear state space representation. This representation is straightforward, as (2) is linear with Gaussian errors. In general, the linear state space form is expressed as follows:
H denotes the coefficient matrix in the observation equation, as H ≡ [Ξ IN] where Ξ = [ξ1, ⋯, ξN]′ and IN is the identity matrix with a dimension of N. The state variable, zt, is a vector of unobserved latent variables such that 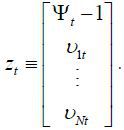 .
.
It is important to note that the long-run mean of the state vector is conveniently
zero. It follows immediately that the autoregressive coefficient matrix, F, is 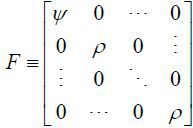 and the error term εt in the state equation is
and the error term εt in the state equation is 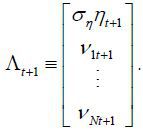 .
.
Consequently, we can also demean the left-hand side of the observation equation to match the zero mean with the right-hand side by defining Yt ≡ yt-yt-1βy-xtβx-1Nβc-Ξ, where yt ≡ [y1t, ⋯, yNt]′, xt ≡ [x1t, ⋯, xNt]′ and 1N is a column vector of ones.
When Yt is fully observed, the standard Kalman Filter allows to estimate zt by minimizing the predicted error variance-covariance matrix of zt given the history of the observation until t. We define the covariance matrix of zt as ∑t; then, the standard Kalman filter procedures are as follows:
1. Given zt|t-1 and ∑t|t-1, observe Yt
2. Yt|t-1 =HZt|t-1
3. Kt = ∑t|t-1H′(H∑t|t-1H′)-1
4. ∑t|t = ∑t|t-1 - KtH∑t|t-1
5. zt|t = zt|t-1 + Kt(Yt - HZt|t-1)
6. ∑t+1|t = F∑t|tF′ + Q
7. Zt+1|t = FZt|t.
For an incomplete panel dataset, step 5 in the procedure above is not implementable
because Yt is not fully observed in some periods. As Harvey (1991) has proposed, we can update the Kalman gain using only available information. Without
a loss of generality, we can for instance observe 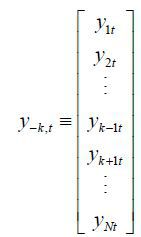 but not observe ykt. We can use the corresponding partitions of H and Kt accordingly with the available observations of K-k,t = [K1t, K2t ⋯ Kk-1t, Kk+1t, ⋯ KNt]
but not observe ykt. We can use the corresponding partitions of H and Kt accordingly with the available observations of K-k,t = [K1t, K2t ⋯ Kk-1t, Kk+1t, ⋯ KNt] 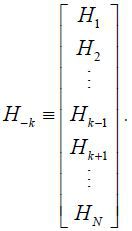 .
.
Step 5 will then be updated, as zt|t = zt|t-1 + K-k,t(Y-k,t-H-kzt|t-1).
In general, if yt randomly has missing observations other than the kth element, we need to eliminate the corresponding rows of Kt and H.
2. Metropolis Hasting MCMC Algorithm
The Bayesian approach to estimate the model is to randomly draw a set of parameters in which the posterior-density-maximizing parameters are drawn with higher probabilities. We define the set of parameters and the dataset as follows:
θ ≡ (βc, βy, βx, Ψ, Ξ, ρ, ση)
YT ≡ {y1, ⋯, yT}
The posterior density function is defined as shown below.
p(θ|YT) ≡ π(θ)l(θ|YT)
Given numerically drawn values of θ, the above posterior distribution can be evaluated using the modified Kalman filter. Subsequently, the Random Walk Metropolis Hastings algorithm can be implemented as follows:
1. Initialize θ(0) and evaluate p(θ(0)|YT)
2. Draw θ* ~ N(θ(k), 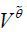 )
)
3. Evaluate p*(θ*|YT)
4. Accept or reject based on posterior odds 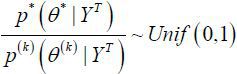
5. If accept, record θ(k+1) = θ* else θ(k+1) = θk
6. Go back to step 2
Step 2 is to draw θ* based on a normal distribution around the previously accepted draw θ(k) with variance 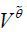 . In this random-walk sampling scheme, the practical convention for the choice of
. In this random-walk sampling scheme, the practical convention for the choice of
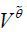 is the inverse of the Hessian of the likelihood function evaluated in the posterior
mode; i.e., l(
is the inverse of the Hessian of the likelihood function evaluated in the posterior
mode; i.e., l(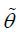 |YT) where
|YT) where 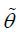 is the posterior mode. However, the posterior mode,
is the posterior mode. However, the posterior mode, 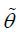 , clearly cannot be found directly and thus can be continuously updated with many
trials and errors involving different values of
, clearly cannot be found directly and thus can be continuously updated with many
trials and errors involving different values of 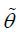 . An alternative is to use a simulated annealing method to search the posterior mode
and initiate the MCMC procedure given this posterior mode.8 Whether the choice of
. An alternative is to use a simulated annealing method to search the posterior mode
and initiate the MCMC procedure given this posterior mode.8 Whether the choice of 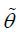 is valid or not can often be confirmed by the mixing properties, the convergence
statistics of the sequence of parameter draws and the acceptance rate.
is valid or not can often be confirmed by the mixing properties, the convergence
statistics of the sequence of parameter draws and the acceptance rate.
V. Data and Estimation Results
A. Data and Variables
The variables and dataset used in this study come from various sources. The employment rate, the ratio of those in employment to the working age population for those aged 15~64 years old, is obtained from OECD (2011). Data on the net replacement rate of unemployment insurance and on labour taxes are available from Vliet and Caminada (2012).9
The replacement rate (%) is defined as the ratio of net benefits to net earnings. Taxes on labour denote the effective tax rate (%) based on the actual tax wedge.10 Both variables are calculated at the average wage level for an average production worker. OECD (2010c) reports the union density as the ratio of the number of trade union members to all paid employees. This variable differs from the gross union density, which includes those who are unemployed, self-employed and unpaid family workers as a denominator.
Based on several indicators, OECD (2010a) reports a cross-country comparable measure for employment protection, which is the unweighted average of subindicators for regular and temporary employment. A government’s commitment to the labour market is proxied by its expenditures on active measures per unemployed person relative to output per capita (Scarpetta, 1996). Total expenditures on active labour market programs (category 10-70) are obtained from OECD (2010b). Finally, an output gap is included to control for cyclicality. It is calculated by A/T-1, where A is the actual GDP and T is the Hodrick-Prescott filtered GDP. Information on the real GDP comes from the Penn World Table (PWT version 7.1).
The dataset is an unbalanced panel of OECD countries from 1985 to 2009. The total number of observations is 492 from 28 countries. Most countries have approximately 20 observations on average, sizable and sufficient to facilitate a panel data analysis. Table 2 summarizes the dataset used in this study.
TABLE 2
SUMMARY STATISTICS
Note: There are 492 observations.
Sources: OECD (2010a), OECD (2010b), OECD (2010c), OECD (2011), PWT 7.1, and Vliet and Caminada (2012).
It is important to explore possible relationships between each institutional variable and the employment and unemployment rates graphically. Figure 2 and Figure 3 plot the employment rate and unemployment rate (on the vertical axis) against various institutional variables (on the horizontal axis).11 The partial correlations shown in the figures are, in general, consistent with the findings of previous studies: a tax on labour is negatively (positively) related to the employment (unemployment) rate, suggesting the possibility that a higher tax may be associated with a lower (higher) employment (unemployment) rate. Similarly, the replacement rate of unemployment insurance benefits and the union density appear to have a negative (positive) correlation with the employment (unemployment) rate, hinting that countries with generous unemployment benefits or more union members tend to have lower (higher) employment (unemployment) rates. Employment protection, on the other hand, is found to be weakly related to the employment (unemployment) rate. The direction of measures for active labour market policies is not apparent because a positive correlation appears to disappear once outliers (Netherlands and Sweden) are excluded.
Although the above figures suggest that a certain institutional variable are candidates to explain cross-country variations in labour market outcomes, the points in most figures are heavily scattered around the variables’ means, making it difficult to consolidate the relationships between labour market outcomes and institutional variables visually. Hence, precise inferences on the effect of institutional variables on labour market outcomes require an econometric analysis, as discussed in section 4.
B. Results
The estimation results with the choice of prior densities are presented in Table 3 (employment rate) and Table 4 (unemployment rate) and their corresponding posterior distributions are given in Figures 4 and 5.14 The prior distributions for the persistent parameters of Ψ, ρ, and βy are set to prevent the system from being non-stationary. While the prior distributions for ρ, and βy are neutral, that for Ψ is set to imply high persistence. Although the model allows for a time-varying common factor, we wanted to have common factor bounded within a small range.
Before discussing the institutional variables of our interest, the data confirms the GDP gap to be an important determinant of labour market outcomes, having a sizable positive effect on the employment rate and a negative effect on the unemployment rate. Therefore, it is fair to say that labour market outcomes are to large extent affected by the cyclicality of the economy.
When compared to earlier findings, special attention should be given when interpreting the results. First, the econometric model adopted in this paper is more generalized and elaborate compared to those in previous studies. Second and more importantly, the estimated coefficients reported in this paper are more concerned with long-term effects rather than those based on the short-term year-to-year variations in previous studies.15
Bearing this in mind, some of the results in this paper are in line with the findings of previous studies, whereas others are not. The results consistent with the previous studies are as follows:
• The effect of the replacement rate (βx2) on the unemployment rate
In the unemployment rate equation, the estimated coefficient is positive (with its mode equal to 0.024). The positive support its posterior distribution locates hints that the replacement rate is directly related to the unemployment rate (Scarpetta, 1996; Elmeskov et al., 1998; Nickell & Layard, 1999; Belot & van Ours, 2000).
• The effect of the union (βx4) on the employment rate and unemployment rate
The estimated coefficient of a union as measured by its density has a negative mode (-0.022) in the employment rate equation. With 90% of the posterior distribution having a negative value of βx4, and it is fair to say that a high union density may lower the employment rate (Nicoletti & Scarpetta, 2001).
• Although the estimated coefficient has a mode with a slightly positive value (0.005) in the unemployment rate equation, the effect of a union on the unemployment rate is inconclusive, as shown by its posterior distribution. The support ranges from a negative to a positive value, implying that the estimated coefficient could be either case with considerable probabilities. In fact, the estimated coefficient of union density was found to be positive (Scarpetta, 1996; Nickell & Layard, 1998), negative (Elmeskov et al., 1998) or even insignificant (Belot & van Ours, 2000).
• The effect of employment protection (βx5) on the unemployment rate
For the unemployment rate, the estimated result shows that employment protection may have either positive or negative effects, as shown by its less informative posterior distribution. To some extent, this finding is consistent with mixed results found in previous studies.
• The effect of ALMP (βx6) on the unemployment rate
In the unemployment equation, the mode of the ALMP coefficient appears to be -0.019, and its posterior distribution indicates that βx5 is very likely to have a negative value. From this result, it is safe to say that ALMP may lower the unemployment rate (Elmeskov et al., 1998; Nickell & Layard, 1998).
On the other hand, the following results are different from what the previous studies reported.
• The effect of the replacement rate (βx2) on the employment rate
Unlike previous empirical studies, the estimated coefficient of the replacement rate in the employment rate equation has a mode of -0.024 with 90% of its posterior distribution lying well below zero. Hence, the data suggest that a higher replacement rate is associated with a lower employment rate.
• The effect of labour taxes (βx3) on the employment and unemployment rates
The estimation result could not convincingly support the negative (positive) effects of taxes on the employment (unemployment) rate found in previous research. Because a posterior distribution is less informative with regard to the value of this parameter, it is difficult to judge whether the estimated coefficient of taxes has a positive or negative value.
• The effect of employment protection (βx5) on the employment rate
Unlike the negative effect reported in previous studies, the impact EPL may have on the employment rate is found to be inconclusive due to the less informative posterior distributions. Although the estimated coefficient has a mode of -0.331, its confidence cannot be maintained by its posterior distribution.
• The effect of ALMP (βx6) on the employment rate
In contrast to the previous result showing no direct relationship between ALMP and the employment rate, the measure for ALMP in the employment equation in this study has an estimated coefficient of a positive mode (0.022) with the support of its posterior distribution entirely being in a positive range. This result implies that ALMP is very likely to raise the employment rate.
In summary, there are several points to note. First, the effects of employment protection on labour market outcomes are not confirmed. This does not mean that employment protection is relevant to labour market performances. In fact, as indicated in many studies, employment protection has a profound impact on inflows/outflows in the labour market as well as on the composition of labour market participants (Blanchard and Wolfers, 2000). This result can be interpreted by considering that the primary effect of EPL in the long run may rest not on the level of labour market outcomes but on other aspects of the labour market.
Second, surprisingly, the commonly recognized effect of taxes on labour does not appear either in the employment rate or unemployment rate. A possible explanation is that the primary effect of taxes on labour may be on the level of wages and not on the level of employment or unemployment. This is particularly true in the long run, when a labour market fully adjusts tax incidences.
Finally, an active labour market policy appears to reduce the level of unemployment, while other many institutional variables such as taxes on labour, the union density, and the degree of employment protection do not. Card et al.(2010) assessed the effectiveness of various active labour market programs in a meta-analysis of 199 programs of the OECD countries and concluded that job search assistance and training programs are effective in the long and medium terms. Hence, this result may reflect the large share of employment services and training spending in OECD active labour market policies.16
VI. Conclusion
This comparative study re-examines the role institutional arrangements play in labour market outcomes using panel data from selected OECD member countries. While many studies recognize countries’ institutional differences as an important factor explaining variations in employment and unemployment, the empirical results are far less satisfactory. This is partly due to data limitations and the econometric methods applied in the analysis.
The contribution of this paper is twofold. First, owing to the effort of the OECD in collecting data, this study can utilize highly qualified information consistently defined over a long period. This enables us to exploit the advantages and benefits panel data can provide. Secondly and more importantly, the econometric model adopted in this paper is modified in order to reflect the dynamic features of labour market reality while fully incorporating the heterogeneity of each country. Moreover, this complicated model can be estimated through the relatively simple strategies proposed in the paper.
Some of results in the paper are generally consistent with what previous studies have found while others are somewhat different. For instance, the level of UI replacement appears negatively to affect labour market outcomes such that generosity in this regard raises the unemployment rate. The organized labour and active labour market measures have effects in line with those in previous findings.
Other variables known to be important in determining labour market outcomes are found to have weak long-run relationships with the levels of overall employment and unemployment. Notably, taxes on labour have neither an effect on the employment rate nor on the unemployment rate. In addition, the estimation result hints that the primary effect of employment protection may not be on the level of overall employment or unemployment and may rather be on other labour market aspects, such as in-and-out flows and/or the composition of labour market participants.
Although this study investigates the relationship between institutional environments and labour market performance outcomes, it nonetheless leaves many unanswered questions. Above all, institutional variables, by nature, are very difficult to measure or summarized using a single index or number. The proxies for institutional variables in most empirical studies are typically error-ridden, and the results from troubled variables are prone to be biased. More seriously, the institutional arrangements are not purely exogenous but are endogenous. Again, the endogeneity make it difficult for a researcher to reach a correct inference from the results. These issues must be explored further in the future.
Notes
Daveri and Tabellini (2000) reported a sharp contrast in the long-term trend of the unemployment rates between European countries and the US.
One may expect that tax effects would be mostly on wages rather than on employment if the labour market is flexible enough to adjust fully for them. Blanchard and Wolfers (2000) hold that “their [tax-wedge] incidence may be on the wage, not on employment.” (P. C13)
Bertola (1990) shows theoretically and empirically that employment protection (the provision of job security) and labour market performances do not have a strong relationship. He argued that a high level of employment protection induces alternative types of jobs (such as self-employment), to which it cannot apply.
Two reasons can be mentioned when explaining the mixed results. First, ALMP consists of various policy measures which vary widely across countries, and an aggregated measure of ALMP fails to capture this variation. Second, more technically, an ALMP measure is endogenously determined with labour market outcomes such as unemployment. This may cause statistical inferences to be difficult and imprecise.
For example, Ahn et al. (2001) suggest quasi-differencing when the unobserved heterogeneity can vary across time periods, and Nauges and Thomas (2003) further extend the filtering method by double-differencing when the individual effects are both time-varying and time-invariant effects.
For data sources, see http://www.law.leidenuniv.nl/org/fisceco/economie/hervormingsz/datasetreplacementrates.html
The tax wedge denotes the labour costs that an employer should bear per worker minus the amount that the employee could take home. Thus, social insurance contributions and other cash benefits are included in the calculation of the tax wedge.
The estimation results without a serial correlation (i.e., ρ = 0 in (2)) are in the Appendix. In addition, the estimated results from a random-effect model based on (1) are presented in the Appendix.
References
, , & (2001). GMM estimation of linear panel data models with time-varying individual effects. Journal of Econometrics, 101, 219-255, https://doi.org/10.1016/S0304-4076(00)00083-X.
(2010). How to maximize the likelihood function for a DSGE model. Computational Economics, 35, 127-154, http://dx.doi.org/10.1007/s10614-009-9182-6, 0927-7099, https://doi.org/10.1007/s10614-009-9182-6.
(1990). Job security, employment and wages. European Economic Review, 34, 851-886, https://doi.org/10.1016/0014-2921(90)90066-8.
, , & . (2010). Active Labour Market Policy Evaluations: A Meta-Analysis. The Economic Journal, 120, F452-F477, https://doi.org/10.1111/j.1468-0297.2010.02387.x.
, & . (1993). Job Turnover and Policy Evaluation: A General Equilibrium Analysis. Journal of Political Economy, 101(5), 915-938, https://doi.org/10.1086/261909.
, & (1986). Labour surplus as a signal for real wage adjustment: Austria 1968-1984. Economica, 53, S75-S87, https://doi.org/10.2307/2554375.
, , & . (1993). Taxation and the Structure of Labor Market: The Case of Corporatism. The Quarterly Journal of Economics, 108(2), 385-411, https://doi.org/10.2307/2118336.
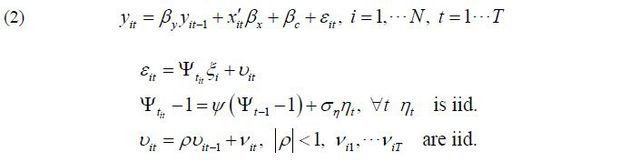
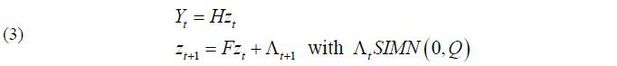
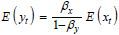 long-run effect.
long-run effect.