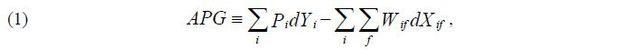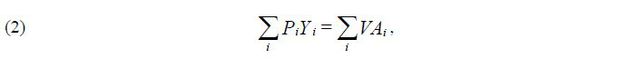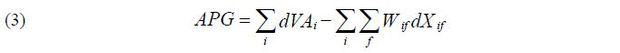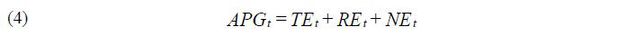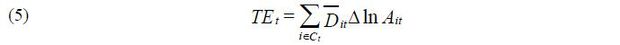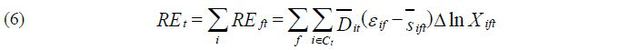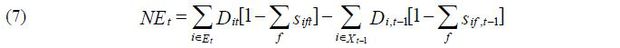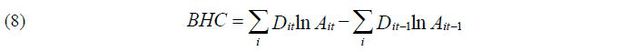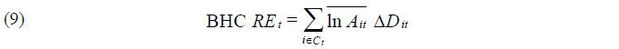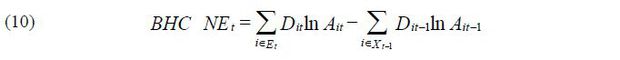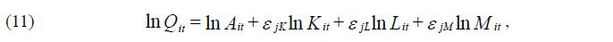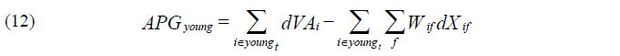Aggregate Productivity Growth in Korean Manufacturing: The Role of Young Plants
Abstract
I measure aggregate productivity growth in manufacturing between 1995 and 2013 as defined by Petrin and Levinsohn (2012). I decompose aggregate productivity growth into technical efficiency improvements, resource reallocations, and net entry effects. I find that aggregate productivity growth slows down after 2004 and that the rapid drop in technical efficiency growth contributed most to the decline. In this paper, I focus on the role of young plants with regard to productivity growth of Korean manufacturing. I show that young plants account for nearly half of APG (48%), while their value-added share is 14 percent on average between 1995 and 2013. I find that productivity growth at young plants has been declining for the last ten years. The lower growth of continuing young plants contributes to this trend. These results stress the important role of young plants in aggregate productivity growth and imply that understanding the dynamics of young plants is necessary to form effective start-up policies.
Keywords
Aggregate productivity growth, Productivity, Reallocation, Young plants
JEL Code
L6, L26, O47
I. Introduction
Manufacturing firms in Korea are exposed to competition with developed countries, including Germany, Japan, and the United States, in innovative products and services. They are also competing with Chinese firms in both domestic and foreign markets at a time when China is experiencing rapid growth in Korea’s flagship industries. This paper studies aggregate productivity growth in Korean manufacturing over the past two decades and investigates the sources of productivity growth.
Aggregate productivity can increase when plants increase their technical efficiency by developing or adopting new technologies, implementing process innovations, or improving their management system. However, without an increase in technical efficiency at plants, aggregate productivity can increase when resources are reallocated to a business with a higher market value. On the other hand, this also means that aggregate productivity can decrease when allocative efficiency decreases. Whether the decline in aggregate productivity is attributable to the stagnation of technical efficiency growth or to the decline in allocative efficiency is important when considering policies to maintain competitiveness. In this paper, I study the role of plant-level technical efficiency improvements, resource reallocations, and the net entry of plants in aggregate productivity growth.
I use plant-level data from the annual Mining and Manufacturing Survey provided by Statistics Korea to measure aggregate productivity growth in manufacturing between 1995 and 2013. I adopt the description of Petrin and Levinsohn (2012) (PL) of aggregate productivity growth (APG), where APG is defined as the change in aggregate final demand net of the change in expenditures on labor and capital. First, I need to estimate plant-level technical efficiency in order to estimate the contributions of plant-level technical efficiency improvements, resource reallocations, and the net entry of plants to APG. I apply the estimation method of Wooldridge (2009), which is a modified version of that by Levinsohn and Petrin (2003), to estimate the elasticity parameters of inputs in the production function. The elasticity parameters are estimated for every 82 three-digit industry.
The measured APG of the manufacturing industry is 5.7 percent on average between 1995 and 2013. During this period, technical efficiency growth is 4.3 percent on average, making the main contribution to APG. Resource reallocation also contributed positively by adding 1.2 percent to APG on average during the period. Net entry added 0.3 percent to APG on average. Over the period, APG shows a declining trend after peaking at a growth rate of 11 percent in 2004. I find that the main driver of the decline is the sharp decrease in technical efficiency growth. Moreover, despite the fact that the effect of resource reallocation increased APG after the 2008 global financial crisis, technical efficiency growth fell sharply causing APG to decline. Similar to the pattern found in the manufacturing industry, most of the two-digit industries in manufacturing experienced a slowdown in APG. However, the contribution of technical efficiency and reallocation differed across industries. APG was negative in recent years in the cases of the Basic Metal Products and Other Transport Equipment industries, where the necessity of industrial restructuring was strongly urged to strengthen competitiveness.
There are recent papers which apply the same measure of APG from Petrin and Levinsohn (2012) to study the effects of resource allocation and technical efficiency growth on APG. Petrin, White and Reiter (2011) find a 2.2% rate of APG on average in the U.S. manufacturing industry between 1976 and 1996. They show that resource reallocation effects contributed mainly to APG. For manufacturing in Japan, Kwon, Narita and Narita (2015) show that resource reallocation effects decreased in the 1990s and impacted APG negatively during the late 1990s.
Several studies used alternative measures of aggregate productivity growth for the Korean manufacturing industry. These measures define aggregate productivity growth based solely on plant-level technical efficiency. Baily, Hulten and Campbell (1992) (BHC) and Foster, Haltiwanger and Krizan (2001) are examples of studies which use this measure. Hahn (2003) finds that plant entries and exits account for 45 percent of manufacturing productivity growth during the 1990-95 cyclical upturn and for 65 percent during the 1995-98 downturn. He also shows that resource reallocation contributed negatively during the 1990-95 upturn but positively during the 1995-98 downturn. Ahn (2006) finds a large role of the net entry of plants at a similar magnitude to APG between 1990 and 2003. The measured contribution of net entry is sensitive to the length of the period in the analysis because the longer the period, the higher the number of plants which are counted as entering and exiting. The measured contributions of technical efficiency, reallocation, and net entry to APG in these papers are different from the results of this paper. These differences are not only the result of the different periods of analysis but are also due to the methods applied to measure APG. When I estimated APG using the method devised by BHC, I found that the levels of variance in the reallocation effects and net entry effects are large for the BHC measure. Moreover, BHC resource reallocation effects were negative while PL resource reallocation effects were positive on average throughout the period. These findings imply the necessity of a cautious approach when studying the roles of technical efficiency, reallocation, and net entry, as the results depend on how APG is defined.
Among the many sources of the decline in APG, this paper focuses on productivity growth at young plants. Young plants contribute substantially to the creation of jobs and in creating value-added. Recent research has uncovered the importance of the role of a firm's age. For example, Haltiwanger, Jarmin, and Miranda (2013) find that surviving young firms show considerably higher growth rates than mature firms. Haltiwanger, Jarmin, Kulick and Miranda (2016) find that young firms undergoing high growth contribute to job creation and output growth disproportionately more relative to their share in employment and output. Both papers analyze the U.S. economy using data that covers firms and plants in the U.S. private sector.
For the Korean economy, Pyo, Hong, and Kim (2016) and Cho, Chun, Kim, and Lee (2017) study the roles of age and size on job creation. Both papers utilize Census on Establishment data, which covers all establishments. Pyo, Hong, and Kim (2016) find while controlling for firm size that younger firms show higher net job growth rates. Cho, Chun, Kim, and Lee (2017) show that establishment births explain the majority of job creation among small businesses, which themselves account for the majority of job creation. However, they find no systematic relationship between age and job creation, except with regard to births. In this paper, I study the role of young plants on productivity growth in the Korean manufacturing sector.
The role of young plants can be found in many important outcomes. However, the share of young plants in Korean manufacturing has been declining over the past two decades. The proportion of young plants dropped from 45% in 1995 to 28% by 2013, while the shares in employment and value-added both dropped in a similar fashion. As a result, the average age of manufacturing plants has increased over the last twenty years. This declining pace of dynamism is likely to have affected the decline of APG. Section IV measures the productivity growth of young plants and identifies the causes of the decline. Furthermore, I analyze the contribution of young plants in high-tech manufacturing industries.
To quantify the impact of young plants on APG, I define young plants as plants aged up to five years old and aggregate the contribution of each young plant to APG. First, I show that young plants account for nearly half of APG (48%), while their share with regard to value-added is 14 percent on average between 1995 and 2013. During the same period, small plants with less than 300 employees represent 36 percent of APG while their share of value-added is 47 percent. Second, productivity growth of young plants shows less variation than that associated with APG and increases APG during economic recessions. Third, productivity growth of young plants has been declining for the last ten years and has thus not boosted productivity growth as much during that time.
The declining growth rate of young plants may have resulted from fewer entries or from the lower growth rates of young plants. When I decomposed the effects of young plants into the effects of entries and the effects of continuing young plants, I found that the effects of young plants were reduced mainly due to lower growth rates of continuing young plants. The growth rates of continuing young plants are lower in the most recent ten years than in the previous ten years. This period corresponds to the period during which the Korean government implemented active start-up support policies and greatly increased the budget size for the policies. It is necessary to understand the business dynamics when designing an effective start-up policy.
Moreover, I find that the APG of the high-tech industry decreased in the last three years, while the effects of young plants on productivity growth in the high-tech industry were sharply reduced over the last three years. This is linked to the sharp decline in the APG of manufacturing in the last three years, as the APG of the high-tech industry accounts for major part of APG overall. High-tech industries are among those focused on by the government, which considers them an engine of future growth. Fewer entries and lower growth rates of plants in these industries could limit productivity growth in the manufacturing industry.
This study has a few limitations regarding the data used to measure APG and the effects of young plants. I use plant-level data from 1995 to 2013 from the annual Mining and Manufacturing Survey provided by Statistics Korea. This survey covers all establishments with ten or more employees. The majority of plants have fewer than ten employees, and their impacts are not measured. With regard to these young plants which are more likely to start their business with fewer than ten employees, the effects of these plants can be underestimated relative to their actual role. Nevertheless, gross output produced from the plants covered in the survey accounts for 87% of the gross output of manufacturing in 2012, where the gross output data is obtained from the national input-output table from the Bank of Korea.
Another limitation is that the unit of analysis is at the establishment level and not at the firm level. When an existing firm establishes a new plant to expand its business, the plant is considered as young given that it was created at that point, with the age of the existing parent firm disregarded. Thus, some of the effects of young plants come from new plants established by existing firms. However, an establishment-level analysis has the advantage of having well-defined units of businesses with employees. A firm-level analysis can contain effects coming from acquisitions and mergers, thus blurring the relationship between firm growth and age.
The next section introduces the methodology used to measure APG and how this data was decomposed. It also explains the plant-level data. Section III presents the results. Section IV discusses the productivity growth of young plants. Section V concludes the paper.
II. Measuring Aggregate Productivity Growth
A. Aggregate Productivity Growth
I use the definition of aggregate productivity growth (APG) by Petrin and Levinsohn (2012) (PL) to measure aggregate productivity growth in the Korean manufacturing industry between 1995 and 2013. APG is defined as the change in aggregate final demand net of the change in the expenditures on labor and capital. Plant-level data is utilized to construct the APG measure. Any changes in each plant’s technical efficiency or in a reallocation of inputs across plants contribute to APG according to this definition.
In addition to this method, there are other methods which can be used to measure APG, for instance by aggregating individual plants’ productivity, as was done by BHC. They measure APG according to the change in the weighted average of plant-level technical efficiency. Numerous papers which measure APG in the Korean manufacturing industry are based on these methods (e.g., Hahn, 2003; Ahn, 2006; Rhee and Pyo, 2015). Petrin and Levinsohn (2012) discuss the problems which can arise when measuring APG with the BHC method.
One problem is that APG can increase in some cases when using the BHC method while aggregate output decreases due to the reallocation of inputs across plants. These cases can arise if the value of the additional output net of the increased cost of input decreases while the inputs are reallocated across plants. BHC reallocation effects can be positive in these cases if inputs are reallocated to plants with higher levels of technical efficiency, as the definition by BHC of reallocation effects uses only technical efficiency as weights to the change in input. The definition of reallocation effects in APG uses the differences between the marginal product and the unit cost of the input as weights to the change in input.
Another problem is that the estimated effects of the reallocation of inputs are excessively large and various. This problem stems from the large dispersion of the estimated technical efficiency among plants. Petrin and Levinsohn (2012) overcome these problems by defining APG and reallocation effects such that APG decreases when there is a loss in output and reallocation effects capture the difference in the value of the marginal product and input cost. In this paper, I apply both methods, PL and BHC, using micro-level data pertaining to Korean manufacturing to study the roles of technical efficiency and reallocation in APG. The results from the two methods are compared.
APG represents the change in the aggregate final demand net of the change in the expenditures on inputs. It is expressed by the following equation,
where dYi is the change in the final demand of plant i ’s output, and Pi is the price of the output. dXif denotes the change in plant i ’s primary input f , and Wif is the unit price of the input. Labor and capital can be considered as primary inputs. The time index is suppressed for convenience.
There is no available data with which to distinguish how much of each plant’s output is spent on final demand. The growth accounting identity requires aggregate final demand to be equal to aggregate value-added,
where VAi is the value-added of plant i .
The growth accounting identity is utilized to express APG, as follows:
Here, dVAi is the change in the value-added of plant i .
Using Eq. (3), APG is calculated by aggregating the value-added and expenditure on inputs by individual plants. Given the way in which APG is defined, we can measure each plant’s contribution to APG and analyze the effects of a group with particular characteristics.
PL represents the decomposition of APG into its technical efficiency and reallocation components. Kwon, Narita, and Narita (2015) undertake a further decomposition of APG into the technical efficiency effect (TE), resource reallocation effect (RE) and net entry effect (NE). I use their decomposition of APG and the following notations for each component:
Here, ln Ait is the log TFP of plant i . Dit denotes the Domar (1961) weight, which is equal to the gross output of plant i over the aggregate value-added. A bar over a variable indicates an average over two
periods of time 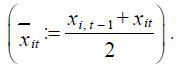 Ct is the set of continuing plants which are active for year t −1 and year t.
Ct is the set of continuing plants which are active for year t −1 and year t.
The technical efficiency effect is the contribution to APG due to the changes in plant-level technical efficiency. TE is the sum of the weighted plant-level technical efficiency, where the weight is the ratio of each plant’s gross output to aggregate final demand. The plant-level technical efficiency estimate is obtained by estimating a production function. I use gross output production to consider a plant’s usage of intermediate inputs in the estimation. It is natural to use a plant’s gross output when weighting for this specification. Petrin and Levinsohn (2012) find a rationale for using the Domar weight from Hulten (1978), holding that the contribution of the plant-level technical efficiency gain is identical to additional output multiplied by the price of the output.
In this equation, εif if is the elasticity of output with respect to input f , and sif is the ratio of expenditures on input f to gross output of plant i . Δln Xift is the log change in input.
The difference between the marginal product and the unit cost of input f , i.e., (εif − sift), is weighted to the change in input. Reallocation effects exist only when there is a difference between the two. Reallocation effects aggregate the changes in output due to the reallocation of inputs across plants. There is a gain in allocative efficiency when inputs move from plants with a lower marginal product to a higher marginal product relative to their unit cost of input.
Here, E and X indicate the sets of entering and exiting plants, respectively.
Net entry effects capture the net output minus the net unit costs of the input according to the net entry of plants.
Compared to the APG measure and its decomposition as introduced in this section, I present the BHC measure of aggregate productivity growth and its decomposition. Petrin and Levinsohn (2012) provide a detailed discussion of the difference between these two methodologies. BHC define aggregate productivity by the weighted average of plant-level technical efficiency. Aggregate productivity growth is the change of the weighted average. Following Petrin and Levinsohn (2012), the BHC aggregate productivity growth is approximated with discrete data, as follows:
Most empirical papers use labor or gross output shares as weights for technical efficiency. Petrin and Levinsohn (2012) used the Domar weight in the BHC measure to abstract from the difference in the technical efficiency effect using identical weights for both APG and BHC. In this paper, I used gross output shares as weights in the BHC measure to compare APG with other empirical results under the BHC framework. Thus, I allow technical efficiency effects to differ across the two measures. The Domar weight equals the gross output share only when there is no intermediate input use. Because APG uses the Domar weight, technical efficiency growth in APG will be larger than the BHC technical efficiency growth when there is more intermediate input use.
The resource reallocation effect and net entry effect when using the BHC measure are expressed as follows:
B. Data and Estimation
I utilize plant-level data from 1995 to 2013 from the annual Mining and Manufacturing Survey provided by Statistics Korea. Only the manufacturing sector is considered. The survey covers all establishments with ten or more employees. The survey classifies plants according to the five-digit Korean Standard Industry Classification (KSIC). KSIC was revised three times, from Rev. 6 to 9, during the period of analysis. I used concordance tables from Statistics Korea to match industries to KSIC Rev. 9.
The set of plants used in the analysis includes 52,391 plants in 1995, increasing to 64,332 plants in 2013. I compared the number of plants and the aggregates of gross output and employees respectively in the set with statistics on sectoral output and employee data in 2012 from the Bank of Korea. The set represents 17% of the number of plants, 87% in terms of gross output, and 72% in terms of employees. The coverage with regard to the number of plants is low because the majority of plants hire fewer than ten employees. However, relatively large plants account for most of the gross output and employees in the manufacturing industry.
I use information on the number of employees, gross output, capital stock, total expenditures on intermediate inputs, and wages from the survey. The expenditures on intermediate inputs include the costs of materials, fuel, electricity, water, and processing costs paid to subcontractors. I define capital stock as the sum of the average book value of the building structure, machinery, and transport equipment between the beginning and end of the year.
What we observe in the data are in nominal values. I calculated industry-level deflators at the two-digit level using gross output and intermediate input data both in nominal and real values from the productivity database of the Korea Productivity Center. Constructed deflators are gross output deflators and intermediate input deflators for 19 industries in manufacturing. I deflate the nominal value of each plant’s gross output and expenditures on intermediate inputs using these deflators. Real value-added is defined as the real value of gross output minus the real value of expenditures on intermediate inputs. For capital stock, I constructed deflators for building structures, machinery, and transport equipment using gross capital formation in national accounts in nominal and real values provided by the Economic Statistics System of the Bank of Korea. Real capital stock is the sum of the real values of each fixed asset. Real wage is obtained using the consumer price index (CPI) from the Bank of Korea.
These real values constructed from plant-level data are used to calculate APG and its decomposition in Eqs. (3)-(7). All terms in the equations except for technical efficiency ( Ait ) and the elasticity parameters ( εif ) are directly obtained from the data. I use the following gross output specification of the Cobb-Douglas production function,
where Qit is the gross output of plant i , and Kit , Lit and Mit are the capital, employees, and intermediate inputs, i.e., the production inputs of plant i . εjK , εjL , εjM are coefficients in the estimation, representing the elasticities of each production input.
I estimate the elasticity parameters for all 82 three-digit industries using the estimation method by Wooldridge (2009). The method is based on Levinsohn and Petrin (2003), who use intermediate inputs to control the simultaneity problem arising from the correlation between unobserved productivity and the input level. Wooldridge (2009) proposes the use of a generalized method of moments (GMM) framework. He shows that the method is robust to the identification problem1 that can arise when applying the two-step estimation method of Levinsohn and Petrin (2003). In this paper, I used one- and two-year lag variables of labor and intermediate inputs as instrumental variables. Once the elasticity parameters are estimated, Eq. (11) is used to calculate plant-level productivity.
III. Aggregate Productivity Growth
This section presents the measured aggregate productivity growth of the Korean manufacturing industry and its decomposition. I compare the baseline results from the PL method to the results from the BHC method. This section also reports APG and its decomposition for industries at the two-digit level.
A. Aggregate Productivity Growth and its Decomposition
Table 1 reports annual APG and its decomposition between 1995 and 2013. The average APG is 5.7 percent during this period. Technical efficiency effects account for a larger part of APG than resource reallocation effects and net entry effects.
TABLE 1
APG AND ITS DECOMPOSITION
Note: The growth rates for 2010 and 2011 are the average annual growth rate between 2009 and 2011.
Source: Author’s calculation from the Mining and Manufacturing Survey.
Except for the rebounding growth rate after two economic crises of 1998 and 2009, APG declines from a peak of 11 percent in 2004. I divided the period from 1995 to 2013 into the first ten years and the last ten years to compare the average growth rates for each period, finding that APG declined from 6.9 percent in the first ten years to 4.5 percent in the last ten years. The main reason for the decline comes from the rapid drop in the technical efficiency effects. Technical efficiency effects dropped from 6.8 percent in the first ten years to 1.8 percent in the last ten years. The 4.5 percent average rate of APG in the last ten years was mainly attributable to resource reallocation effects. For the more recent three years between 2011 and 2013, APG showed less than a 1 percent growth rate. Both technical efficiency effects and net entry effects made negative contributions to APG during this period.
Some recent work investigated the role of resource reallocation in industry-level productivity growth during recessions. Focusing on the U.S., Foster, Grim and Haltiwanger (2016) show that the role of reallocation in enhancing productivity was reduced during the Great Recession compared to the previous recession. Table 1 shows that resource reallocation effects helped to increase APG continuously in the five years after the global financial crisis. Despite the positive resource reallocation effects during this period, technical efficiency effects fell sharply, lowering APG.
Table 1 presents the baseline results from the PL method. Many papers (e.g., Hahn, 2003; Ahn, 2006) used annual Mining and Manufacturing Survey to measure aggregate productivity growth based on the BHC method. To show empirical differences between the PL method and the BHC method, I calculated BHC aggregate productivity growth using Eqs. (8), (9) and (10). I used gross output shares as weights. I present the empirical differences between PL and BHC in Appendix A.
The results show that the degrees of variance in the reallocation effects and the net entry effects are large for the BHC measure. For nearly half of the twenty-year period, the resource reallocation effects of PL and BHC show opposite signs. On average, BHC resource reallocation effects were negative while PL resource reallocation effects were positive. The difference is large, particularly for years after 2008 global financial crisis. These findings suggest that the measured aggregate productivity growth and its decomposition into technical efficiency, reallocation, and net entry are sensitive to the method applied.
B. Sectoral Productivity Growth and its Decomposition
In this subsection, I study the contribution of each sector to APG in the manufacturing industry. I also study whether the source of the productivity growth differs across industries by calculating APG decompositions. Table 2 presents sectoral productivity growth and its decomposition for industries at the two-digit level. Using the given definition of APG, we can easily compute the contribution of each individual plant to APG. Sectoral productivity growth is defined by aggregating the contribution of each individual plant by sector. The weight in the aggregation is the Domar weight defined for industries at the two-digit level, i.e., the gross output of individual plants over sectoral value-added.
Table 2 lists the sectors according to the size of the average value-added share. The first column in Table 2 shows that sectoral productivity growth differs considerably across sectors. The designation Electronic Components, Computer, Radio, Television and Communication Equipment creates 21 percent of value-added on average in the manufacturing industry and shows the highest average growth rate. Among the top ten industries in terms of the value-added share, the lowest and the second lowest growth rates were found in the Basic Metal Products and Other Transport Equipment industries, where the necessity of industrial restructuring was strongly urged to strengthen competitiveness.
TABLE 2
APG AND ITS DECOMPOSITION FOR INDUSTRIES AT THE TWO-DIGIT LEVEL
Note: The growth rates for 2010 and 2011 are the average annual growth rate between 2009 and 2011.
Source: Author’s calculation from the Mining and Manufacturing Survey.
Looking at the average contribution of technical efficiency, reallocation and net entry, different sectors have different relative factors of productivity growth. Out of top ten value-added share industries, four industries (26, 24, 29, 22) make relatively large resource reallocation contributions, while the other six industries (30, 20, 10, 25, 31, 28) have larger contributions of technical efficiency.
Figures 3 and 4 show the sectoral productivity growth estimates and related components for industries 26 and 30, respectively. These two sectors account for 32 percent of value-added in the manufacturing industry. The factors that help to increase productivity growth stand in contrast between the two sectors. For industry 26, reallocation effects were positive for most years during the period of 1995-2013. The recent slowdown in productivity growth was affected by negative effects of technical efficiency. In contrast, technical efficiency effects were the main driver of productivity growth in industry 30 and negative reallocation effects decreased the productivity growth during the most recent four years.
IV. The Role of Young Plants in Aggregate Productivity Growth
This section empirically shows the role of young plants in aggregate productivity growth. Figure 5 shows the share of young plants (less than six years old) in terms of the number of plants, employment, and value-added for all plants with ten or more employees in the Mining and Manufacturing Survey. The share of young plants in the manufacturing industry shows a decline for all three variables over the last twenty years. The declining share of young plants is likely to have affected aggregate productivity growth.
FIGURE 5.
SHARE OF YOUNG PLANTS
Note: The graph shows the share of young plants (less than six years old) in terms of the number of plants, employment, and value-added.
Source: Author’s calculation from the Mining and Manufacturing Survey.
A. Young Plants’ Contribution to Aggregate Productivity Growth
In this section, I compute the contribution by young plants to aggregate productivity growth. I define young plants as plants up to age 5 in the baseline results. Results for young plants up to age 2 are presented to study the effects of start-ups. I use the establishment year information in the Mining and Manufacturing Survey to calculate plant ages. Using the definition of APG in Eq. (3), the contribution by young plants to APG ( APGyoung ) is measured as follows:
The contribution of old plants to APG ( APGold ) is defined correspondingly. APG is the sum of APGyoung and APGold .
Figure 6 shows the estimates of APG and the contributions by young and old plants for the period of 1995-2013. Table 3 reports the average of those estimates. There are three main findings regarding the role of young plants in aggregate productivity growth. First, the contribution of young plants to APG is much larger than their shares for value-added. Productivity growth by young plants accounts for nearly half of APG on average over the twenty-year period while their valued-added share is only 14 percent on average. Young plants show high growth in value-added relative to growth in input expenditures. Second, productivity growth of young plants shows much less variance than that of APG, and it increases APG during economic recessions. Third, young plants’ productivity growth shows a decline over the last ten years. A decline is apparent for the last three years of the period of analysis. The last two columns in Table 3 decompose productivity growth by young plants into the growth of start-ups (age 0-2) and the growth of young plants (age 3-5). These results show that productivity growth declines in the last ten years for both start-ups (age 0-2) and young plants (age 3-5).
FIGURE 6.
APG AND ITS DECOMPOSITION INTO DIFFERENT AGE GROUPS
Note: The growth rates for 2010 and 2011 are the average annual growth rate between 2009 and 2011.
Source: Author’s calculation from the Mining and Manufacturing Survey
TABLE 3
APG AND ITS DECOMPOSITION INTO DIFFERENT AGE GROUPS
Source: Author’s calculation from the Mining and Manufacturing Survey.
To compare the size of the contribution from young plants to that of small plants, I compute the contribution of small plants to APG by applying Eq. (12) to plants with less than 300 employees. Table 4 presents the results. During the twenty-year period, small plants with less than 300 employees account for 36 percent of APG while their share in value-added is 47 percent on average. Productivity growth rates decline for both large and small plants in the last ten years, with a remarkably steep decline for large plants over the last three years.
The fourth column in Table 4 shows the productivity growth of young plants among the small plants. I find that young plants contribute to the majority of small plants’ productivity growth. I also find that the productivity growth of small and young plants did not decline much compared to the decline in APG. These results imply that the steep decline in the productivity growth of young plants was due to large and young plants.
B. Continuing, Entering and Exiting Plants
The declining productivity growth of young plants may have resulted from fewer entries or from the lower growth rates of young plants. Table 5 shows the decomposition of the productivity growth of young plants into the effects of net entries and the effects of continuing young plants. The productivity growth of young plants was reduced mainly due to the lower growth rates of continuing young plants. The recent ten-year period corresponds to the period when the Korean government implemented active start-up support policies and greatly increased the size of the budget related to these policies. These results imply certain policies can effectively increase aggregate productivity growth if those policies can help surviving start-ups to grow rather than focus only on increasing the number of start-ups.
C. Plants Age and Productivity Dynamics
Both the decrease in the growth rate of technical efficiency and the decrease in the share of young plants can be responsible for the slowdown in productivity growth by young plants. I investigate whether the changes in the technical efficiency of young plants or the changes in their shares have affected productivity growth. To this end, I compare the simple average and the weighted average of technical efficiency for each age group. Figure 7 shows the time-series unweighted mean of plant-level technical efficiency by age group during the period of 1995-2013. The values are relative to the mean of plants over 11 years old. At the beginning of the period, there was little difference in average productivity by age group. For the 0-2 age group, the productivity level drops relative to that of the oldest group during five years after the Asian financial crisis. From 2003, the relative productivity level of 0-2 age group increased, not showing a great difference relative to that of the oldest group until 2007. From 2008 onward, the relative productivity levels of young group of plants (the 0-2 and 3-5 age groups) exceed those of the oldest group. The relative slowdown in the productivity growth of old plants after the global financial crisis may account for this difference. It may also come from a selection effect, in that only highly productive young plants entered the market.
FIGURE 7.
(UNWEIGHTED) AVERAGE PRODUCTIVITY BY DIFFERENT AGE GROUPS
Note: The graph shows the unweighted mean of plant-level technical efficiency. For each year, values are reported relative to the age group for plants older than 10.
Source: Author’s calculation from the Mining and Manufacturing Survey
Despite the fact that the average productivity of young plants increased relative to that of old plants after 2008, their weighted average productivity rates did not increase. Figure 8 shows the weighted mean of plant-level technical efficiency by age group for each year using the Domar weight. The weighted mean of technical efficiency is larger for the older group, and the difference in magnitude is much greater for the weighted mean than for the unweighted mean. Relative productivity of young plants shows a decline over twenty years, reaching 5 percent of the oldest group since 2011. The decline was steeper for the 3-5 age group. These results imply that the declining share of young plants contributed to the decreased productivity growth of young plants.
FIGURE 8.
(WEIGHTED) AVERAGE PRODUCTIVITY BY DIFFERENT AGE GROUPS
Note: The graph shows the Domar-weighted mean of plant-level technical efficiency. For each year, values are reported relative to the age group for plants older than 10.
Source: Author’s calculation from the Mining and Manufacturing Survey.
D. Contribution of Young Plants in the High-Tech Industry
In this section, I look at the productivity growth of the high-tech sector to determine whether the growth rates show the same pattern across sectors with different tech levels. I focus on the high-tech sector because this sector contributed most to productivity growth over the last twenty years. The high-tech sector is among those targeted by the Korean government in their recent policy goal of preparing for the ‘Fourth Industrial Revolution’. I also analyze the contribution of young plants in high-tech manufacturing industries.
I follow Ahn (2006) when categorizing industries according to the intensity of the technology used in them. He used OECD methodology to classify industries into four sectors and studied productivity growth in each sector. The OECD uses the R&D investment share of value-added or output for technology intensity classification purposes. I match industries with the OECD (2011) technology intensity classification defined in the International Standard Industrial Classification (ISIC) Rev. 3. Table A2 in the appendix lists the industries for each technology classification based on KSIC Rev. 9.
Tables 6 and 7 report the decomposition of APG and young plants' productivity growth, respectively, into four sectors based on the technology intensity level. The higher the technology intensity is, the higher the productivity growth rate becomes. The two sectors of high technology and medium-high technology account for 80 percent of APG on average. I find that over the last three years, the productivity growth rates of high-tech industries decreased and that the productivity growth rates of young plants in high-tech industries declined sharply. This is associated with the sharp decline in the APG of manufacturing for the last three years given that high-tech industries account for a major portion of APG. High-tech industries are also among those targeted by government policies as an engine of future growth. Fewer entries and lower growth rates of plants in these industries could limit productivity growth in the manufacturing industry.
TABLE 6
APG AND ITS DECOMPOSITION INTO DIFFERENT TECH SECTORS
Note: Industries (KSIC Rev. 9) are matched to the OECD (2011) tech level classification defined in the International Standard Industrial Classification (ISIC) Rev. 3.
Source: Author’s calculation from the Mining and Manufacturing Survey.
TABLE 7
YOUNG PLANTS’PRODUCTIVITY GROWTH IN DIFFERENT TECH GROUPS
Note: Industries (KSIC Rev. 9) are matched to the OECD (2011) tech level classification defined in the International Standard Industrial Classification (ISIC) Rev. 3.
Source: Author’s calculation from the Mining and Manufacturing Survey.
V. Concluding Remarks
In this paper, I adopted the method devised by Petrin and Levinsohn (2012) to measure aggregate productivity growth. I reported that both aggregate productivity growth and that the productivity growth of young plants decelerated over the last ten years, i.e., between 2004 and 2013. The findings in this paper stress the important role of young plants in aggregate productivity growth. Understanding the dynamics of young plants is necessary to form effective start-up policies. The Korean government implemented active start-up support policies and greatly increased the size of the budget over the past ten years. I discuss several policy implications based on the results of this study.
I found that productivity growth by young plants accounts for nearly half of APG on average over the twenty-year period, while their valued-added share is only 14 percent on average. In contrast, SMEs account for much less in terms of APG relative to their share. Though the role of young plants in creating jobs is not measured in this paper, recent studies (e.g., Pyo, Hong, and Kim, 2016; Cho, Chun, Kim, and Lee, 2017) find an important role of young firms in job creation in Korea. Many policies are oriented to support small and medium-sized enterprises (SMEs). When the goal of such policies is to help economic growth or to create jobs, policymakers must consider the important role of age.
Even when policies target young enterprises, they need to be designed based on an understanding of the dynamics of young plants. The results of this study show that productivity growth by young plants mostly occurs in plants up to three years old. The Korean government has already implemented policies to lower start-up costs, such as R&D support and government lending. It is advisable to check whether these resources are allocated to high growth establishments. Recent research (e.g., Haltiwanger, Jarmin, Kulick and Miranda, 2016) shows that only a small number of young firms grow rapidly and make a disproportionate contribution to growth. Understanding the characteristics of these high-growth young firms can help in the creation of selection criteria for government programs.
I also found that the decline in the productivity growth of young plants (age 4-5) contributed substantially to the decline in the productivity growth of young plants (age 0-5) over the last ten years. The Small and Medium Business Administration in Korea implemented a program starting in 2015 which supports young establishments between three to six years of age to increase their revenue. This program will be effective when it helps entrepreneurs to overcome difficulties stemming from market failures. This is true for other policies that support entrepreneurs as well.
Further analysis is needed to identify and measure difficulties that entrepreneurs and young establishments face when their start up their businesses and grow. I showed that the productivity growth rates of young plants in high-tech industries sharply declined over the last three years. Probing the reasons why young plants in high-tech industries could not grow can provide implications for Korean policies intended to foster a new growth engine.
APPENDIX
A. Comparing APG to the BHC APG measure
Table A1 and Figure A1 compare the BHC APG estimates to the (PL) APG estimates. The dots in Figure A1 are the growth rates of value-added. APG closely follows the growth rates of value-added because APG is defined as the growth rate of value-added minus the growth rate of expenditures on labor and capital. For many years, BHC APG is smaller than the APG estimates. On average, APG is approximately three times larger than BHC APG (5.7 versus 1.8).
TABLE A1
COMPARING APG AND ITS DECOMPOSITION TO THE BHC MEASURE
Note: The growth rates for 2010 and 2011 are the average annual growth rate between 2009 and 2011.
Source: Author’s calculation from the Mining and Manufacturing Survey.
FIGURE A1.
COMPARING APG (BASELINE) AND BHC APG
Note: The growth rates for 2010 and 2011 are the average annual growth rate between 2009 and 2011.
Source: Author’s calculation from the Mining and Manufacturing Survey.
A large part of the difference between the two measures is due to the different weights used in each measure. By definition, APG technical efficiency growth (TE) and BHC technical efficiency growth (BHC TE) differ only in terms of the weights used when aggregating technical efficiency growth. The estimated TE showed much larger growth at 4.3 percent on average than BHC TE, which showed 1.7 percent.
Figure A2 compares the estimates of the resource reallocation effects and net entry effects between the two methods. A few differences become apparent. First, BHC reallocation effects and BHC net entry effects show much larger degrees of variance than those of APG. Second, the estimates of resource reallocation effects frequently show opposite signs for a given year (for 9 years out of 20 years). For the years after the 2008 global financial crisis, reallocation effects were positive in APG, whereas BHC reallocation effects were negative. This comparison of the results shows that the estimates of APG and its components can differ remarkably depending on the method used.
B. Technology Classification of Industries
Table A2 lists the industries for each technology classification based on KSIC Rev 9. Industries (KSIC Rev. 9) are matched with the OECD (2011) technology intensity classification as defined in the International Standard Industrial Classification (ISIC) Rev. 3.
TABLE A2
TECHNOLOGY CLASSIFICATION OF INDUSTRIES
Source: OECD. 2011. “ISIC REV. 3 Technology Intensity Definition.” OECD Publishing, Paris.
References
, , , & . (2017). Job Creation and Destruction: New Evidence on the Role of Small versus Young Firms in Korea. The Japanese Economic Review, 68(2), 173-187, https://doi.org/10.1111/jere.12133.
(1961). On the Measurement of Technological Change. Economic Journal, 71, 709-729, https://doi.org/10.2307/2228246.
, , & . (2016). Reallocation in the Great Recession: Cleansing or Not? Journal of Labor Economics, 34(1), 293-331, https://doi.org/10.1086/682397.
, , & . (2013). Who Creates Jobs? Small versus Large versus Young. The Review of Economics and Statistics, 95(2), 347-361, https://doi.org/10.1162/REST_a_00288.
(1978). Growth Accounting with Intermediate Inputs. Review of Economic Studies, 45, 511-518, https://doi.org/10.2307/2297252.
, , & . (2015). Resource Reallocation and Zombie Lending in Japan in the 1990s. Review of Economic Dynamics, 18, 709-732, https://doi.org/10.1016/j.red.2015.07.001.
, , & (2011). The Impact of Plant-level Resource Reallocations and Technical Progress on U.S. Macroeconomic Growth. Review of Economic Dynamics, 14, 3-26, https://doi.org/10.1016/j.red.2010.09.004.
, & . (2012). Measuring Aggregate Productivity Growth Using Plant-level Data. The RAND Journal of Economics, 43(4), 705-725, https://doi.org/10.1111/1756-2171.12005.
(2009). On Estimating Firm-level Production Functions Using Proxy Variables to Control for Unobservables. Economics Letters, 104(3), 112-114, https://doi.org/10.1016/j.econlet.2009.04.026.