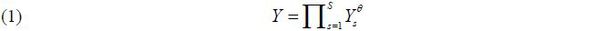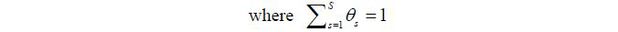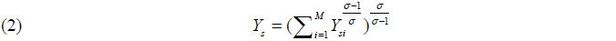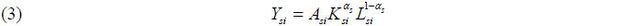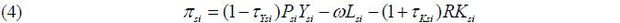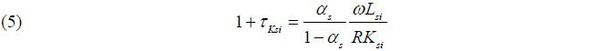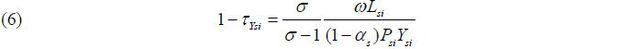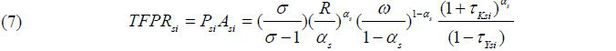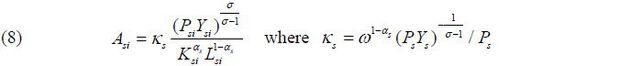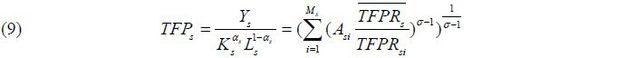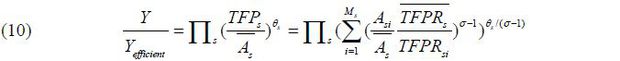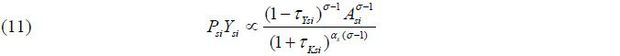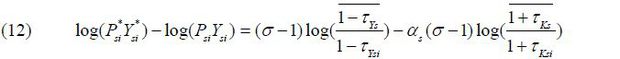Misallocation and Manufacturing TFP in Korea
Abstract
This paper analyzes the effects of allocative efficiency on productivity in the manufacturing sector of Korea following Hsieh and Klenow (2009). The results of this research indicate that the overall allocative efficiency declined from 1990 to 2012. Using the method of Oberfield (2013), which allows inter-industry resource movement as well as intra-industry reallocation, we confirm that intensified misallocation generally results from intra-industry allocative inefficiency. The potential loss from instances of worsening misallocation is estimated to be approximately 0.6% points for each year, which is considerable in terms of the overall TFP. In terms of the firm size distribution, initially large establishments are more likely to expand if distortions are removed in most countries. One notable feature in Korea is that this pattern is pronounced. This implies that subsidies to unproductive small-sized establishments are heavily implemented.
Keywords
Misallocation, Productivity Differences, Misallocation by Establishment Size
JEL Code
O11, O47, O53
I. Introduction
Productivity differences have received attention as a principal source of the gap between rich and poor countries. There are two main directions of research on productivity. Traditionally, many studies compare the productivity growth of a representative (average) firm for each country. Growth accounting is a typical strategy used in this strand. Another approach focuses on the heterogeneity of firms or industries and pays attention to allocative efficiency. The distribution of firm productivity within the same industry is known to be highly dispersed; thus, resource redistributions toward more productive cases generates higher TFP growth throughout the economy, even if the productivity level of each firm does not change.
Emphasizing allocative efficiency has been a growing trend and is currently popular. Hsieh and Klenow (2009, HK henceforth) developed an empirical methodology for measuring TFP losses due to instances of resource misallocation. They compared the extent of misallocations for the U.S., China, and India using plant-level data from the manufacturing sector of each country. In the absence of misallocation, the U.S. can achieve an increase of output of approximately 30-43%, while China and India can enjoy rates of 87-115% and 100-128%, respectively. What they refer to as “misallocation” roughly alludes to inefficiency, which is measured as the ratio of current output relative to the potential output resulting from the removal of exogenous distortions. This potential output is hypothetically achieved in the absence of differences apart from productivity differences. Each firm/plant differs in terms of their technology or efficiency level when creating their products. Only in terms of productivity should the amount of factor inputs be distributed according to the relative order of firm productivity. In reality, this is not the case. All other factors affecting allocation except for productivity are regarded as distortions.
The HK methodology has several shortcomings; one of them is that it investigates allocative efficiency only within industries. In the HK method, the total amounts of capital and labor in each industry are fixed and do not very between industries. This weakness shuts down the flexibility of factor movement during industry-specific shocks. Oberfield (2013) developed a measure of allocative efficiency along the lines of Hsieh and Klenow (2009), allowing resource movement between industries. He found an interesting phenomenon during the 1982 crisis in the Chilean manufacturing sector. A severe contraction in output during this period is mostly accounted for by a falling Solow residual, and a decline in between-industry allocative efficiency contributes to the drop in TFP while the within-industry efficiency remains constant.
Following the HK methodology, observations from many countries were also reported. Using plant data from the French manufacturing sector, Bellone and Mallen-Pisano (2011) argued that allocative efficiency in France is comparable to that in the U.S. Particularly, Hosono and Takizawa (2012) reported that misallocation in the manufacturing sector in Japan has been deepening since the 1980s. The unique point in their paper is that it determined the time series of misallocation over time as well as the overall level of misallocation compared to those in other countries. For Japan, they showed that the improvement in the TFP would be 47% if misallocation disappears. Bartelsman et al. (2013), who developed their own criterion to quantify misallocation, showed that approximately 15% of TFP losses can be accounted for by distortions in resource allocation in the transition economies of Central and Eastern Europe.
In this paper, we quantitatively measure the extent of misallocation in the Korean manufacturing sector and compare it with those in other countries following the same methodology used by Hsieh and Klenow (2009). Although Midrigan and Xu (2009) have analyzed capital misallocation using the same data, their derivation of capital frictions is based on the assumption that other inputs such as labor and intermediate inputs are allocated efficiently without friction. The HK calculation considers labor misallocation as well as capital misallocation; thus, the efficient output differs from that of Midrigan and Xu (2009).
This study also shows how efficiency in this sector has evolved over the past 20 years. The time-series trend in allocative efficiency is another contribution of our paper compared to the data results by Midrigan and Xu (2009), who mainly pool all year-plant observations while focusing on cross-sectional variations of capital productivity. With regard to robustness checks, we will investigate our results through the lens of the methodology developed by Oberfield (2013).
The main results here are as follows. Korea’s average allocative efficiency is found to be lower than that of the U.S., higher than that of China, and similar to that of Japan. Allocative efficiency in the U.S. was 0.73 (highest) while that of China was 0.50 (lowest).1 The rates for Korea and Japan are similar at 0.65 and 0.68, respectively. Meanwhile, the time series shows that Korea’s allocative efficiency in the manufacturing has been trending downward since the 1990s. This downward trend in Korea is similar to that of Japan when it began to experience slowing growth in the 1990s. A downward trend consistently appears after allowing for inter-industry resource allocation.
The paper proceeds as follows. Section II describes the HK and Oberfield (2013) methodologies heavily relied on by the present paper. In Section III, we report the empirical results. Section IV briefly summarizes possible reasons for misallocation in the Korean manufacturing sector. Section V presents our concluding remarks.
II. Previous Methodology
In this section, we illustrate the backbone frames of Hsieh and Klenow (2009) and Oberfield (2013) which will be used for the empirical analysis here.
Hsieh and Klenow (2009) provide a quantitative methodology pertaining to the potential effect of resource misallocation on the aggregate TFP. In an economy with heterogeneous production units, aggregate TFP depends not only on the TFPs of individual production units but also on how the inputs are allocated across these production units. If firm productivity is the single factor of heterogeneity, it is natural for input resources such as capital and labor to be distributed according to productivity differences. However, if there are firm-level distortions which are not related to productivity, resource allocation may damage aggregate productivity via a process known as misallocation. In Hsieh and Klenow (2009), the reasons for distortions are not primarily studied, but the types of distortions noted are taxes and subsidies, financial friction, trade restrictions, capital rationing, a host of regulations associated with firm-size-dependent policies, industrial policies, and entry barriers. In other words, distortions are the reduced forms of all possible sources which generate resource misallocation other than productivity.
How can we measure distortions (wedge) in real data? Can we identify differences in firm productivity and firm distortions? The answers can be found based on a standard model of monopolistic competition with heterogeneous productivity. With the Cobb-Douglas production function and constant elasticity of substitution between differentiated goods, firm markup is fixed and equal to all firms. Thus, revenue productivity (the product of physical productivity and a firm’s output price) should be equal across firms in the absence of distortion. To the extent revenue productivity differs across firms, a measure of firm-level distortion can be recovered. Although industry variance with regard to physical productivity exists, industry variance in revenue productivity vanishes in the absence of distortion.
The details of Hsieh and Klenow (2009) are presented below. Goods markets consist of final goods and industry goods. A final good (Y ) is produced by a representative firm in a perfectly competitive final output market. Industry goods (Ys ) are aggregated by way of Cobb-Douglas production.
Industry output Ys is a CES aggregate of Ms differentiated products.
Because individual products are produced in a monopolistic competition market, price elasticity is always σ (> 1) regardless of the production volume, and the markup is σ / (σ − 1).
Firm production is determined with the Cobb-Douglas function with productivity , Asi capital Ksi and labor Lsi. Firm productivity Asi (physical productivity: TFPQ) differs across firms. Capital elasticity αs, determining the income shares of capital and labor, is equal across firms within an industry but may not be equal across firms between industries.
A firm pursues profit maximization, as expressed by (4). PsiYsi denotes revenue in this case. w and R are the wage rate and capital rental rate, which are identical for all firms. Output distortion τYsi and capital distortion τKsi are unique in this setup. These types of taxes represent the reduced forms of distortion faced by firms. τYsi alters the marginal productivity of capital and labor at the same proportion, but τKsi interferes with the relative marginal productivity of capital over labor.
From the perspective of first-order conditions, τYsi and τKsi can be viewed from several perspectives. As expressed by (5), we infer the presence of capital distortion τKsi when the ratio of labor compensation to the capital stock differs relative to what one would expect from the degree of output elasticity with respect to capital and labor. τKsi is positive in a firm paying higher capital costs, and τKsi is negative if the labor cost is relatively high. The ratio of the marginal productivity of labor relative to capital is different from the industry mean, and τKsi is not equal to zero. Similarly, output distortion is measured when labor’s share is different compared with what one would expect given the degree of industry elasticity of output with respect to labor. τYsi represents the extent of the deviation of marginal revenue labor productivity (1 − α)(PsiYsi / Lsi) from the wage rate σ / (σ − 1)w.
Additionally, τKsi and τYsi in equations (5) and (6) converge to the industry mean once a hypothetical reform transpires. Note that the industry means of the distortions in the real data do not have to be zero. Meaningful interpretations of τKsi and τYsi refer to how much they differ from the industry mean instead of focusing on the degrees of the absolute deviation from zero.
Calculated values of τKsi and τYsi are reflected in the revenue productivity TFPRsi. All other factors are common, but this is not the case for the last instance in (7). Even firm productivity Asi does not make a difference with regard to TFPRsi. In the monopolistic competition frame, a firm with high productivity wants to lower its prices to raise its quantity of sales; thus, productivity itself is irrelevant with reference to the product of price and productivity. Only (1 + τKsi)αs / (1 − τYsi) is the single factor generating the variance of TFPRsi within an industry.
The next hurdle is to measure the physical productivity Asi. This calculation is heavily dependent on the functional form of the CES aggregator of industry goods. With a strong assumption of the production form, physical productivity is recovered from the nominal output PsiYsi. Because 𝐊s is common to firms within an industry, it can be normalized as 1.
Industry TFP is given as in equation (9); it is produced by the sum of physical TFP(Asi) of each firm weighted by TFPRs / TFPRsi (deviation from the average industry TFPR). When an individual firm’s output and capital distortions (τKsi & τYsi) collapse to the average industry level, meaning a firm’s TFPRsi is equal to the industry , TFPRs the industry TFPs becomes equal to As = (∑Asiσ−1)1/σ−1.
With (9) and the formula of As, we can calculate the ratio of the current output (Y ) to the efficient output (Yefficient ) via equation (10).
We will make a comparison between the HK method and the reallocation effect. Before explaining reallocation effects in growth accounting, we assume that every firm has its own productivity level and that it is fixed. Essentially, the reallocation effect means that increasing the market share of a firm with higher productivity causes an economy-wide TFP improvement. The philosophy of the HK method is very similar to the basic concept of the reallocation effect except that it emphasizes firm heterogeneity caused not only by the firm’s own productivity but also by distortion. When the government gives a particular firm a subsidy for its final products or provides access to inexpensive money, the marginal cost of the firm decreases as well as output increases relative to firms with identical productivity levels. Differing from the reallocation effect, the HK method suggests a quantitative degree of output loss caused by distortion, as explained above. In other words, the HK method presents the potential output if the allocative efficiency is maximized in the absence of distortion.
There are several limitations which apply to the HK method. First, misspecification error is one of the most crucial limitations, as the HK method relies fairly thoroughly on functional forms. If each firm has different levels of production elasticity of capital (αsi ≠ αs) caused by a technical gap in firms, τKsi and τYsi measured by the HK methodology consider the technical gap as a distortion. In fact, allocative efficiency is not clearly related to the technical gap or to the capital elasticity of the firm. Even a social planner is not able to overcome this constraint of technological differences between firms. The assumption of identical markups for every firm also produces measurement error in reality; τYsi represents this gap when the firm’s markup differs according to size.
Second, as mentioned above, the HK method is available for measuring the efficiency of only intra-industry firms. Inter-industry reallocations of capital and labor are not allowed during an industry-specific shock. Depending on the industrial policy of the government, inter-industry resource allocations can be affected even when the efficiency of intra-industry firms is not influenced. The HK method cannot detect this type of inter-industry resource allocation. Considering that many emerging countries implement industrial policies, this shortcoming may be a crucial limitation when this method is applied to emerging countries.
Third, the HK method does not take entries or exits into account explicitly. According to the literature, the quantitative size of the extensive margin (entries and exits) on TFP is not negligible and is more important than the extent of the intensive margin (incumbent firms). Entries and exits are frequent in the manufacturing sector, and fluctuation in the TFPR variance can be affected by entries and exits. For instance, if increasing demand in a particular industry causes more firms to enter it, the TFPR variance can increase and result in an increase in misallocations in the HK method.
Oberfield (2013) partly overcomes these shortcomings of the HK methodology. Although Oberfield (2013) depends on functional forms and does not consider the effects of entries and exits, his methodology relaxes the strong assumption that each firm has the same elasticity of capital. An important improvement by the methodology of Oberfield (2013) is that the decomposition of intra-and inter-industry misallocation can be accomplished by allowing free movement of inputs between industries. The key is that input reallocation between firms depends not only on firm productivity Asi but also on the elasticity of capital αsi. This implicitly makes input movement between industries possible.
III. Empirical Results
In this section, we use survey data from the mining and manufacturing industries supplied by the Korea statistics office. This survey contains every establishment with more than 10 employees and reports value-added, sales, employment, and several types of capital stocks and investment. Data starting in 1990 is available, but 2010 is excluded due to serious numbers of missing values for capital stocks.
Before calculating the gains from hypothetical liberalization from distortions, we trim the 1% tails of log(TFPRsi / TFPRs) and log(Asi / Asi) across industries. We then recalculate the variables used as components. In the periods analyzed, the standard industrial classification in Korea was revised three times (1991, 1998, and 2006); hence, the time-series discontinuities at the industry level may affect the results. Thus, we unify the industry classification for all periods at the three-digit level with the eighth industrial classification. A unit of this data is an establishment and not a firm in this survey. For convenience, we use firm and establishment interchangeably and only connote a difference between them when necessary.
Table 1 and Table 2 show that variances of TFPQ and TFPR for Korea, the U.S. and China. The data for the U.S. and China are quoted from Hsieh and Klenow (2009), but observations of Japan are not available. TFPQ indicates the physical productivity of a firm. This variable shows that the variance for Korea is greater than that of the U.S. and similar to that of China. However, the dispersion of TFPQ is not directly related to distortions in resource allocation, as technological differences between firms can be endogenous.
The variance of TFPR is closely related to misallocation. The standard deviation and the interquartile range of the Chinese data are largest in both cases, while those in the U.S. data are the smallest. From Tables 1 and 2, we know that the variance of the TFPR of China is larger than that of Korea despite the fact that the variance of the TFPQ of Korea is larger than that of China for 1998, indicating less distortion in the Korean manufacturing sector compared to that in China. The variance of the TFPR of China converges to a level similar to that of Korea; thus, distortion in the Chinese manufacturing sector appears to be relieved. Caution is needed when making a comparison of the results of each country because differences in sampling can affect the results.
Table 3 shows the standard deviations of τYsi and τKsi from the Korean data from 1990 to 2012 and from the Japanese data from 1981 to 2008. Korea has a smaller standard deviation of τYsi than Japan, but Korea’s variance of τKsi is two times higher than the Japanese case. Literally, Korea has greater distortion in the relative price of capital to labor than that in Japan.
The ultimate purpose of this paper is to calculate the ratio of realized output to efficient output, as in (10). Table 4 shows these results by country. Keeping in mind that a careful comparison is required due to the different periods and sampling methods, a descending order in terms of allocative efficiency is as follows: U.S., Japan, Korea and China. In the absence of output and capital distortion, there is no significant difference between Korea (0.648) and Japan (0.679). If output distortion is eliminated, the ratios of current to efficient output are 0.816 for Korea and 0.810 for Japan, also indicating that distortion in either output market or capital market does not contribute solely to the results.
We also investigated changes in allocative efficiency in the time-series data. Figure 1 indicates that Y / Yefficient, remaining at 0.68 until the mid-1990s, decreased sharply during the Asian Financial Crisis during the years 1997 and 1998. In the early 2000s, it recovered to 0.65 but declined toward 2008 (the year the financial crisis struck), after which it showed a minor increase in 2012.
FIGURE 1.
CHANGES IN THE ALLOCATIVE EFFICIENCY Y / Yefficient OF KOREA’S MANUFACTURING FIRMS
Note: 1) Korea’s 2010 Survey of Mining and Manufacturing is a complete enumeration survey. However, the capital items account has been removed due to omitted data to ensure continuity.
Source: Author’s calculation of the Survey of Mining and Manufacturing by Statistics Korea.
The downward trend of allocative efficiency is still valid in plants that survive for all of the years and remain in the sample. In the sample, the entry rates are between 12 and 27% and the exit rates range from 11% to 26%. In order to check if the time series of allocative efficiency (Y / Yefficient) was mainly driven by changes in the productivity distribution caused by entering and exiting plants, we construct a balanced panel. It was found that the time-series pattern of allocative efficiency does not change much compared to the original exercise. This finding implies that the fluctuation of misallocation is not greatly influenced by dropping unproductive plants and adding productive ones in Korea.
Table 5 summarizes the trend changes in Korea and Japan. By calculating the TFP gain (Yefficient / Y − 1), which indicates the potential advantage of eliminating misallocations, we find that the inefficiency of Japanese manufacturing firms increased through the 1980s to the 2000s. The gain from hypothetical liberalization in Japan is 43.7% in 1980, 47.9% in 1990 and 50.2% in 2000 (until 2008). In Korea, the TFP gain becomes 59.64% in the 2000s, and it stood at 48.32% in 1990, meaning that instances of misallocation has deepened at a rapid speed compared to that in Japan. When only the output market distortion is removed, the TFP increases by 18% in the 1990s and by 26% in the 2000s. Although both Korea and Japan undergo worsening degrees of capital distortion, the speed of the increase in inefficiency in the capital market is much faster in Korea.
This result may change depending on the data treatment for outliers. In this paper, we cut the top and bottom of 1%, following Hsieh and Klenow (2009). When the threshold increases by 2%, the level of inefficiency slightly falls off as variance of TFPRsi decreases. However the increasing trend of inefficiency remains apparent. Extreme values of the upper tail and lower tail do not control the empirical results.
The aggregation of industrial classification can affect the results. We calculate Y / Yefficient with the two-digit industrial classification. In this case, the variance of TFPRsi increases; thus, Y / Yefficient falls compared to the use of three-digit aggregation. However, the degree of intensified misallocation does not make a major change at all. Moreover, the pattern of the decreasing trend in efficiency remains valid even when the two-digit classification scheme is used. Therefore, aggregation of the industrial classification does not alter the results significantly.
Productivity studies show that the contribution of a firm’s entry and exit is quantitatively considerable. Although the method does not consider extensive margins, entries and exits occur frequently in the actual data. A balanced panel was established to observe the effects of entries and exits on Y / Yefficient . We constructed the balanced panel of data in two parts. The first consists of establishments surviving from 1990 to 1999, and the second contains firms which were operating from 2000 to 2012. If only firms who survive for the entire period (1990-2012) are selected, a limited number of firms remain, leading to survivorship bias. The results from the two parts of the balanced panel depict time-series trends which are quite similar to that in the original result. The effects of entries and exits appear to be limited for this measure of allocative efficiency.
Oberfield (2013) overcomes the limitations of the HK method by allowing that ① firms within an industry can have different degrees of capital elasticity to output, and ② factors can move between industries. Following Oberfield (2013), we can confirm that the technological differences between firms do not determine the main result of the decreasing trend of allocative efficiency. An important point from the results in Oberfield (2013) is that within-industry misallocation is the main contributor to inefficiency in the Korean case, in contrast to the Chilean manufacturing sector.
Figure 2 suggests that the overall allocative efficiency, Mboth, has trended downward from the 1990s onward. Mboth consists of MW and MB, which denote the extent of misallocation for intra-industry and inter-industry cases, respectively. As shown in the graph, intra-industry allocative efficiency drives Mboth down, while inter-industry misallocation does not show significant changes over time. Note that the level of MW, the counterpart of allocative efficiency in the HK method, is slightly higher than that in the HK method because MW allows individual capital elasticity, which was regarded as a form of distortion by Hsieh and Klenow (2009).
Table 6 presents TFP decomposition caused by the technological advances of a representative firm and the changes in misallocation. In the Korean manufacturing sector, the annual TFP (Solow residual) growth rate was approximately 5.6% on average during 1990-2009 and the allocative efficiency (d ln MW + d ln MB) worsened by nearly 0.6% on an annual basis. In other words, the TFP growth rate would have reached 6.2% if there had been no degeneration of allocative efficiency. “0.6%” is not a minor amount considering that increasing TFP growth by 1% cannot easily be done with artificial policies.
IV. Analysis of Changes in Allocative Efficiency
In order to analyze the factors behind the changes in allocative efficiency, this section investigates at the efficiency distributions of firms by size and age.
Y / Yefficient can be calculated at the level of each establishment. The current output of a firm is proportional to its productivity and distortion in (11). The percentage deviations of the current output PsiYsi from the efficient output Psi*Ysi* are expressed by (12). If τYsi is smaller and τKsi is larger than the industry mean, it is beneficial for the aggregate output for this plant to increase its production because Psi*Ysi* is greater than PsiYsi. If there is a negative correlation between τYsi and τKsi, Psi*Ysi* / PsiYsi would be amplified.
Table 7 shows how the size of the initially large vs. small plants would change if the TFPR were equalized in each country. The entries are the unweighted shares of plants. The rows are the initial (actual) plant size quartiles, and the columns are the bins of the efficient plant size relative to the actual size: 0%–50% (where the plant should shrink by half or more), 50%–100%, 100%–200%, and 200+% (where the plant should at least double in size). Although the aggregate output increases in the optimal case when distortions are removed, many establishments of all sizes would shrink. In the U.S., China, and India in Hsieh and Klenow (2009), initially large plants are less likely to shrink and are more likely to expand. The remarkable feature in Korea is that this pattern is much more pronounced. For the top size quartile in Korea, the share of plants which produce less than their efficient level is 16.3% (100%-200% + 200+%), while this rate is 10.6% in the U.S. and 12.0% in China. In contrast, the share of plants which should shrink in terms of efficient output is higher in Korea than in other countries. For the plants located in the bottom quartile, the share of plants which produce more than their optimal output is 19.1% (0%-50% + 50%-100%), while it is 16.7% in the U.S. and 16.4% in China.
Figure 3 shows the related average 100 log(Ysi / Yefficient,si) of each percentile with reference to the plant size. This shows that the larger the firm, the less the firm produces compared to its efficient level, with the degree of the tendency quantitatively intensifying. This figure reinforces the results shown in Table 7.
The results also imply that many small-sized establishments are uncompetitive in the Korean manufacturing sector. In other words, small-sized establishments exploit factor inputs which exceed the optimal amounts. Thus, it is favorable for the entire economy when unproductive small-sized establishments reduce their production and more productive, large plants take resources which had been held by these small establishments. Indirectly, it also implies that unselective support for all small-sized establishments may impede the healthy circulation of exits by unproductive plants and entries by productive ones.
Figure 4 displays the patterns of production compared to the efficient level in terms of the plant age. Generally, it was found that the younger the firms, the less they produced compared to the efficient production level and the older the firms, the more excessively they produced. The older the firm, the further the deviation of the actual output from the efficient level above zero, yet the extent of deviation does not exceed 10%.
Financial friction and adjustment costs are commonly mentioned as the main culprits behind instances of capital misallocation. Financial constraints are considered as an important difference between rich and poor countries, leading to productivity gaps by country (Banerjee and Duflo 2005). However, Midrigan and Xu (2009) point out that financial friction contributes little to account for the variance of the average product of capital using Korean manufacturing survey data identical to ours.2 Hsieh and Klenow (2009) examine how much differences in adjustment costs explain the extent of misallocation for the U.S., China, and India. The variations in the adjustment costs explain only a modest amount of the overall dispersion in the TFPR. Midrigan and Xu (2009) also mention the role of adjustment costs and conclude that the quantitative effect of adjustment costs on misallocation is marginal.
V. Concluding Remarks
Allocative efficiency in the Korean manufacturing sector (0.65) showed a downward trend from the 1990s to 2012. On average, allocative efficiency is approximately 0.65, which is lower than that of the U.S. (0.73), similar to the level in Japan (0.68) and higher than that in China (0.50). If allocative efficiency does not decrease in the case of Korea, the manufacturing TFP growth rate is estimated to climb by an additional 0.6%p on an annual basis.
As the productivity gap between large and small plants in Korea is higher than those in other countries, this paper empirically presents that the over-production of small-sized plants and the under-production of relatively large plants are noticeable. This implies that one type of distortion which makes the market less efficient may be extensive subsidies to small-sized plants. However, caution is needed when interpreting this empirical result regarding productivity differences by size. First, even within the same industry which is narrowly defined, products by small and large plants may not be homogeneous. In such a case, a unilateral comparison of productivity by size is not appropriate because goods markets are different. Second, there is a possibility that unfair vertical relationships enjoyed by large firms with small subcontractors may contain a measurement error of productivity. The productivity of large firms may be overestimated and that of small firms may be underestimated. As such, there may be deviations in estimations of efficient production rates. Third, we should be more careful when devising firm-related policy implications using the results, as our analysis is dependent on plant-level data and not firm-level data. Even bearing these possibilities in mind, the clear pattern of under- and over-production by size, as in Figure 3, stresses that this consistent pattern by size likely does not derive only due to heterogeneous products or from abuse by the market dominance of large firms.3 From this perspective, this paper recommends that it is desirable to concentrate more on selective support for younger and smaller firms with consideration of their growth potential rather than on providing unilateral support to all small-sized firms.
Notes
This figure represents the ratio of current output relative to the potential output in the absence of misallocation.
Midrigan and Xu (2014) note that the potential effect of financial frictions can be large because it impedes the entry of productive plants without enough money into the market.
Specifically, large firms’ partners in vertical relationships are usually medium-sized firms. However, nearly 77% of plants (establishments) in the manufacturing sector are in fact firms (a firm has one plant), and 87% of them are plants with fewer than 20 employees. This suggests that the left side of Figure 3 may not be related to large contractors.
References
, & (2009). Misallocation and Manufacturing TFP in China and India. Quarterly Journal of Economics, 124(4), 1403-1448, https://doi.org/10.1162/qjec.2009.124.4.1403.
, & . (2014, February). Finance and Misallocation: Evidence from Plant-level Data. American Economic Review, 104(2), 422-458, https://doi.org/10.1257/aer.104.2.422.
. (2013, January). Productivity and Misallocation during a Crisis: Evidence from the Chilean Crisis of 1982. Review of Economic Dynamics, 16(1), 100-119, https://doi.org/10.1016/j.red.2012.10.005.