
- P-ISSN 2586-2995
- E-ISSN 2586-4130


A person’s life consists of two important stages: the first stage as a student and the second stage as a worker. In an integrated model of education and career concerns, I analyze the welfare effects of education. In Spence’s job market signaling model, education as a sorting device improves efficiency by mitigating the lemon market problem. In contrast, in the integrated model, education as a sorting device can be detrimental to social welfare, as it eliminates work incentives generated by career concerns.
education, signaling, career concerns
D86, G38
Life consists of two important stages. In the first stage, as students, people decide how much education to obtain. In the second stage, as workers, they choose jobs and exert effort in the workplace (and then they retire). Therefore, education and careers are two important choices people make in life. However, people do not choose education and careers independently. They choose education while anticipating its impact on their future careers. However, the existing literature rarely considers possible interactions between education and careers. The standard model of (stand-alone) education is the job market signaling model of Spence (1973), in which education is used to signal workers’ hidden productivity to the labor market. The standard model of (stand-alone) careers is the career concerns model of Holmstrom (1999), in which workers exert efforts to achieve good performance, which signals to the labor market that they are talented workers. Although the education and career concerns literatures starting from the two aforementioned seminal papers are both vast, little work has been done on the interactions between education and career concerns.
This paper examines an integrated model of education and career concerns. By explicitly considering the interactions between education and career concerns, I find new welfare implications of education: if society uses education to sort agents according to productivity, then education could reduce the total surplus. This is inconsistent with Spence’s standard job market signaling model, which implies that education as a sorting device enhances welfare (even if it has no human capital value). Suppose that there are high type and low type agents. The labor market treats them equally, as they are indistinguishable. In such a case, high type agents leave and only low type agents prevail in the labor market (with an appropriate assumption on reservation payoffs). This loss of top talent (i.e., the lemon market problem) can be resolved if education reveals hidden types.
This story of the lemon market problem, however, may be overturned if not merely hidden productivity (type) but also hidden effort can contribute to output. Suppose that there exists a post-education work stage, in which an agent exerts effort to produce output. If the labor market does not fully know the agent’s hidden productivity, she works diligently to demonstrate her talent. However, if education reveals the hidden talent, she is demotivated, exerts little effort, and hence output decreases. Therefore, education as a sorting device could be detrimental to welfare.
This paper is organized as follows. Section II presents an integrated model of education and career concerns. Section III analyzes the welfare implications of education. Section IV discusses an important technical issue in the integrated model. Spence’s standard model has a unique separating equilibrium and no pooling equilibrium if one uses the Intuitive Criterion suggested by Cho and Kreps (1987), a standard equilibrium refinement. If the integrated model also has no pooling equilibrium, this paper’s main welfare implication has of little value. In Section IV, I argue that pooling equilibria could survive the Intuitive Criterion in the integrated model. Section 5 presents the conclusion.
An agent’s hidden productivity θ is either h (high) or l (low) where 0 = l < h < 1. There are many agents whose total measure is normalized to one. One half is of high type and the other half is of low type.
The timeline is as follows. There are three periods t = 0, 1, 2. At t = 0, each agent as a student chooses a publicly-observable education level e∈[0, ∞) at the cost of education C(θ , e) such that C(θ , 0) = 0, Ce > 0, Cθ < 0, and Ceθ < 0 , where the lower subscript denotes the (cross-) partial derivatives. At t = 1, 2, the competitive labor market pays wage wt ; Given wt , each agent as a worker chooses privately-observable effort level at ∈[0, a] at the cost of effort c(at) such that c(0) = c' (0) = 0, c' > 0, and c'' > 0; Given at , a publicly-observable output yt ∈ { 0, 1} is realized.
Effort and productivity contribute to output in the following manner: let f( θ, at) be the conditional probability of success
Note that the probability of success increases with effort and productivity. (The following analysis holds even if f(θ , at) has a general functional form such that fa > 0 and fθ > 0 ). To ensure that f( θ , at) ≤ 1 for any at ∈ [0, a], it is necessary to assume that a ≤ 1 − h. Given that yt ∈ {0, 1} , one can interpret f(θ , at) as the expected output conditional on (θ , at).
I assume that the labor market is competitive, and hence wage wt equals the market’s expectation of output. I assume that output yt is not contractible.
Given a wage structure, a type θ agent’s preference is represented by
where δ ∈ (0, 1) is the discount factor and 𝔼θ [·|·] denotes the type θ agent’s expectation with respect to the relevant information structure.
Below, I consider two cases. First, high type agents choose a higher level of education than low type agents—separating equilibrium. Second, both types choose the same level of education—pooling equilibrium.
Note that education has no human capital value. It can only signal hidden productivity. Thus, the most reasonable case is one in which low type agents choose zero education while high type agents choose the minimum level of education, which the low type agents cannot mimic because of higher cost of education. This separating equilibrium is known as the Riley equilibrium. I confine my attention to the Riley equilibrium, which is later shown to be the only separating equilibrium that satisfies the Intuitive Criterion suggested by Cho and Kreps (1987).
In the Riley equilibrium, types are revealed, as is the expected output. Suppose the
market expects that 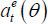 will be chosen in equilibrium. A type θ agent’s wage is then, for t = 1, 2,
will be chosen in equilibrium. A type θ agent’s wage is then, for t = 1, 2,
That is, the wage is fixed and independent of effort at (though it depends on 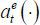 ). Let
). Let 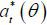 denote the equilibrium effort type θ agent actually chooses. Because effort is costly and has no effect on wages, it follows
that
denote the equilibrium effort type θ agent actually chooses. Because effort is costly and has no effect on wages, it follows
that 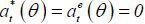 in rational expectations equilibria.
in rational expectations equilibria.
Let e(θ) be the equilibrium level of education, which the type θ agent chooses. Thus, e(l) = 0 and e(h) > 0. Note that e(h) represents the minimum education level low type agents cannot profitably mimic. That is, e(h) is characterized by
Let uθ denote the type θ agent’s reservation payoff, which she can obtain by leaving the labor market. This is perhaps the payoff of self-production or of participating in an alternative labor market. I assume that ul = 0 for simplicity and that
Assumption 1 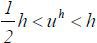
Assumption 1 implies that the lemon market problem exists: high type agents will not participate unless the types are revealed, despite the fact that their participation is socially efficient. I also assume that education is not prohibitively costly for the high type (though it is highly costly for the low type):
Assumption 2 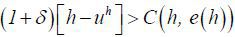
(3) implies that Assumption 2 holds if the education cost decreases sufficiently with productivity. Assumption 2 implies that the high type willingly participates in the labor market by undertaking costly education, as the hidden type is reveled, and therefore, a higher wage is promised.
The total surplus in this Riley separating equilibrium is given by
as the low type agent’s utility equals zero regardless of whether or not they participate.
As for a benchmark case, suppose that education cannot be used as a sorting device. Due to the lemon market problem, the total surplus is then given by
Assumption 2 and equations (4) and (5) imply that education as a sorting device mitigates the lemon market problem by inducing high type agents’ participation in the labor market. Furthermore, education as a sorting device improves efficiency in the Paretian sense, as low type agents’ payoffs are unchanged while high type agents’ payoffs increase.
In a pooling equilibrium, education has no sorting effect, and hence, the labor market cannot distinguish types. Given that education has no role but is only costly, I confine my attention to the most efficient pooling equilibrium, in which both type agents choose zero education. In Spence’s standard job market signaling model, where interactions between education and career concerns are ignored, this pooling equilibrium fails to satisfy the Intuitive Criterion. Later, I shall discuss that this is not the case if one considers the interactions between education and career concerns.
Suppose that the market expects that 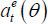 is chosen in equilibrium. Let
is chosen in equilibrium. Let 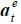 denote
denote 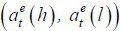 and 𝔼m denote the market’s expectation conditional on
and 𝔼m denote the market’s expectation conditional on 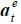 . Then, wages are given by
. Then, wages are given by
Importantly, the date-2 wage (i.e., the expected date-2 output) depends on the date-1 output y1 . This is because market observes the date-1 performance y1, which is informative of an agent’s hidden productivity θ , which determines the date-2 performance y2 . (In a separating equilibrium, in contrast, the date-1 performance has no value of information, as the hidden productivity is already unraveled). This observation is crucial in this paper. Even if there are no explicit incentive contracts, agents face date-1 incentives because the date-1 effort (stochastically) determines the date-1 output, which determines the date-2 wage. However, the date-1 wage is fixed and independent of output, as no output is realized in the beginning of date-1.
To observe this formally, note that at date-2, a type θ agent maximizes w2 (y1) − c(a2). Since w2 (y1) is independent of a2 (while it depends on 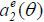 ), the agent chooses
), the agent chooses 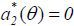 for θ = h, l. Then, in rational expectations equilibria, it follows that
for θ = h, l. Then, in rational expectations equilibria, it follows that 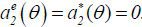 . At date-1, the agent chooses
. At date-1, the agent chooses 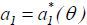 , which maximizes
, which maximizes
where 𝔼θ is the type θ agent’s expectation conditional on θ and 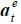 . Since a1 affects the probability of
. Since a1 affects the probability of 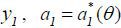 , is characterized by the following first-order condition
, is characterized by the following first-order condition
In general, 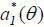 depends on θ , as fa( θ, a1) depends on θ . Given the simplification that f(θ, at) = θ + kat, however,
depends on θ , as fa( θ, a1) depends on θ . Given the simplification that f(θ, at) = θ + kat, however, 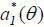 is independent of θ , though the main result of this paper is robust to the functional form of f(θ, at) under certain regularity conditions.1 Thus, I let
is independent of θ , though the main result of this paper is robust to the functional form of f(θ, at) under certain regularity conditions.1 Thus, I let 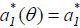 and
and 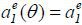 . One may expect that the wage wedge [w2(1) − w2(0) ] is positive. This is true because better date-1 performance implies that hidden
productivity is greater, indicating that the expected date-2 performance would be
greater. The following lemma provides a formal account.
. One may expect that the wage wedge [w2(1) − w2(0) ] is positive. This is true because better date-1 performance implies that hidden
productivity is greater, indicating that the expected date-2 performance would be
greater. The following lemma provides a formal account.
Lemma 1 The marginal incentive in (9) is positive, independent of θ , and equal to
where VARm is the market’s assessed variance conditional on 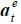 .
.
Proof: First of all, the marginal incentive is positive since the variances are always nonnegative and θ is a nondegenerate random variable from the market’s perspective. Independence with respect to θ is obvious. Next, I shall prove that [w2(1) − w2(0)] equals the ratio of variances. Initially, the wage is given by
where ℙm(h|y1) is the market’s posterior of θ = h given y1 and 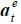 . This posterior is given by
. This posterior is given by
Then, it follows
Note that the numerator equals 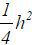 , which equals VARm (θ ) since
, which equals VARm (θ ) since
The denominator equals VARm (y1) since
where 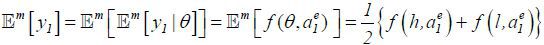 . ■
. ■
Lemma 1 implies that the date-1 marginal incentive is determined by the signal-to-noise ratio—the extent to which the data y1 conveys information about a hidden variable θ . Holmstrom (1999) finds the same result under a simpler model in which neither the market nor the agent knows the hidden type. Thus, making θ private information does not affect the size of the career concerns motive of work incentives under the current specification, in which the expected output is linear in θ and at (i.e. f(θ, at ) = θ + kat ). In a more general specification, work incentives depend on θ .
A key observation from (10) is as follows. If an agent’s hidden ability is not revealed to the labor market, the agent faces date-1 work incentives in order to convince the market that she is of high ability.
The next lemma demonstrates the existence of a rational expectations equilibrium 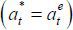 . Note that w2 (y1) depends on
. Note that w2 (y1) depends on 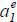 . To highlight this dependence, I write
. To highlight this dependence, I write 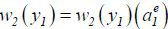 .
.
Lemma 2 Suppose 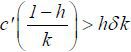 . Then, there exists a rational expectations equilibrium
. Then, there exists a rational expectations equilibrium 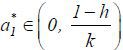 such that
such that
Proof: Let 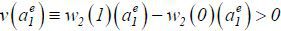 . In addition, let
. In addition, let 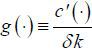 . Then, (*) there exists a unique
. Then, (*) there exists a unique 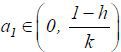 for each given
for each given 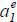 such that
such that 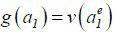 since c' (0) = 0,
since c' (0) = 0, 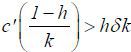 , and
, and 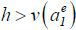 . Then,
. Then, 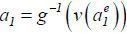 . Let
. Let 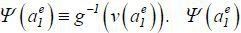 is a continuous function on the closed interval
is a continuous function on the closed interval 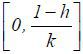 to the same interval. Then, the Brouwer fixed point theorem and (*) imply that there
exists an
to the same interval. Then, the Brouwer fixed point theorem and (*) imply that there
exists an 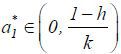 such that
such that 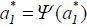 . That is, there exists a rational expectations equilibrium
. That is, there exists a rational expectations equilibrium 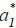 . ■
. ■
Given the equilibrium effort 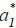 , the date-1 wage equals
, the date-1 wage equals
Additionally, according to (11), a type θ agent’s expectation of the date-2 wage equals
Subsequently, a type θ agent’s payoff equals
Note that this payoff increases with the level of equilibrium effort 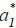 since (9) implies that
since (9) implies that 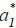 is lower than the first-best effort, which maximizes ka − c(a) . Thus, if there are two equilibrium efforts, a' and a'' such that a' < a'', then every agent is strictly better off with a'' than a' . Therefore, the remaining part of this paper focuses on the maximum (or the supremum)
of equilibrium efforts based on the notion of the Pareto optimality.
is lower than the first-best effort, which maximizes ka − c(a) . Thus, if there are two equilibrium efforts, a' and a'' such that a' < a'', then every agent is strictly better off with a'' than a' . Therefore, the remaining part of this paper focuses on the maximum (or the supremum)
of equilibrium efforts based on the notion of the Pareto optimality.
Note that low type agents will always participate in the labor market, as their reservation payoff ul is zero. However, high type agents will participate if and only if
Assumption 3 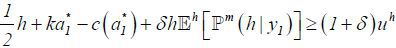
To observe when high type agents profitably participate, suppose for the moment k = 0, and hence, 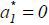 by (10). Note that 𝔼θ [ ℙm(h| y1)]∈(0,1) is the type θ agent’s expectation of the market’s posterior given y1 . High type agents are more optimistic about the future than low type agents, as
they know their superior ability:
by (10). Note that 𝔼θ [ ℙm(h| y1)]∈(0,1) is the type θ agent’s expectation of the market’s posterior given y1 . High type agents are more optimistic about the future than low type agents, as
they know their superior ability: 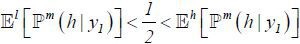 . This is related to the market’s learning effect. The labor market updates its expectation
of date-2 output by observing the date-1 output. High type agents then expect more
income, as the date-1 output is (stochastically) higher. If the learning effect is
slight (i.e.,
. This is related to the market’s learning effect. The labor market updates its expectation
of date-2 output by observing the date-1 output. High type agents then expect more
income, as the date-1 output is (stochastically) higher. If the learning effect is
slight (i.e., 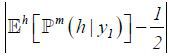 has a small value), Assumption 1 implies that Assumption 3 is violated. If instead
the learning effect is large enough, Assumption 3 is satisfied.
has a small value), Assumption 1 implies that Assumption 3 is violated. If instead
the learning effect is large enough, Assumption 3 is satisfied.
Even if the learning effect is slight, if k > 0 and the surplus 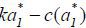 generated by career concerns is large enough, then Assumption 3 is satisfied.
generated by career concerns is large enough, then Assumption 3 is satisfied.
As long as high type agents find it optimal to participate (i.e. Assumption 3 holds),
the total surplus in this pooling equilibrium is 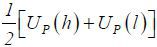 , which equals
, which equals
according to the martingale property, that is, the expectation of the posterior equals its prior.
By comparing (14) to (4), it is apparent that the total surplus in the pooling equilibrium
is greater than that in the Riley separating equilibrium. That is, the use of education
as a sorting device reduces the total surplus. There are two reasons. First, education
as a signaling device reveals hidden productivity. Thus, agents need not persuade
their ability to potential employers in the labor market, which means that their post-education
work incentives (motivated by career concerns) are eliminated. In consequence, the
work stage surplus 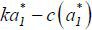 is not realized. Second, education is wasteful and incurs cost C(h, e(h)) .
is not realized. Second, education is wasteful and incurs cost C(h, e(h)) .
The detrimental effect of education as a sorting device hinges on Assumption 3. If this assumption is not satisfied, only low type agents participate in the labor market. Expecting this fact rationally, the market then pays zero to the participants. Thus, the total surplus in the pooling equilibrium equals
Thus, we return to the standard result, where the use of education as a signaling device improves the total surplus. One might wonder when Assumption 3 is more likely to be satisfied. This depends on h and uh . The degree of the lemon market problem can be measured by | h − uh | since adverse selection discourages the participation of high type agents in the labor market. Note that Assumption 3 holds if h is large or uh is small, as in this case high type agents will participate even if the work stage surplus is relatively low. Thus, Assumption 3 is satisfied if the degree of the lemon market problem is severe, which is of high interest, whereas it is violated if the lemon market problem is not very important, which is of little interest. In the standard Spence model in which the post-education work stage is ignored, education as a sorting device is more beneficial if the lemon market problem is more severe. However, in this very case, education as a sorting device is more detrimental if the post-education work stage is explicitly considered.
Summarizing the analysis brings the following main result:
Proposition 1 Suppose that the lemon market problem exists (i.e., Assumption 1) and that education is not prohibitively costly (i.e., Assumption 2). Then,
(i) If there is no post-education work stage, the use of education as a sorting device increases the total surplus.
Suppose for the following that there is a post-education work stage.
(ii) If high type agents profitably participate in the labor market in the most efficient pooling equilibrium (i.e. Assumption 3), which is the case when the lemon market problem is severe, then education as a sorting device decreases the total surplus.
(iii) If high type agents cannot profitably participate in the most efficient pooling equilibrium (i.e. Assumption 3 is violated), which is the case when the lemon market problem is unimportant, then education as a sorting device increases the total surplus.
In the following, I consider three extensions. In the first extension, I consider multiple types. Productivity is determined by various hidden factors. For instance, intelligence and fitness-to-work are two important factors that contribute to overall productivity. Let θ1 denote intelligence, which agents observe but the market does not. The marginal cost of education Ce(θ1, e) decreases in θ1 . Let θ2 denote fitness-to-work, which is unobservable to agents and the market. Let θ ≡ g(θ1 ,θ2) be productivity, where g increases in each argument. In this case, education can reveal only θ1. Lemma 1 then implies that an agent’s post-education marginal incentive under separating equilibria equals
while the marginal incentive under pooling equilibria equals
That is, the marginal incentive is greater under pooling equilibria. This result holds irrespective of whether or not θ1 and θ2 are independent. That is, the more information education reveals, the more likely it will be detrimental to welfare.
In the second extension, I assume that education has both a human capital-enhancing effect and a sorting effect. This situation can be modeled in the following way: the overall productivity θ' equals θ + αe, where α > 0. In this case, the welfare implication of education is ambiguous. On the one hand, it improves efficiency by raising productivity. On the other hand, it reduces efficiency by discouraging post-education work incentives.
In the third extension, explicit incentive contracts are considered. Thus far, I have assumed that workers face only the implicit incentive generated by career concerns but not an explicit incentive provided by a performance-based contract. Suppose instead that output yt is contractible at no cost. Then, the linear contract wt (yt) = yt − K, where K is a constant, induces the first-best effort since the agent becomes a residual claimant. However, such a ‘perfect’ contractibility is not satisfied in many real-life principal-agent relationships. Performance measures of workers in administration offices are often nonverifiable. Subjective and hence non-contractible performance measures (such as quality) often contain more information than objective performance measures (such as quantity). For these reasons, suppose that yt is non-contractible. Let pt be a contractible but imperfect performance measure. Workers then face an imperfect explicit incentive generated by a contract wt(pt). The implicit incentive generated by career concerns could then complement the imperfect explicit incentive. Therefore, education as a sorting device could reduce the welfare to an extent, which increases in the imperfectness of pt.
Proposition 1 implies that uncertainty in types is beneficial for social welfare. This seems at odd at a first glance, as one might expect that the uncertainty, as a source of market failure, reduces social welfare. However, this is consistent with the general theory of second-best suggested by Lipsey and Lancaster (1956): if there is an existing source of market failure (so that the economy is in a second-best outcome), an additional source of market failure could either increase or decrease social welfare (see Milgrom and Roberts (1982) and Kim (2004) for other examples of the general theory.) However, Proposition 1 is not a simple corollary of the general theory. In fact, the general theory is too general to explain why an additional source of market failure is socially beneficial; the general theory only raises the possibility that an additional market failure is beneficial.
Proposition 1 is also related to the information disclosure literature. In a dynamic tournament setting, Ederer (2010) shows that disclosing interim performance can reduce incentives due to the trade-off between evaluation and motivation effects. In the presence of career concerns and relational contracting, Mukherjee (2008) shows that if the current employer discloses workers’ performance levels to the labor market, the career concerns motive of incentives increases, whereas the effectiveness of relational contracting is reduced. Proposition 1 is, however, different from these papers in that (1) it examines the effect of disclosing types rather than performance on incentives and (2) these papers consider only post-education workplace behaviors, while the present study considers both education and post-education behaviors.
There are infinitely many separating and pooling equilibria in the standard job market signaling model (where there is no post-education work stage). However, Cho and Kreps (1987) show that only the Riley separating equilibrium (and no pooling equilibria) satisfies their Intuitive Criterion, which currently is the standard equilibrium refinement criterion, and is hence reasonable. Recently, Alos-Ferrer and Prat (2012) show that certain pooling equilibria can satisfy the Intuitive Criterion if there is learning by the market (or employers). If there is a post-education work stage, as in this paper, pooling equilibria are more likely consistent with the Intuitive Criterion. These points are elaborated below.
Consider initially the standard job market signaling model. Let (el, eh) be a non-Riley separating equilibrium such that el = 0 and eh > e(h), where e(h) is given by (3). (Note that el cannot be positive since otherwise low type agents profitably deviate to zero education). Then, if an agent chooses e' such that, e(h) < e' < eh , the market should not believe that the agent is high type since otherwise high type agents profitably deviate to e' . However, such a belief is not intuitive for the following reason. If low type agents deviate to e', they are worse off even in the best scenario in which the market believes them as high type and hence pays h rather than l . If high type agents deviate to e', they are better off in the best scenario. That is, low type agents never deviate while high type agents may deviate. Thus, the market should believe that those who deviate to e' are high type. Therefore, if only the intuitive belief is allowed, as required by the Intuitive Criterion, (el , eh) is no longer a separating equilibrium. Nothing changes in this argument even if one introduces a post-education work stage, as there is no uncertainty in types.
Consider the standard job market signaling model. Let eP be a pooling equilibrium. Then, there is 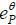 such that
such that
It follows then 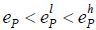 . Suppose that eP is a pooling equilibrium. Then, the market should not believe that the agent who
deviates to
. Suppose that eP is a pooling equilibrium. Then, the market should not believe that the agent who
deviates to 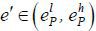 is high type, since otherwise high type agents profitably deviate to e' . But this belief is not intuitive. By deviating to e', low type agents are worse off even under the best scenario (i.e., the market believes
them as high type), while high type agents are better off under the best scenario.
Thus, only high type agents may deviate to e', and hence, the market should believe that those who choose e' are high type. If only this type of intuitive belief is allowed, eP is no longer a pooling equilibrium.
is high type, since otherwise high type agents profitably deviate to e' . But this belief is not intuitive. By deviating to e', low type agents are worse off even under the best scenario (i.e., the market believes
them as high type), while high type agents are better off under the best scenario.
Thus, only high type agents may deviate to e', and hence, the market should believe that those who choose e' are high type. If only this type of intuitive belief is allowed, eP is no longer a pooling equilibrium.
However, this is not the case if one adds post-education learning by the market (or
employers). After the education choice, the output signal yt is realized. (To focus on the learning effect, I assume for now that k = 0 so that agents do not exert any work effort). By observing , y1 the labor market learns (partially) about the hidden type and then adjusts its expectation
of the date-2 output 𝔼m[θ | y1]. High type agents know that their date-1 output will be (stochastically) greater
than that of low type agents. Thus, even if types are not revealed in pooling equilibria,
high type agents expect larger incomes (i.e., 𝔼h[𝔼m[θ | y1]] > 𝔼l[𝔼m[θ | y1]]) Then, a high type agent’s gain from separating himself (by gaining more education
than eP ) from low type agents is lower than it is when there is no post-education learning.
To see this, note that 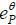 is determined via
is determined via
If this learning effect (𝔼h[𝔼m[θ | y1]] − 𝔼1[𝔼m[θ | y1]]) is large enough, it follows that 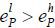 . Then, there is no education level e' such that low type agents are worse off even under the best scenario while high type
agents are better off under the best scenario. Thus, this pooling equilibrium satisfies
the Intuitive Criterion. (See Alos-Ferrer and Prat (2012) for more details).
. Then, there is no education level e' such that low type agents are worse off even under the best scenario while high type
agents are better off under the best scenario. Thus, this pooling equilibrium satisfies
the Intuitive Criterion. (See Alos-Ferrer and Prat (2012) for more details).
If one also considers post-education working (i.e., k > 0 ), then the pooling equilibria become more robust with respect to the Intuitive Criterion.
By separating himself from low type agents, high type agents lose the work stage surplus
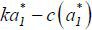 , which is realized only in pooling equilibria. If this surplus is large enough, high
type agents are worse off by separating himself from low type agents (by taking more
education than eP ) even in the best scenario. That is, for any e > eP, it follows that
, which is realized only in pooling equilibria. If this surplus is large enough, high
type agents are worse off by separating himself from low type agents (by taking more
education than eP ) even in the best scenario. That is, for any e > eP, it follows that
The pooling equilibrium eP then satisfies the Intuitive Criterion.
I revisit Spence’s signaling theory of education by providing an integrated model of education and career concerns. Under the absence of post-education career concerns, education as a sorting device improves welfare by mitigating the lemon market problem. Under the presence of post-education career concerns, sorting by education could be detrimental to social welfare, as it eliminates work incentives generated by career concerns.
Although this paper examines the welfare effects of education, one should be careful in drawing educational policy implications directly from the current paper, as the main result is based on several assumptions. Rather, the merit of this paper is that it provides a theoretic framework with which researchers may conduct thought experiments regarding possible dynamics of education, careers, incentives, and policies.
Assume a set of regularity conditions: fa > 0, fθ > 0 and faθ ≥ 0 for any (θ , a), where the subscripts denote (cross) partial derivatives. In this case, it can be
shown that  Although the equilibrium effort depends on type, it is unobservable by the market.
Thus, under the absence of education as a sorting device, the market cannot identify
the high type from the low type, and hence, the agent has work incentives. I thank
an anonymous referee for having pointed out to me the necessity of certain regularity
conditions.
Although the equilibrium effort depends on type, it is unobservable by the market.
Thus, under the absence of education as a sorting device, the market cannot identify
the high type from the low type, and hence, the agent has work incentives. I thank
an anonymous referee for having pointed out to me the necessity of certain regularity
conditions.
, & . (2012). Job Market Signaling and Employer Learning. Journal of Economic Theory, 147, 1787-1817, https://doi.org/10.1016/j.jet.2012.01.018.
. (2010). Feedback and Motivation in Dynamic Tournaments. Journal of Economics and Management Strategy, 19, 733-769, https://doi.org/10.1111/j.1530-9134.2010.00268.x.
. (1999). Managerial Incentive Problems: A Dynamic Perspective. Review of Economic Studies, 66, 169-182, https://doi.org/10.1111/1467-937X.00083.
, & . (1956). The General Theory of Second Best. Review of Economic Studies, 24, 11-32, https://doi.org/10.2307/2296233.
, & . (1982). Limit Pricing and Entry under Incomplete Information: An Equilibrium Analysis. Econometrica, 50, 443-459, https://doi.org/10.2307/1912637.
. (2008). Sustaining Implicit Contracts when Agents Have Career Concerns: the Role of Information Disclosure. RAND Journal of Economics, 39, 469-490, https://doi.org/10.1111/j.0741-6261.2008.00023.x.
. (1973). Job Market Signaling. Quarterly Journal of Economics, 87, 355-374, https://doi.org/10.2307/1882010.