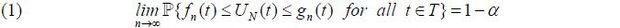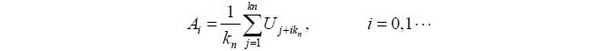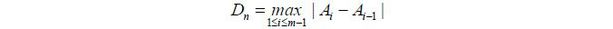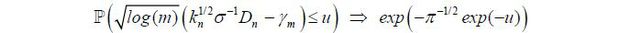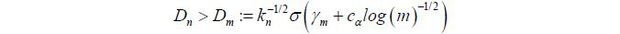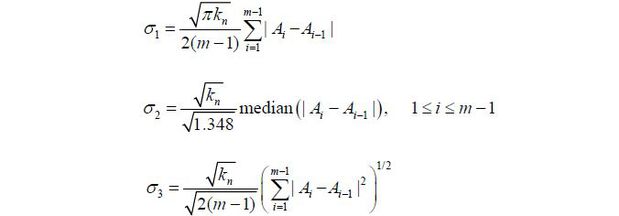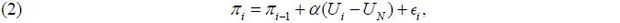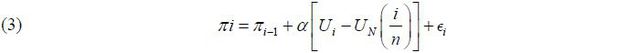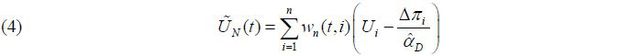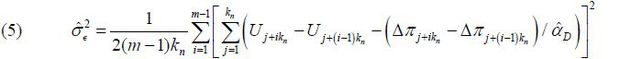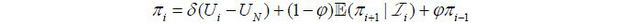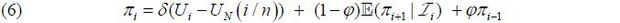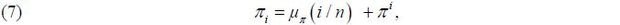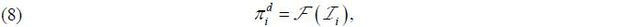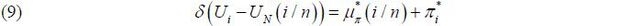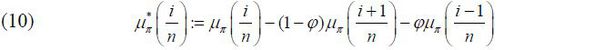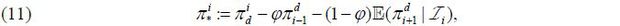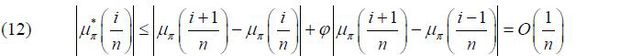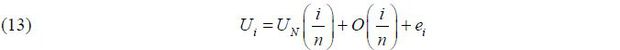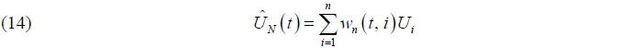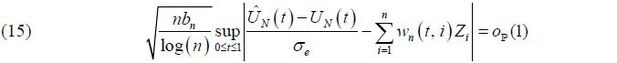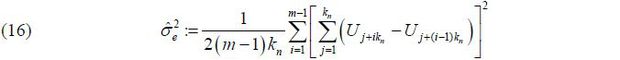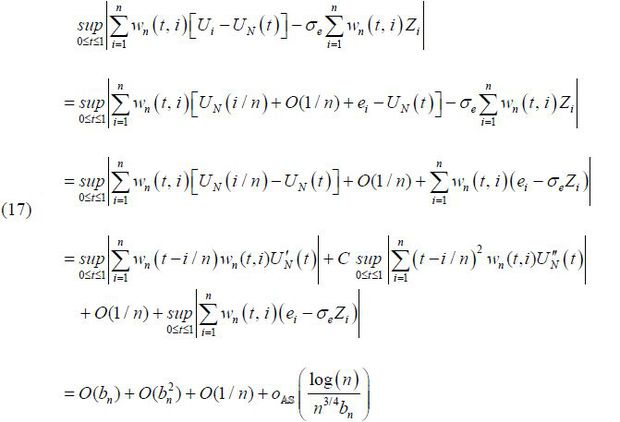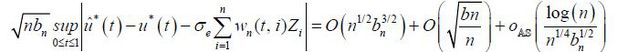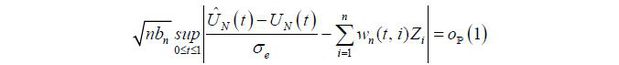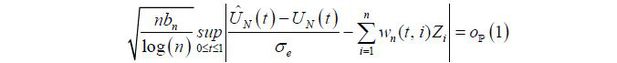Inference and Forecasting Based on the Phillips Curve†
Abstract
In this paper, we conduct uniform inference of two widely used versions of the Phillips curve, specifically the random-walk Phillips curve and the New-Keynesian Phillips curve (NKPC). For both specifications, we propose a potentially time-varying natural unemployment (NAIRU) to address the uncertainty surrounding the inflation-unemployment trade-off. The inference is conducted through the construction of what is known as the uniform confidence band (UCB). The proposed methodology is then applied to point-ahead inflation forecasting for the Korean economy. This paper finds that the forecasts can benefit from conducting UCB-based inference and that the inference results have important policy implications.
Keywords
Time-varying NAIRU, Random-walk Phillips curve, New-Keynesian Phillips curve, Uniform confidence band, Model validation, Inflation forecasting
JEL Code
C12, C13, C14
I. Introduction
Since Milton Friedman introduced the idea of the non-accelerating inflation rate of unemployment (NAIRU) in his presidential address to the American Economic Association in 1968, the NAIRU has served as a general guideline for those establishing macroeconomic policies. The idea has also been very useful as an empirical basis for predicting changes in the inflation rate. Among the various hypotheses regarding this important structural parameter, there has been a general recognition among many economists that if a NAIRU does exist, it must change over time (Stiglitz 1997; Ball and Mankiw 2002).
Perhaps the most widely accepted belief with regard to time-variation in the U.S. NAIRU is that the parameter has been falling since the early 1980s (Stiglitz 1997; Shimer 1998). Although this consensus on a decreasing NAIRU appears reasonable and is supported by empirical research in this area, there remains no formal justification of this hypothesis in the literature. Furthermore, there is a lack of evidence of any time-varying NAIRU for economies other than that of the U.S. Given this limitation, the paper conducts inference of the NAIRU parameter for the Korean economy and shows how the developed methodology can be applied to forecasting Korean monthly inflation.
To meet these goals, the paper considers two versions of the Phillips curve: the random-walk Phillips curve1 (Staiger, Stock, and Watson 1996, 1997) and the New-Keynesian Phillips curve (NKPC) (Gal´ı and Gertler 1999). Given the uncertainty surrounding the NAIRU, we extend the Phillips curves such that the new model framework can deal with uncertainty. That is, the NAIRU in the suggested framework does not assume any specific parametric form. Only data determine the unknown form, of which the estimate will be used to fore-cast inflation.
The unique feature of the approach in this work is that the proposed model validation procedures can be used directly for the forecasting exercise. Thus far, most studies of the Phillips curve in macroeconomics have focused on either model validation or on the forecasting performance, but not both. In this work, we generalize the two widely used versions of Phillips curve such that the modified models can incorporate the uncertainty surrounding the NAIRU parameter more efficiently. Uniform inference procedures for the model are proposed and used to suggest a new forecasting methodology that is applied to Phillips-curve-based inflation forecasting. Given that it attempts to combine these two rather distinct areas of research, the current work stands out among the numerous papers related to the forecasting ability of the Phillips curve.
Until recently, the empirical literature on the Phillips curve rarely provided inference based on estimates of the NAIRU parameter. A handful of pioneering works in this direction include those by Gordon (1997, 1998) and Staiger, Stock and Watson (1996, 1997, 2001), where the authors estimate a time-varying NAIRU in the traditional expectations-augmented Phillips curve (Friedman, 1968; Phelps, 1970) with adaptive expectations and construct its confidence intervals. Unfortunately, these works on the inference of the time-varying NAIRU involve only the construction of point-wise confidence intervals of the parameter. In the treatment of dynamic models, such as the NKPC with a time-varying NAIRU, it is more appropriate and more useful to construct uniform confidence bands (UCB) than their point-wise counterparts, as UCBs allow us to perform statistical inference for the parameter. That is, the UCB allows us to test whether the parameter assumes any specific structure (i.e., constant, linear) on it. In principle, point-wise confidence intervals/bands are not appropriate for testing these hypotheses on the parameter because any inference results based on point-wise outcomes pertain to one specific point only.
In order to construct the asymptotic UCB of the time-varying NAIRU UN(t) with the level 100(1-α )%, α ∈(0, 1) form, it is necessary to find the following two functions fn(·) and gn(·) based on the data:
where T = [0, 1]. The purpose of constructing the UCB above is to test whether the NAIRU UN(·) takes a certain parametric form. That is, using the UCB of UN(·) , we are able to test the null hypothesis H0 : UN(·) = Uθ(·) , where θ ∈ Θ and where Θ is a parameter space. For example, in order to test H0 : Uθ(t) = θ0 +θ1t, it is possibly simply to check whether 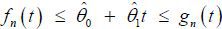 holds for all t∈T. Here
holds for all t∈T. Here 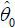 and
and 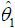 are the least squares estimates of θ0 and θ1, respectively. If it does hold for all t∈T, then we fail to reject the null hypothesis at level α.
are the least squares estimates of θ0 and θ1, respectively. If it does hold for all t∈T, then we fail to reject the null hypothesis at level α.
In general, the UCB is a more conservative confidence band than the traditional point-wise confidence band in the sense that the UCB is usually wider than its point-wise counterpart. Thus, test results based on the UCB would be more robust than those under the point-wise outcomes. For these reasons, the UCB has recently attracted more attention in the econometrics and statistics literature. For example, Baillie and Kim (2015) revisit the forward premium regression approach (Fama 1984) in an effort to understand the potential source of model instability. They undertake the UCB-based inference of the model parameters to identify the driving force behind the dynamics and to capture potential incidences of co-movement among the parameters for different currencies. Kim (2016) constructs a UCB of the non-parametric trend in a semi-parametric regression model, where the independent variables are non-stationary processes. The UCB is then used to test for a parametric specification of the unknown trend in the model. Given these interesting results, we shall construct the UCB of a time-varying NAIRU and carry out inference about the parameter.
The developed inference procedures can be applied to forecasting inflation variables. Given the UCB of NAIRU, one can test whether or not a certain parametric form is accepted. If it is accepted, then the estimated structure is used to forecast inflation, involving mainly the extrapolation of the data. If it is rejected, the non-parametric fits of the NAIRU can then be used to forecast the variable. Given that non-parametric fits vary over time, we need to combine these time-specific estimates for forecasting. We combine them by averaging the estimates. To compare the performances of the proposed method and of the traditional Phillips curve, the paper conducts a pseudo out-of-sample forecasting experiment. Both the entire sample and sub-samples are utilized to in an assessment of their performances in this experiment. The results and the implications are discussed in detail.
The organization of the paper is as follows: Section II discusses the methodology. The first part is for testing for any potential structural break in the data. We employ a non-parametric break test to rule out any potential bias from specifying a parametric form. The subsequent parts concern the inference that is carried out based on two popular versions of the Phillips curve - the random-walk Phillips curve (Staiger, Stock, and Watson 1996) and the new Keynesian Phillips curve (Gal´ı and Gertler 1999). The steps used to perform the inference are explained in detail. The section also discusses how forecasting is conducted based on the inference procedures. Essentially, the uniform confidence band is used to select an appropriate model that is eventually used for extrapolation. Section III explains the data used and summarizes and interprets the estimation and forecasting outcomes. This section also discusses the policy implications of the empirical results. Section IV concludes the paper and discusses potential future research. The proof of the theoretic result and the figures and tables are given in the appendix of the paper.
II. Methodology
Inference of the Phillips curve is carried out by the construction of a uniform confidence band (UCB) (Kim 2015, 2016; Baillie and Kim 2015). The UCB is a powerful tool for undertaking the inference of an unknown function in an economic causal model. Unlike the traditional point-wise confidence intervals, the UCB can be used for model validation by determining the correct function form. Because this is mostly done by a simple visual check of the result, the entire procedure is also very tractable. As discussed in the introduction, the stability of the NAIRU parameter in the Phillips curve is a major source of debate. The UCB-based inference method introduced here can be readily used for the validation of the Phillips curve and can potentially contribute to improving the accuracy of inflation forecasts based on the model.
A. Stability of the NAIRU Parameter
One of the issues to consider when applying the Phillips curve to the Korean economy in recent years is the potential parameter instability during the 1997 Asian financial crisis. The possible existence of what is known as a structural break due to this shock can basically invalidate the outcomes of any traditional analysis. Hence, it is desirable to determine this possibility before conducting the UCB-based inference of the Phillips curve for the Korean economy. Among the many available tests of change points, we employ a non-parametric subsample-based test (Carlstein 1986) using monthly Korean unemployment data during July of 1982 to May of 2015.2 Here, we let Ut denote the monthly unemployment rate at time t = 1,2, ⋯, n. We start by partitioning the sample to obtain the following {Ai},
where kn = [ n2/3 ] . Here [·] is the integer part of a real number. The test statistic that we utilize is the maximal difference between two adjacent block-wise means:
Here, m = [n/kn]. Under some suitable conditions, one can show that
where γm = [4log(m)−2log(log(m))]1/2 and α is the standard deviation of the de-meaned inflation variable. Hence, we reject, at level α , the stability of the NAIRU parameter if
where cα = −log[-−log(1−α)]−0.5 log(π). Here, the standard deviation σ can be estimated with any of the following:
The test results are reported by Table 1. As shown in the table, the results are mixed depending on which estimate is used to estimate σ . While a break is detected under σ = σ2 , there seems to be not enough evidence of a structural break in the Korean monthly unemployment rate when the other two estimates of σ are used instead, as suitably illustrated by Table 1. Unlike other popular structural break tests that utilize some parametric framework, the test considered here is purely non-parametric in that no model structure is required to carry it out. This may have led to the lack of a consensus among the test results.
B. Inference of the Random-Walk Phillips Curve
Given the change-point test results, we undertake the inference of two versions of the Phillips curve: the random-walk Phillips curve and its New Keynesian counterpart. In particular, the random-walk Phillips curve in (2) has been used extensively on the empirical frontier (Staiger, Stock, and Watson 1996, 1997, 2001; Gordon 1997, 1998; Fair 2000; Ball and Mankiw 2002),
where πi and Ui represent the inflation and unemployment rates at time i = 1, ⋯, n, respectively. Here, ϵi is a zero-mean random error at time i, often dubbed the supply shock, and UN and α are unknown parameters. The NAIRU parameter UN embeds all shifts in the inflation-unemployment trade-off. The version in (2) employs only one lagged unemployment value, while multiple lag terms can be introduced without changing the methodology. For simplicity, we use one lag term.
In principle, UN can exhibit substantial variation over time (Gordon 1997, 1998; Staiger, Stock, and Watson 1996, 1997; Ball and Mankiw 2002). To address this possibility, we build on the traditional random-walk-type model (2) and propose the following Phillips curve with the potentially time-varying NAIRU UN(·),
where UN(·) varies over time in its domain [0, 1]. The time-varying NAIRU UN(t) can be estimated by the semi-parametric two-step estimator proposed by Kim (2016),
where Δπi = πi − πi − 1 , and 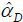 is the differencing estimate of the fixed parameter α in (3). Here,
is the differencing estimate of the fixed parameter α in (3). Here, 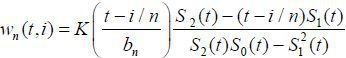 with
with 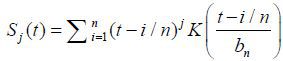 , j = 0,1,2. For the kernel function K (·), we employ the Epanechnikov kernel K(x) = 3max(1− x2 , 0) / 4. The bandwidth bn is established by the generalized cross-validation (GCV) method (Craven and Wahba 1979). The main idea in (4) is that we first estimate α by a first-differencing approach
(Yatchew 1997) and then employ a local-smoothing technique based on the first-differencing estimate
to estimate the unknown trend. We refer to Kim (2016) for details. According to both (4) and Theorem 2 in Kim (2016), the UCB of UN(·) in (3) is constructed as follows:
, j = 0,1,2. For the kernel function K (·), we employ the Epanechnikov kernel K(x) = 3max(1− x2 , 0) / 4. The bandwidth bn is established by the generalized cross-validation (GCV) method (Craven and Wahba 1979). The main idea in (4) is that we first estimate α by a first-differencing approach
(Yatchew 1997) and then employ a local-smoothing technique based on the first-differencing estimate
to estimate the unknown trend. We refer to Kim (2016) for details. According to both (4) and Theorem 2 in Kim (2016), the UCB of UN(·) in (3) is constructed as follows:
(i) Select the bandwidth bn by means of generalized cross-validation (GCV) (Craven and Wahba 1979) and obtain the two-stage semi-parametric estimate (Kim 2016) under the Epanechnikov kernel. To deal with the under-smoothing issue, one can consider a bias-corrected estimator instead.
(ii) Compute 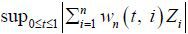 , where the {Zi} values are generated IID standard normal random variables.
, where the {Zi} values are generated IID standard normal random variables.
(iii) Repeat (ii), for instance 1,000 times. We obtain the 95th quantile of the sampling
distribution of 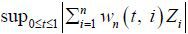 , and denote it as
, and denote it as 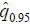 .
.
(iv) Estimate σϵ using the following variant of the subseries variance estimator proposed by Carlstein (1986):
where kn is the length of the subseries and m = [n/kn] is the largest integer not exceeding n/kn . Carlstein (1986) shows that the optimal length of the subseries is 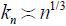 . Hence, we let
. Hence, we let 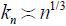 here. For a finite sample, we choose kn = [ n1/3 ]. The asymptotic consistency of
here. For a finite sample, we choose kn = [ n1/3 ]. The asymptotic consistency of 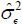 with regard to the long-run variance
with regard to the long-run variance 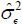 is given by Lemma 5 in Kim (2016).
is given by Lemma 5 in Kim (2016).
(v) According to Theorem 2 in Kim (2016), the 95% UCB of UN(t) is 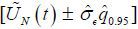 .
.
Note here that the above UCB is more effective in a finite sample than the usual UCB based on the asymptotic results, as that suggested here avoids the problem of slow convergence. For more on this issue, we refer to Theorem 2 and the following discussion in Kim (2016).
C. Inference of the New Keynesian Phillips Curve (NKPC)
For the NKPC side, we consider the hybrid NKPC (Gal´ı and Gertler 1999) based on the unemployment gap. Although it is a theoretically coherent framework, the original NKPC is known to have several empirical limitations, including that related to its ability to forecast inflation. This led to the development of the following hybrid NKPC framework,
where πi and Ui are inflation and unemployment rate at time i = 1, · · · , n, and UN is the NAIRU parameter. Here 0 < φ <1 controls the inflation persistance and δ is related to the parameter that governs the degree of price stickiness. The NKPC proposed in this work is the unemployment-gap-based hybrid NKPC with a time-varying NAIRU UN(·) :
For the inflation series πi in (6), we assume that
where the unknown mean μπ (·) of inflation is Lipschitz-continuous over [0, 1], and the demeaned inflation πi is a mean-zero stationary random process such that
where 𝓕(·) is a measurable function and 𝒯i = (··· , ϵi-2 , ϵi-1 , ϵi ) is the information set available up to time i . The framework in (8) is general such that both linear and non-linear time series
processes such as the ARCH process (Engle 1982) can be represented in this way. Moreover, the de-meaned inflation 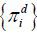 is assumed to have a finite fourth moment. Under (7) and (8), the hybrid NKPC in (6) can be written as follows,
is assumed to have a finite fourth moment. Under (7) and (8), the hybrid NKPC in (6) can be written as follows,
where 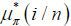 and
and 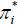 are defined respectively by
are defined respectively by
and
According to (7) and (8), 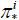 is a mean-zero stationary random process. Moreover, because μπ(·) is Lipschitz-continuous over [0, 1], one can show that
is a mean-zero stationary random process. Moreover, because μπ(·) is Lipschitz-continuous over [0, 1], one can show that
Thus, by applying (12) to (9), we can rewrite the hybrid NKPC with a time-varying NAIRU in (6) as in the following equation:
Here, 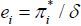 is mean-zero stationary due to the mean-zero stationarity of
is mean-zero stationary due to the mean-zero stationarity of 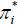 . In addition, the inflation variables in (6) are included as O(1/ n) and ei. Equation (13), derived from the model (6), will serve as the main workhorse in estimating
and constructing the UCB of the NAIRU parameter in the hybrid NKPC here. Given equation (13), we propose a local-linear regression (Cleveland 1979) estimate of the time-varying NAIRU UN(·) because this method minimizes the well-known boundary problem in the kernel-based
regression process. The estimation of UN(·) can be done by the following local-linear regression,
. In addition, the inflation variables in (6) are included as O(1/ n) and ei. Equation (13), derived from the model (6), will serve as the main workhorse in estimating
and constructing the UCB of the NAIRU parameter in the hybrid NKPC here. Given equation (13), we propose a local-linear regression (Cleveland 1979) estimate of the time-varying NAIRU UN(·) because this method minimizes the well-known boundary problem in the kernel-based
regression process. The estimation of UN(·) can be done by the following local-linear regression,
Where 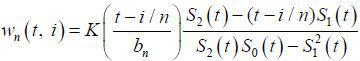 with
with 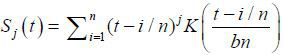 . As in (4), the Epanechnikov kernel is used and the bandwidth is chosen by GCV. The
time domain of t is fixed over t∈[0, 1] and wn(t, i) is the weight given to each observation. The asymptotic consistency of the local-linear
estimate
. As in (4), the Epanechnikov kernel is used and the bandwidth is chosen by GCV. The
time domain of t is fixed over t∈[0, 1] and wn(t, i) is the weight given to each observation. The asymptotic consistency of the local-linear
estimate 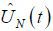 is provided by Kim (2016).
is provided by Kim (2016).
To carry out inference of the NAIRU in (6), one can employ the idea of uniform inference as in the previous section. Given its estimate in (14), the uniform confidence band (UCB) of UN(·) in (6) can be constructed. The theoretic justification of the methodology is provided by the following:
Theorem 1. (Invariance Principle) Let 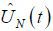 be the estimator from (14). According to
be the estimator from (14). According to 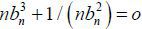 (1) and given the trend-stationarity in (7) and (8),
(1) and given the trend-stationarity in (7) and (8),
where 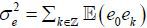 is the long-run variance of
is the long-run variance of 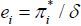 in (13). Here, Zi is an IID standard normal random variable.
in (13). Here, Zi is an IID standard normal random variable.
The main idea in the proof of (15) is provided in the Appendix. The invariance principle
in Theorem 1 states that we can approximate the quantiles of 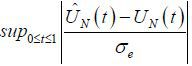 using the quantiles of the sampling distribution of
using the quantiles of the sampling distribution of 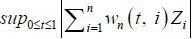 , because we have
, because we have 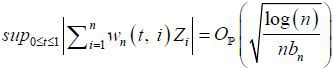 from Kim (2016). This is an important and useful result because it means that we can easily approximate
the quantiles of the proposed test statistic using IID standard normal random variables
instead. Without this result, we have to use the asymptotic distribution of
from Kim (2016). This is an important and useful result because it means that we can easily approximate
the quantiles of the proposed test statistic using IID standard normal random variables
instead. Without this result, we have to use the asymptotic distribution of 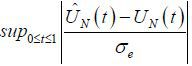 in order to construct the uniform confidence bands of UN(t). However, this approach should be used with great caution because the asymptotic
distribution
in order to construct the uniform confidence bands of UN(t). However, this approach should be used with great caution because the asymptotic
distribution 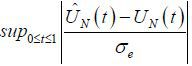 is an extreme-value (or Gumbel) distribution (Kim 2015). It is well known that convergence to this distribution is extremely slow and that
the confidence bands based directly on this distribution could be very inaccurate
if the sample size is not large enough. Given Theorem 1, we propose the following
steps to carry out the uniform inference of NAIRU:
is an extreme-value (or Gumbel) distribution (Kim 2015). It is well known that convergence to this distribution is extremely slow and that
the confidence bands based directly on this distribution could be very inaccurate
if the sample size is not large enough. Given Theorem 1, we propose the following
steps to carry out the uniform inference of NAIRU:
(i) Select the optimal bandwidth bn for our local-linear regression (14) based on the generalized cross-validation (GCV) method (Craven and Wahba 1979).
(ii) Obtain the local-linear estimate 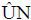 (t) proposed in (14). Here, we use an Epanechnikov kernel.
(t) proposed in (14). Here, we use an Epanechnikov kernel.
(iii) Compute 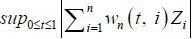 , where wn(t, i) is the weight for local-linear regression in (14), and the {Zi} values are generated IID standard normals.
, where wn(t, i) is the weight for local-linear regression in (14), and the {Zi} values are generated IID standard normals.
(iv) Repeat (iii), for instance 1,000 times. We obtain the 95th quantile of this sampling
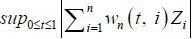 , and denote it as
, and denote it as 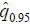 .
.
(v) Estimate σe using the following subseries variance estimator proposed by Carlstein (1986) and extended by Kim (2016),
where kn is the length of the subseries and m = [n / kn] is the largest integer not exceedingn / kn. Carlstein (1986) shows that the optimal length of the subseries is 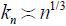 . In practice, we choose kn ∈ (n1/3 , n1/2 ). The asymptotic consistency of
. In practice, we choose kn ∈ (n1/3 , n1/2 ). The asymptotic consistency of 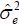 to
to 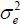 is given by Carlstein (1986) and Kim (2016).
is given by Carlstein (1986) and Kim (2016).
(vi) The 95% UCB of UN(t) is 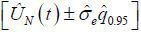 .
.
As in the case of the random-walk Phillips curve, the above UCB is more effective for inference with a finite sample than the usual UCB based on asymptotic results because the proposed method allows us to avoid the problem of slow convergence. The constructed UCB will be used to test various hypotheses regarding the NAIRU, such as the hypothesis that it has been falling since the early 1980s. A detailed description of the data and the empirical results will be provided in the following section.
D. Inflation Forecasting
One of the main purposes of using the Phillips curve in practice is to forecast inflation series. Given the uniform inference procedures developed here, one carry out the forecasting through model validation. If a parametric model is justified through uniform inference, then the model is then used to generate forecasts. If not, alternative semi-parametric fits can be used to forecast the variable. That is, the UCB can provide the model selection criterion for forecasting. Specifically, we propose the following steps to forecast monthly inflation for the Korean economy:
(i) Test for a structural break.
(ii) If there is a break, then reduce the sample to the post-break period. Otherwise, use the entire sample.
(iii) Construct the uniform confidence band (UCB) of the NAIRU parameter.
(iv) Test the null hypothesis of a constant NAIRU based on the constructed UCB.
(v) If the null hypothesis is accepted, inflation is forecast based on the estimate of the constant NAIRU.
(vi) If not, use the average of the non-parametric estimates for the NAIRU to forecast inflation.
In this experiment, we generate point-ahead forecasts of inflation and obtain the forecast errors. A subset of the sample is used to estimate the Phillips curve. Given the estimate, the underlying model is updated to the next time point. Using the first-stage estimate and the updated covariate, the inflation variable is forecast. In principle, the above procedures are applied to the sample after the potential break date only. However, we also apply them to the entire sample for reference such that the forecasting results based on the two samples can be compared.
III. Empirical Results
The data are obtained from the homepage at the Bank of Korea (http://www.bok.or.kr). They include the monthly consumer price index (CPI) and monthly unemployment rate from July of 1982 to May of 2015. The CPI is converted to the monthly inflation rate before it is used with the two Phillips curves. Given the potential break at the end of 1997, the sample is divided into the pre-break period (until the end of 1997) and the post-break period (the remaining sample). In the forecast of inflation, we employ both the entire sample and the sample of the post-break period only. Regarding the inference on the NAIRU parameter, both the random-walk Phillips curve and the new Keynesian Phillips curve (NKPC) are used. First, the inference results for the random-walk Phillips curve and for the NKPC are summarized in Figures 1 and 2, respectively.
FIGURE 1.
TIME-VARYING NAIRU FOR THE KOREAN ECONOMY (JULY 1982 – MAY 2015)
Note: The curve (dotted) in the middle of the band is a local-linear estimate of NAIRU in the Random-Walk Phillips Curve. For the local-linear regression, we use an Epanechnikov kernel. The GCV chooses bn = 0.15. The band (dashed) is 95% uniform confidence band (UCB) of NAIRU. The estimate of NAIRU and the UCB are placed over the monthly unemployment rates (light solid). The fitted horizontal line for a constant NAIRU (dark solid) is U = 3.47.
FIGURE 2.
TIME-VARYING NAIRU FOR THE KOREAN ECONOMY (JULY 1982 - MAY 2015)
Note: The curve (dotted) in the middle of the band is a local-linear estimate of the NAIRU in the New Keynesian Phillips Curve. For local-linear regression, we use an Epanechnikov kernel. The GCV chooses bn = 0.09. The band (dashed) is the 95% uniform confidence band (UCB) of the NAIRU. The estimates of the NAIRU and the UCB are shown over the monthly unemployment rates (light solid). The fitted horizontal line for a constant NAIRU (dark solid) is U = 3.46.
A. Inference of the NAIRU
Figure 1 reports the monthly unemployment data (light solid) and the estimate of the fixed NAIRU (dark solid) in the random-walk Phillips curve. The estimate of the traditional fixed NAIRU for July of 1982 to May of 2015 is 3.47(%). The light-dotted curve is the semi-parametric fit in (4), and the surrounding band (dark-dotted) is the 95% uniform confidence band (UCB) of the NAIRU parameter. As shown in the figure, the semi-parametric fits clearly show the time variation of the NAIRU during this period. The NAIRU decreases during the economic expansion of the late 1980s and the early 1990s. The estimate rises in the late 1990s and reaches its peak just after the 1997 financial crisis. Then, it starts declining again and remains around the fixed estimate from that point. The variation in the cyclical unemployment matches the Korean business cycles during the period, which indicates that the model-based semi-parametric NAIRU estimates are reasonable.
One of the advantages of using the results in Figure 1 is that they enable the uniform inference of the NAIRU. In order to accept a certain null hypothesis for the NAIRU parameter, the null value must be contained by the UCB over the entire period. Otherwise, the null hypothesis is rejected. For example, if the 95% UCB contains the estimate of the fixed NAIRU during the period of July of 1982 to May of 2015, the hypothesis of a constant NAIRU during the period is accepted. If not, the null is rejected at the 5% level. The important point is that the null value must be contained by the UCB during the entire period to be accepted. Figure 1 indicates that the hypothesis of a constant NAIRU is accepted at the 5% level because the fixed estimate is entirely contained within the 95% UCB.
In contrast, Figure 2 illustrates the estimation and inference results under the NKPC during the same period. The estimate of a fixed NAIRU under NKPC is shown by the horizontal line at 3.46%. That is, there is little difference in the fixed NAIRU estimate between the random-walk Phillips curve and the NKPC. As before, the non-parametric estimate of the time-varying NAIRU and its 95% UCB for the NKPC are shown by the light-dotted and dark-dotted curves, respectively. Although they agree in general, the finer results under the NKPC and those based on the random-walk Phillips curve differ. For example, the maximum value of the time-varying NAIRU under the NKPC is higher than that in the random-walk case. However, the increase in the NAIRU at the end of the sample period is higher under the random-walk Phillips curve than in the NKPC case. Otherwise, the results under the different models are in general agreement.
The most noticeable difference between Figure 1 and Figure 2 is that the hypothesis of a constant NAIRU is rejected at the 5% level for the NKPC. The 95% UCB presented in Figure 2 fails to contain the horizontal estimate of a fixed NAIRU at the turn of the century. The dramatic increase in the NAIRU from the late 1990s raises the confidence level as well, and this increase eventually leads to the rejection of the null hypothesis at the 5% level. As noted above, the relatively high increase in the NAIRU estimate under the NKPC during the late 1990s explains why there is a change in the test result. Indeed, Figures 1 and 2 provide useful information regarding the potential variation in the NAIRU. However, they also raise the issue of robustness given the range of possible models to consider in the inference process.
B. Inflation Forecasting
For forecasting inflation based on the Phillips curves, we employ both the full sample (July of 1982 to May of 2015) and the post-break sample (January of 1998 to May of 2015). For each sample, a pseudo-out-of-sample forecasting experiment is conducted based on the random-walk Phillips curve using the first half of the observations.
In each case, both a rolling window of a fixed length and an expanding window with an increasing length are utilized to assess the robustness of the results. To measure the accuracy of point-ahead inflation forecasts, the standard mean-absolute-error (MAE) and the root-mean-squared-error (RMSE) are used. The forecasting results are summarized in Tables 2 and 3. In both tables, “fixed NAIRU” refers to the forecast results under the constant NAIRU, while “time-varying NAIRU” means that the forecasting is carried out through validation of the UCB-based model.
Table 2 shows the forecast results based on the full sample. Each error is divided by the lowest corresponding error. For example, the RMSE under the fixed NAIRU when the expanding window is used is divided by the RMSE under the time-varying NAIRU because the latter is smaller than the former, and so forth. In each case, the error measure under the time-varying NAIRU is lower than that under the fixed NAIRU, indicating that the inflation forecasts obtained through the inference procedure are more accurate than those based on the fixed NAIRU estimate. As shown in Table 3, the same pattern carries over to the case when only the post-break data are used to forecast the monthly inflation. Although the forecast gain is not great in both cases, the results in Tables 2 and 3 confirm that one can clearly benefit from generating inflation forecasts through the UCB-based inference approach suggested in this study.
C. Policy Implications
In macroeconomics, the NAIRU parameter plays an important role because this structural parameter allows us to determine the current status of the economy in the business cycle. If the current unemployment rate is below the NAIRU, the economy is believed to be undergoing an economic expansion. Otherwise, it is in recession. Given an alternative means of estimating and conducting inference on this important parameter, we discuss the policy implications of the empirical results here.
Figures 1 and 2 demonstrate that there are multiple time points during which the unemployment rate is located between the fixed NAIRU estimate and the smoothly varying semi-parametric estimate. From Figure 1, the Korean unemployment rate is above the semi-parametric estimate and below the fixed estimate during much of the first half of the 1990s. According to the fixed NAIRU, the Korean economy expanded during this time. However, the semi-parametric estimate says the opposite: the economy went through a recession. This finding has significant policy implications due to they need to introduce completely different policy changes depending on which estimate to believe. If using the fixed estimate of 3.47%, it becomes necessary to stabilize the economy with certain contractionary policies. If policymakers use the semi-parametric measure instead, they need to stimulate the economy by introducing expansionary policies.
Given these two completely different options on the table, policymakers may want to resort to using the UCB-based inference of the Phillips curve. That is, if the constructed UCB accepts the hypothesis of a constant NAIRU by completely covering it, it may be wise to determine that the economy is undergoing an expansion and to change policies accordingly. In contrast, if the UCB rejects the hypothesis, it would be reasonable to believe that the economy is in a recession and to stimulate it by introducing the proper policies. Given the gravity of the consequence of adopting incorrect policies, it is crucial to decide wisely when determining the status of the business cycle. Clearly, the UCB-based inference methodology in this work can be used to achieve this goal.
Regarding this issue, one also must consider the robustness of the inference. The inference results based on the two models here are quite contradictory: the UCB based on the random-walk Phillips curve accepts the fixed NAIRU hypothesis, whereas that based on the NKPC rejects it. That is, one cannot use the fixed NAIRU estimate for policy analysis if the NKPC is believed to be the underlying model. Given that we understand how different the policy suggestion could be depending on which NAIRU estimate to trust, it is important to be able to determine which model is the true underlying framework. Unfortunately, the methodology developed in this work applies only to the selection of the correct form for the NAIRU parameter. Further research is needed to develop a methodology to determine the proper model framework.
D. Comparison to Business Cycle Measures
Given the potential difference between business cycle decisions based on the traditional fixed NAIRU and the time-varying case, we can compare the results under these two different specifications and the official business cycle decisions announced by the South Korean Government on a routine basis. Among the most standard measures of the business cycle are those by the Korean Statistical Information Service (KOSIS), which are announced every month. The data contain binary values: either zero (i.e., a recession) or one (i.e., an expansion). The sample is trimmed for a comparison between the official decisions by KOSIS and the decisions under our methodology during the period of July of 1982 to July of 2011. The frequency of the data is monthly, which gives us a total of 349 decisions.
We first compare the KOSIS decisions on the Korean business cycle and those made with the time-varying NAIRU estimates in order to observe the percentage of these decisions that matches. Because the original monthly Korean unemployment data are very irregular, we perform some preliminary smoothing before comparing them to the time-varying NAIRU estimates. The data shows that approximately 71 percent of the business cycle decisions during the period of July of 1982 to July of 2011 match, with the number slightly increasing to approximately 73 percent between the fixed-NAIRU-based decisions and the KOSIS announcements.
Two features are noteworthy in this outcome. First, the majority of these decisions based on the different approaches appear to agree in general, although there is also quite a considerable amount of discrepancy among the decisions. In a sense, some degree of difference among the results is predictable because the three methodologies are fundamentally different. Second, the decisions based on the fixed NAIRU hypothesis appear to be marginally closer to the KOSIS decisions than those based on the time-varying NAIRU. One potential reason for this outcome stems from the methodology used for the KOSIS decisions, which is likely to be based on the traditional hypothesis of a “fixed” NAIRU, although we are not entirely sure of the particular methodology employed for the decision. Because we innovate with the traditional fixed-NAIRU assumption in this paper, the results derived under the proposed methodology are likely differ from the decisions based on the traditional assumption regarding the parameter, which is what we observe in this experiment. The reported difference among the business cycle decisions makes it very important to have some reliable inference procedures for the potentially time-varying NAIRU parameter. The methodology proposed in this work can be used to such an end.
IV. Conclusion
In this study, we consider two widely used version of the Phillips curve: the random-walk Phillips curve (Staiger, Stock and Watson 1996, 1997) and the New-Keynesian Phillips curve (NKPC) (Gal´ı, J. and Gertler 1999). We undertake uniform inference of each model and check whether the empirical data support the representative parametric framework. The inference is conducted through the construction of a uniform confidence band (UCB) for the NAIRU. It was found that the widely believed constancy of the NAIRU is rejected under the NKPC for the Korean economy, whereas parameter constancy is accepted under its random-walk counterpart.
We apply the developed methodology to inflation forecasting. If the parametric fit is entirely covered by the constructed UCB, the in-sample fit is extended out-of-sample to forecast the inflation variable. If the fit is not covered by the UCB, we resort to the averaged semi-parametric fits of the time-varying NAIRU. In a pseudo-out-of-sample forecasting experiment conducted here, the forecasts under this method and those under the traditional random-walk Phillips curve are compared to assess their relative advantages. For both the entire sample and the post-break sample, the UCB-based forecasts are found to be superior to those based on the traditional approach. The superiority of the UCB-based forecasts persists under both the rolling-window and expanding-window schemes.
The current project leaves a number of interesting topics for potential future research. First, the paper uses the uniform inference methodology to choose between the fixed NAIRU estimate and the smoothly time-varying cases for inflation forecasting. In fact, the presence of structural breaks is highly likely in the Korean economy. At the same time, both the number of potential breaks and their dates are uncertain. To address this uncertainty, one can perform forecast averaging based on the UCB. Assuming that any date in the sample could be a potential break date, we forecast based on parametric models with breaks that are justified by the UCB only. The forecasts accepted by the UCB are then combined through averaging. Because this approach handles model uncertainty via an averaging method, the accuracy of the forecasts could be higher than that of the forecasts here.
Another interesting extension would be to develop a methodology for selecting the correct Phillips curve in the beginning. The current work assumes that the correct Phillips curve to use is either the random-walk curve or the NKPC. Inference is then conducted on the model parameter. In this sense, the approach here is semi-parametric. However, no justification of the assumption is provided in the current work. As shown in Figures 1 and 2, the inference outcome could be rather model-sensitive, and it lacks in robustness. By providing some reliable guideline on the issue, we can make the current result more robust and reliable from the perspective of policy analysis. Further insight can be gained by extending the work in these and in other directions.
Appendices
The proof of Theorem 1 is based on the trend-stationarity of the inflation variable and the invariance principle in Kim (2015). We provide here only a sketch of the proof. For details of the proof, we refer the reader to Kim (2015).
Proof of Theorem 1
Recall that we have the hybrid NKPC in equation (9) due to (7) and (8). By performing a Taylor’s expansion on UN(·) in (9), we can show the following,
where C is some constant. The last equality is due to the smoothness of the NAIRU, the Lipschitz-continuity of the kernel, and Lemma 2 in Kim (2015). Then, according to 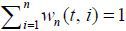 , we have
, we have
Then, with 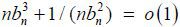 ,
,
which leads to
Notes
Kim gratefully acknowledges funding from the National Research Foundation of Korea Grant by the Korean Government (NRF-2015S1A5A8014208).
The model originates from the expectations-augmented Phillips curve (Friedman 1968; Phelps 1970).
References
, & (2015). Was it Risk? Or was it Fundamentals? Explaining Excess Currency Returns with Kernel Smoothed Regressions. Journal of Empirical Finance, 34, 99-111, https://doi.org/10.1016/j.jempfin.2015.08.007.
, & (2002). The NAIRU in Theory and Practice. Journal of Economic Perspectives, 16, 115-136, https://doi.org/10.1257/089533002320951000.
(1986). The Use of Subseries Values for Estimating the Variance of a General Statistic from a Stationary Sequence. The Annals of Statistics, 14, 1171-1179, https://doi.org/10.1214/aos/1176350057.
(1979). Robust Locally Weighted Regression and Smoothing Scatterlpots. Journal of the American Statistical Association, 74, 829-836, https://doi.org/10.1080/01621459.1979.10481038.
(1982). Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica, 50, 987-7007, https://doi.org/10.2307/1912773.
(2000). Testing the NAIRU Model for the United States. The Review of Economics and Statistics, 82, 64-71, https://doi.org/10.1162/003465300558632.
(1984). Forward and Spot Exchange Rates. Journal of Monetary Economics, 14, 319-338, https://doi.org/10.1016/0304-3932(84)90046-1.
, & (1999). Inflation Dynamics: A Structural Econometric Analysis. Journal of Monetary Economics, 44, 195-222, https://doi.org/10.1016/S0304-3932(99)00023-9.
(2016). Inference of the Trend in a Partially Linear Model with Locally Stationary Regressors. Econometric Reviews, 35(7), 1194-1220, https://doi.org/10.1080/07474938.2014.976530.
(1998). Why is the U.S. Unemployment Rate so much Lower? NBER Macroe conomics Annual, 13, 11-61, https://doi.org/10.1086/ma.13.4623732.
, , & (1997). The NAIRU, Unemployment and Monetary Policy. Journal of Economic Perspectives, 11, 33-49, https://doi.org/10.1257/jep.11.1.33.
(1997). An Elementary Estimator of the Partial Linear Model. Economics Letters, 57, 135-143, https://doi.org/10.1016/S0165-1765(97)00218-8.