
Defending Multiple Terrorist Targets
Abstract
This paper analyzes a situation where multiple targets are exposed to a potential terrorist attack. The probability of an attack is determined endogenously in a game where a terrorist chooses the target while the targets independently determine the level of deterrence. As each target tries to divert an attack to others, the symmetric equilibrium becomes suboptimal and exhibits dispersion in the level of deterrence. The analysis shows that the first best deterrence level may be achieved when the targets can write a binding risk-sharing contract. Such a contract has limited applicability however as it suffers from a potential verification problem.
Keywords
Terrorism, Counterterrorism, Contract, 테러리즘, 대테러, 계약
JEL Code
D74, H56
Ⅰ. Introduction
A series of recent events has made terrorism a subject of increased academic interest. The dominant theme in the literature has been the analysis of various strategic interactions among the players in the scene. This article aims to provide an analytical framework that incorporates two of such interactions: the one between a terrorist and the targets and the one among the targets themselves.
The model considers a situation in which many identical targets are exposed to a potential terrorist threat. The game starts when a terrorist observes the cost of operation. Comparing its cost and the benefit, the terrorist decides whether to initiate an operation or not. Each target invests in deterrence without knowing the terrorist’s decision. An operation is completed when the terrorist launches an attack against one of the targets. Two questions emerge naturally: i) is the outcome of the game desirable from the targets’ perspective?, and ii) if not, is there any way in which the targets can improve their fate?
The answer to the first question turns out to be negative. The targets’ problem comes from two different sources. First, the targets do not internalize the negative externalities when they make their investment decisions. In equilibrium, each target tries to outinvest others knowing that the weakest target will be the victim of an attack. The possibility of this attack-diversion has been recognized in the literature (Sandler, 2003). When every target tries to undercut others, however, no target can actually succeed in the attempt. Consequently, they all end up playing a mixed strategy in the symmetric equilibrium of the game. Moreover, an attack occurs with a lower probability compared to the hypothetical case where the targets coordinate their actions. In other words, there is too much deterrence in equilibrium.
The second problem facing the targets results from the fact that they cannot credibly commit to their actions. The idea, which dates back to Schelling (1960), is certainly not new. Given that the terrorist’s decision depends on his belief about the targets’ choice, the targets would do better if they could convince the terrorist that an attack is not likely to succeed. But this requires that the targets maintain an excessive level of investment even when the risk of an attack has been kept low. Such a strategy, however, will not be credible and hence cannot succeed in equilibrium.
The targets can mitigate or sometimes even completely resolve the problem by writing a binding contract among themselves. Assuming that neither the targets’ investment nor the level of deterrence is verifiable, the only feasible contracts have the form of a risk-sharing scheme. When the victim’s identity can be verified regardless of the outcome of an attack, such a contract can restore the efficiency as long as the first best does not require a complete deterrence. If the identity of a failed attack cannot be verified, however, the targets may achieve the coordination outcome but not the first best. It is argued that this verification problem becomes more severe when the targets involved are sovereign states rather than private parties.
There is a growing literature on game-theoretic analysis of terrorism (Arce and Sandler, 2005; Heal and Kunreuther, 2005; Keohane and Zeckhauser, 2003; Konrad, 2004; Rosendorff and Sandler, 2004; Siqueira, 2005). For a survey of earlier studies, see Sandler and Enders (2004). Most of existing literature focus on a single aspect of the strategic interactions such as the one among the targets, among the terrorist groups, or the one between a target and a terrorist group. A notable exception is Bier et al. (2007), which considers a model with a terrorist and two potential targets. In their model, the terrorist is assumed to pick a specific target at the same time when he makes the operational decision. This difference in modeling strategy is discussed further in the next section. By comparing the outcomes of a simultaneous and sequential move games, they show that the targets can enjoy a strategic advantage by moving first. But neither the commitment issue nor its potential remedies is explicitly examined in their article.1
The idea that the government may correct the attack-diverting externalities by subsidizing terrorism insurance is explored in Lakdawalla and Zanjani (2005). But the strategic interaction between the terrorist and the targets is not analyzed explicitly in their model. Consequently, a budget-balancing subsidy scheme is shown to implement the first best, which is not the case in this article where the targets’ choice is constrained by the commitment problem. The techniques used to characterize the equilibrium distribution function are similar to those in Varian (1980). Due to the differences in the context, however, there are significant changes in the details including the construction of the support of the distribution function.2
The rest of the article is organized as follows. Section 2 introduces the basic model. The symmetric equilibrium of the game is characterized in section 3. The welfare property of the equilibrium as well as the feasibility of contracting solution are analyzed in section 4. Concluding remarks follow in section 5.
II. Model
There is a terrorist group (= terrorist) and n ≥ 2 potential terrorist targets (= targets). The game proceeds as follows. In the first stage, the terrorist draws a type θ∈[θ,θ] from a known distribution. The type determines the cost of carrying out a terrorist operation. After observing the type, the terrorist decides whether to start an operation or not. Neither the terrorist’s type nor his action in the first stage is observed by the targets. In the second stage, each target makes investment to enhance its capability to deter a future attack. In the third stage, the terrorist chooses a specific target and launches an attack.
A target incurs a loss of D > 0 if an operation succeeds and zero if it fails. An attack against target i becomes a success with probability pi. Failure may occur either during the preparation stage of an operation or at the time of an attack. The first case arises because an operation may be detected before its completion. The second case includes a situation in which an attack is defeated by the target as well as the one in which failure occurs from a natural cause (e.g., a bomb does not go off due to malfunction).
By investing in deterrence efforts, each target can reduce its success probability pi. The cost of investment is given by a twice continuously differentiable function c(pi), which is strictly decreasing and convex. Three additional assumptions are made: i) limp→0c'(p) + D < 0, ii) D < limp→0c(p), and iii) there exists a pmax ∈ (0,1] such that c(p) = 0 for p ∈ [pmax, 1] and c' (pmax) = 0. The first (second) condition is satisfied when the marginal (total) cost gets sufficiently large near p = 0. The third condition requires that both total and marginal cost become zero as p approaches 1.
The terrorist maximizes the targets’ expected loss net of his cost of operation θ. The terrorist’s type θ∈[θ,θ] is his private information but its distribution G(θ) is known to the targets.G(θ) is strictly increasing and twice continuously differentiable with 2G'(θ) + G''(θ) >0. The condition, which guarantees that the first-best solution is well-defined,
is satisfied if the distribution function is not too concave. Two additional assumptions
are made: i) pmin ≡ 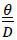 <pmin and ii) pmin <
<pmin and ii) pmin < 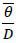 . The first (second) condition implies that an operation must be worthwhile (not worthwhile)
for the terrorist when the cost is sufficiently small (large). It rules out rather
trivial cases where either an attack never occurs or it occurs always in equilibrium.
. The first (second) condition implies that an operation must be worthwhile (not worthwhile)
for the terrorist when the cost is sufficiently small (large). It rules out rather
trivial cases where either an attack never occurs or it occurs always in equilibrium.
In the first stage, the terrorist decides whether to start an operation (s = s1) or not (s = s0) . Given that an operation has been initiated, the terrorist picks a specific target for attack in the third stage. In order to maximize the targets’ expected loss, the terrorist should attack the most vulnerable target. In other words, the terrorist will choose a target k if and only if
When more than one targets have the highest probability of success, the terrorist is assumed to pick one of the targets randomly.
In any Perfect Equilibrium of the game, the terrorist’s optimal decision in the third stage must be taken into account by the targets. Given that an attack occurs only when there is an ongoing operation, a target’s payoff depends on whether the terrorist initiated an operation or not. Let Li be target i’s total loss, i.e., the sum of the cost of investment and the expected loss from an attack. Then Li is given by
where
By setting the probability of success at pi, target i incurs a cost of c(pi). The second term in the expression, I(s)ρi(p1,..., pn)piD, follows from the fact that loss from an attack materializes only when i) there is an ongoing operation (s =s1), ii) target i is the weakest among n potential targets, and iii) the attack turns out to be successful. The joint loss of the targets is obtained by adding up the individual target’s loss:
Targets are allowed to play mixed strategies. The strategy of target i then becomes a distribution function Fi(p) with a support in [0,1].
In the first stage, the terrorist makes his operational decision. For a given cost of operation θ, the terrorist should initiate an operation if
or
where the expectation is taken with respect to p = {p1,..., pn}. The optimal decision follows a cutoff rule: an operation is initiated if and only if the cost of operation does not exceed the targets’ expected loss from an attack.
Since the targets do not observe the terrorist’s choice in the first stage, there is asymmetric information between the terrorist and the targets. The outcome of the game hence depends on how the targets form their beliefs about the state of the game in the second stage. The relevant equilibrium concept is weak Perfect Bayesian Equilibrium. It requires two conditions: sequential rationality and belief consistency. The first is satisfied if each player makes an optimal decision in every information set. The second condition requires that beliefs should be consistent with equilibrium strategies. Let μ be the targets’ belief that there is an ongoing operation, i.e., s = s1. The equilibrium condition is then summarized as follows.
Definition The weak Perfect Bayesian Equilibrium of the game is defined as follows:
The first condition guarantees that the targets’ belief is consistent with the terrorist’s equilibrium strategy in the first stage. In equilibrium, the terrorist uses a cutoff rule to make his first-stage decision. For consistency, therefore, the targets’ belief ( = μ*) must coincide with the actual probability of attack, which occurs when the terrorist’s cost is lower than the equilibrium cutoff ( = θ*). The second condition shows the optimality of the terrorist’s choice while the third condition gives that of the targets. The optimal cutoff is found where the terrorist becomes indifferent between the two choices s0 and s1. Each target should minimize its expected loss by choosing a distribution over p. Notice that the terrorist’s optimal decision in the third stage is subsumed in the second-stage game and hence omitted in the equilibrium definition.
Before closing this section, it seems appropriate to add a brief remark on the modeling strategy. A distinguishing feature of the game examined in this article is that the terrorist makes his decision in two steps. In the first stage, the terrorist decides whether to participate in terrorist activities. Participation requires a sunk cost, which can be interpreted as the opportunity cost of doing the terrorism business. The decision in the third stage, on the other hand, is assumed to be tactical in nature which can be made flexible depending on the observed strength of the targets.
The advantage of this approach is that it allows one to capture the two sources of inefficiency—attack-diverting externalities and commitment problem—at the same time. One can easily confirm this by examining the consequences of adopting alternative strategies. Consider first the case in which the third stage is merged into the first stage. This implies that the terrorist picks a target without knowing each target’s strength. Given that its strength cannot be observed by the terrorist, there will be no incentive for a target to out-invest others hence attack-diversion effect will disappear. If the first stage is merged into the third stage instead, the targets become the first-mover in the game and hence have the commitment power. By construction, the commitment problem does not arise in this case.
III. Equilibrium
The first step for characterizing the equilibrium is to show that an attack occurs with a positive probability, i.e., μ* > 0. This can be easily shown by examining the implication of assuming the contrary. If the targets believe that an attack never occurs, there is no point of investing in deterrence. Therefore, only the success probabilities higher than pmax must be played in equilibrium. But this implies
Given the assumption pmaxD > θ, however, the terrorist should attack with a positive probability because Pr(θ ≤ θ*) ≥ Pr(θ ≤ pmaxD) > 0. This shows that the belief μ* = 0 cannot be consistent with the terrorist’s strategy because PrPr(θ ≤ θ*) =μ* in equilibrium.
One of the distinctive features of the model is that a target can divert a potential attack to others. Consequently, each target has an incentives to slightly ‘undercut’ other targets’ probabilities. With every target trying to out-invest others, one may expect that an equilibrium in pure strategies would be difficult to sustain. It turns out that this is the case indeed.
Lemma 1 There is no equilibrium in which the targets use pure strategies.
Therefore an equilibrium, if exists, must be in mixed strategies. In a mixed-strategy equilibrium, each target uses a distribution function to randomize over success probabilities. Although the model assumes that targets are identical, one cannot exclude in general the possibility that they use different distribution functions in equilibrium. To keep the analysis tractable, however, the following discussion will focus only on symmetric equilibria of the game where the targets use the same distribution function. Let F*(p) be the equilibrium distribution function.
For an equilibrium to be sequentially rational, the game needs to be solved backwards starting from the last stage. Once the outcome of the third stage is already embedded in the targets’ payoff, the second stage becomes effectively the last stage of the game. The following lemma gives the first result regarding the targets’ equilibrium choice.
Lemma 2 There is no jump in the equilibrium distribution function.
Similar to the case with pure strategies, the intuition is again that a jump in a distribution function will provide an opportunity to undercut others’ probabilities. Without a jump, the distribution function becomes continuous and the probability of a tie becomes negligible. This makes it possible to express a target’s equilibrium loss in a much simpler form. For a given belief μ > 0, it follows that
The first equality uses the definition Es[I(s)] = μ. The second equality follows from the fact that target i becomes the weakest among all targets with probability F*(pi)n-1.
Let Lmax(p) ≡ c(p) + μpD. Lmax(p) can be interpreted as the maximum possible loss of a target when it sets a success probability p with certainty. It is the sum of the investment cost c(p) and μpD, which equals the expected loss from an attack when a target expects to be the weakest for sure. Notice that Lmax(p) is strictly convex given the assumption c''(·) > 0. Associated with this function are the following two quantities p and p, which play a crucial role in the analysis:
Lemma 3 For a given μ, p and p are uniquely determined. Both p(μ) and p(μ) are continuously differentiable with respect to μ.
It turns out that the interval formed by the two values [p, p] becomes the support of the equilibrium distribution. A formal proof, which is given in the appendix, requires several steps of reasoning. The main intuition, however, comes from the basic property of a mixed-strategy equilibrium: the targets must be indifferent among all pure strategies played with a positive probability. In particular, this implies that a target should be indifferent between playing only the minimum and the maximum p in the support of the equilibrium distribution. Let pm (pM) be the minimum (maximum) respectively. Since a target becomes the strongest (weakest) by setting p = pm (p = pM), it follows that c(pm) = c(pM) + μpMD.
Assuming that there is no ‘gap’ between pm and pM, the support [p, p] can be verified by showing that pm= p and pM = p. Given that Lmax(p) is strictly convex and reaches its minimum at p, it is strictly decreasing (increasing) for p<p(p>p). If the maximum pM does not coincide with p, then it must be that c(pM)+μpMD> c(p) + μpD. If a target sets p = p, however, the expected loss will be at most c(p) + μpD contradicting the assumption that p = pM is played in equilibrium. A similar argument can establish the minimum p. Suppose to the contrary that the minimum pm is not equal to p. By construction, the expected loss at the maximum pM = p is equal to the cost of investment at p, i.e., c(p) = c(p) + μpD. Given that c(⋅) is strictly decreasing, however, this implies c(pm) ≠ c(p) + μpD. This is again a contradiction because it violates the indifference condition c(pm) = c(pM)+μpMD. The last step is to check whether there exists a gap in the support. The proof in the appendix shows that such a gap cannot arise in equilibrium given the convexity of c(⋅).
Once p is known to be the maximum in the support, it is straightforward to solve for the equilibrium distribution function. Given that the expected losses must be equalized across all p’s in the support, it follows that
or
For a given belief μ, therefore, the targets’ behavior is completely characterized by the distribution function F*(p;μ).
In the first stage, the terrorist makes his decision expecting the targets’ choice in the next stage. An operation is initiated if and only if the cost of operation does not exceed the targets’ expected loss from an attack. The optimal cutoff is given by
The expression involves an order statistic max{p1,..., pn}, which has a distribution function {F*(p;μ)}n. Then the optimality condition for the terrorist can be written in a simpler form as
Notice that the dependency of the optimal cutoff on the targets’ belief is made explicit in the expression θ*(μ).
The equilibrium of the game is found where the targets’ belief becomes consistent with the terrorist’s optimal strategy. This requires that the equilibrium belief μ* should satisfy
Given that G(⋅) is strictly increasing, the condition can be also written as
where G-1(⋅) is the inverse of G(⋅).3
Proposition 1 The symmetric equilibrium of the game is characterized as follows:
where p* is implicitly defined by c(p*) ≡ c(p*) + μp*D and p* ≡ argmin c(p) + μ*pD.
IV. Analysis
From the targets’ perspective, the outcome of the game is not satisfactory for two reasons. In equilibrium, each target tries to divert an attack to others, which results in a dispersion in the level of investment. The joint expected loss may be reduced further if the targets can coordinate on their efforts. In addition to this coordination problem, the targets suffer from a commitment problem that keeps them from achieving the first-best outcome. Given that the probability of an attack depends on the terrorist’s belief about the targets’ investment, the targets could lower their expected loss if they could commit to a high level of investment. But such a scheme requires that the targets should maintain the investment high even when the risk of an attack remains low. The targets’ strategy will fail, therefore, unless they have a proper mechanism to support the commitment.
To identify each of these issues separately, two hypothetical models are considered in the following analysis. The first model assumes that the targets can coordinate their investments but cannot commit to a certain investment level. The second model allows for both coordination and commitment. The analysis then proceeds to examine whether contracts can be designed to eliminate the two types of inefficiencies.
1. Equilibrium with Coordination
The terrorist and the targets play the same game as before except that the targets minimize the joint expected loss by coordinating their actions. The targets’ strategy is to choose a joint distribution function F(p) defined on an n-dimensional unit cube [0,1]n. Notice that this allows for the possibility that two or more targets’ choices are correlated with each other. There is no change in the terrorist’s problem in the first- and the third stage of the game.
When coordination is allowed, the targets must set the same investment level across all targets. Given that only the weakest target will be attacked by the terrorist, investing more in one target than in others would be simply meaningless. More formally,
Lemma 4 In any equilibrium with coordination, the targets choose p1 = p2 = ... = pn with probability 1.
Without loss of generality, therefore, one may restrict attention to a one-dimensional distribution function to examine the targets’ problem. Then the joint expected loss can be written as
The integrand is strictly convex hence has a unique minimum. Let pc(μ) argmin nc(p) + μpD. This implies that the joint expected loss will be minimized if pc(μ) is set across all targets.
The terrorist’s choice in the first stage follows a cutoff rule. The optimal cutoff has a simple form in this case:
θc(μ) = ∫[0,1]n max{p1,..., pn}DdFc(p)=pc(μ)D.
The equilibrium of the game is determined by finding a consistent belief μc that satisfies
Proposition 2 The equilibrium with coordination is characterized as follows:
i) μc ∈ (μ*, 1) is uniquely determined by G (θc(μc)) = μc
ii) s = s1 if and only if θ ≤ θc (μc) = pcD
iii) the targets set p1 =p2 = ...= pn = pc∈ (pmin, pmax) with probability 1
where pc ≡ argmin nc(p) + μcpD.
The difference with the equilibrium in the basic model is that now the targets internalize the attack-diverting externalities by coordinating their actions. As a consequence, the investment becomes equalized across all targets and hence the dispersion in deterrence level is no longer observed in equilibrium. Another interesting feature of the equilibrium is that an attack becomes more likely when coordination is allowed, i.e., μc > μ*. The lack of coordination leads to an over-investment in deterrence efforts.
2. Equilibrium with Coordination and Commitment
Although coordination will certainly help, it does not exhaust all the possibilities for improvement. The targets’ problem with coordination is given by
The targets minimize the joint expected loss taking their belief μ as given. But the probability of an attack, which must coincide with the targets’ belief in equilibrium, depends on the terrorist’s belief about the targets’ action. This suggests that the expected loss could be reduced further if the targets were able to control the terrorist’s belief directly.
Consider a modified game where the targets can commit to their choice before the terrorist makes his first move. The rest of the game is the same as before and the targets are assumed to coordinate their decisions. In the new game, therefore, there is an additional stage in which the targets are allowed to make their commitment.
The outcome of the modified game depends on whether such a commitment can be made credible by the targets. A commitment will have no effect in equilibrium, for instance, if the targets can costlessly withdraw from whatever claim they made in stage zero. This implies that the targets will discard any previous commitment that requires a suboptimal action in the second stage. The only credible commitments in this case must be the ones that would have been chosen in the second stage even without making them in the first place.
If there is a way to make a credible but non-trivial commitment, however, the targets can have a strategic advantage over the terrorist. Suppose that such a commitment has been made by the targets in stage zero. Since the investment must be equalized across all targets with coordination, one may restrict attention to a common success probability p. Given that the commitment is credible, the terrorist will initiate an operation if and only if the cost of operation θ does not exceed its benefit pD. Then an attack will occur probability Pr(θ ≤ pD= G(pD). But this must be expected by the targets in the commitment stage. The targets’ problem then becomes
The objective function correctly reflects the fact that the targets’ choice changes the probability of an attack in equilibrium. Committing to a lower p will influence the terrorist’s belief and hence decrease the probability of an attack. In equilibrium, therefore, the targets will invest more in deterrence compared to the case where only coordination is allowed.
Proposition 3 The equilibrium with coordination and commitment is characterized as follows:
i) μo ∈ [0, μc] is uniquely determined by G(θo) = μo
ii) s = s1 if and only if θ ≤ θo = poD
iii) the targets set p1 =p2 = ...= pn = po∈ [pmin, pc) with probability 1
where po ≡ argmin nc(p) + G(pD)pD.
Compared to the case where only coordination is allowed, the targets invest more in deterrence when they can also commit to their actions. An attack becomes less likely as a result and it may even become totally prevented (μo = 0) in equilibrium. In either of the two previous equilibria, on the other hand, an attack always occurs with a positive probability. As will be shown shortly, however, a complete deterrence turns out to be quite difficult to achieve in practice.
3. Contracting
The analysis so far has shown that the targets may improve their fate if they can successfully coordinate and commit to their actions. Given that each target has an incentive to pursue its own interest at the expense of others, what remains to be shown is exactly how they may achieve the coordination and commitment.
The answer will be rather straightforward if the targets can write a binding contract on their investment. If a contract requires that each target should invest to set pi = po, the first-best will be attained as long as a large enough penalty is imposed for a breach. To implement the contract, however, the court should be able to verify the investment made by the targets. The problem is that the investment, which may include the amount of “efforts” as well as monetary spending by the targets, will be difficult to measure and hence to verify. Alternatively, a contract could be written directly on pi’s. But verifying them in court will not be an easy task either.
A more realistic approach would be to write a contract based on the outcome of an attack. A contract then must specify a transfer payments between the victim and the rest of the targets. The payments will depend on the three contingencies of the game: i) an attack occurs and succeeds, ii) an attack occurs but fails, and iii) no attack occurs. Let B(b) be the payment made by the victim (other targets) after a successful attack and B′(b′) be the payment made by the intended victim (other targets) after a failed attack. If an attack does not occur, there is no victim to be treated differently. Define a to be the payment imposed on all targets in this case. A payment can be negative, which will be the case if a target receives a transfer from others.
To make such a contract enforceable, the identity of the victim needs to be verified. It will be easy to identify the victim once damage has been made by an attack. It may not be so, however, when an attack has been attempted but failed. There are two cases to consider. If the attack was defeated by the target on site, the identification will not be much of a problem. If the operation has been detected before completion, on the other hand, verifying the incident let alone the intended target could be problematic. In the following analysis, the optimal contract will be characterized first under the assumption that all three contingencies can be verified. The case when the second and the third contingency cannot be differentiated will be discussed later.
Without any restrictions on the structure, a contract may specify transfer amounts that are not consistent with each other. For instance, it may happen that a target is entitled to a positive transfer that exceeds the amount of payments made by the rest of the targets. This motivates a concept of budget-balancing contracts. More formally, a contract is called budget balancing if the payments of all targets sum up to zero in each contingency. This implies that a budget-balancing contract must satisfy three conditions: i) B +(n-1)b = 0, ii) B′ +(n-1)b′ = 0, and iii) na = 0. An immediate consequence of this restriction is that a must be equal to zero, i.e., there should be no transfer among the targets in case an attack has not occurred.
Consider a situation where the targets play the same game as in the basic model except that now they can write a binding contract before the terrorist makes his first move. The question is whether there exists a budget-balancing contract that can help the targets achieve their first-best. It turns out that such a contract does not exist.
Proposition 4 Suppose that μo > 0. Then the first best can be implemented by a budget-balancing contract. In such a contract, b′ > 0.
The fact that an optimal contract should set b′ > 0 has an interesting implication. Given the budget-balancing condition, this means that B′ =-(n-1)b′ < 0, i.e., a contract should specify a positive transfer to the ‘victim’ of a failed attack. To enforce the clause, however, the court must be able to verify whether there has been such an attempt, and if so, the identity of its intended target. As is pointed out earlier, however, verifying a failed attack may not be an easy task especially when the operation failed because it was detected before completion.
To examine the consequences of this problem, suppose now that the victim’s identity cannot be verified in a failed attack. Then a contract must specify the same transfer payment for all targets in case there has been an unsuccessful attempt by the terrorist, i.e., B′ = b′. But this implies that B′ = b′ = 0 because the payments must satisfy the budget-balancing condition B′ =(n-1)b′ .
Corollary Suppose that μo > 0. If the victims cannot be verified in failed attacks, there is no budget-balancing contract that implements the first best.
V. Concluding Remarks
The analysis has shown that the commitment problem faced by the targets makes it difficult to eliminate terrorism risk completely. Absent an imminent threat, targets cannot be expected to make sufficient amount of deterrence efforts, which makes them vulnerable to a potential terrorist attack. Although complete deterrence may not be optimal for the targets, this finding does exemplify the limitations of defensive counterterrorism policy.
Contracting turns out to be an effective instrument that can be used to mitigate the targets’ problem. An implicit assumption, however, is that such a contract will be signed by all of the targets exposed to a common terrorist threat. Even though the contracting is to achieve a collective good, reaching an agreement may not be an easy task especially when many parties are involved in the process. Moreover, for a contract to function properly, it must contain a clause that penalizes a party who withdraws later. Otherwise, every target will find it irresistible to withdraw from the contract and slightly undercut the other targets. Such a deviation will be profitable because, with only a minor increase in the deterrence investment, the deviant will never incur the loss from an attack nor the transfer payment to other targets. If the targets involved are subject to a common authority, the problem may be resolved by making the participation mandatory. Examples would be private parties in a single country and local/state governments under a federal government. If the targets involved are different sovereign states, however, participation must be voluntary. Without sufficient contractual penalties, therefore, cooperation will be difficult to maintain in this case.
Another issue regarding the implementation of an optimal contract is that it requires the verification of the victim’s identity in both successful and failed attacks. The victim needs to be rewarded in a failed attack because it will provide additional incentive for deterrence, which is necessary to achieve the first best. Verifying the victim could be problematic, however, especially when a failure is caused by detection instead of defeat. Given that verification matters to the extent that it affects the targets’ incentives, the problem will become most severe when the targets’ deterrence depends heavily on detection rather than defeat. But detecting terrorist operations, which requires sophisticated intelligence capabilities as well as the authority to apply them, is mainly the responsibility of the government. This suggests that cooperation might be more difficult to achieve among different countries than among private parties in a single country.
Terrorism is a complicated subject which involves multidimensional strategic interactions. This article examines two of such interactions in a unified framework. Although the analysis is carried out in a stylized model with a single terrorist group and multiple identical targets, the main finding—resolving the coordination and the commitment problem at the same time is in general difficult—seems to be robust. It would be of interest to see whether a more sophisticated mechanism can be found which may improve upon the simple contracts considered here.
From a counterterrorism perspective, this article deals only with defensive measures as opposed to proactive measures (Rosendorff and Sandler, 2004). A more complete picture will be obtained if both types of measures are incorporated into the model. Such analysis will be best performed in a dynamic setting where terrorists and targets interact over time. The approach adopted in Keohane and Zeckhauser (2003) seems particularly promising in this respect. These are some of the questions left for future research.
Appendices
Appendix
Proof of Lemma 1
Suppose not. Then there exists a p* = (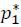 ,...,
,..., 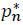 ) such that target i sets
) such that target i sets 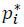 with probability 1 in equilibrium. It suffices to consider the case μ*> 0. Notice first that
with probability 1 in equilibrium. It suffices to consider the case μ*> 0. Notice first that 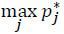 ≤ pmax in this case. If
≤ pmax in this case. If 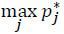 > pmax, the target with the highest probability may reduce its expected loss by choosing
> pmax, the target with the highest probability may reduce its expected loss by choosing
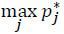 - ε. This is because, for a small enough ε > 0, the expected loss from an attack will decrease while the cost of investment
will remain constant. But this in turn implies that
- ε. This is because, for a small enough ε > 0, the expected loss from an attack will decrease while the cost of investment
will remain constant. But this in turn implies that 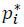 = p* for all i. To confirm, suppose to the contrary that
= p* for all i. To confirm, suppose to the contrary that 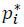 <
< 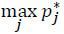 for some i. Then target i’s cost of investment must be strictly decreasing for pi ∈ (
for some i. Then target i’s cost of investment must be strictly decreasing for pi ∈ (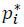 ,
, 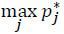 ) because
) because 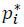 <
< 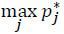 ≤ pmax. This means that target i can lower its expected loss by setting
≤ pmax. This means that target i can lower its expected loss by setting 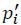 =
= 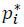 + ε instead of
+ ε instead of 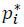 . As long as ε > 0 is small enough to satisfy
. As long as ε > 0 is small enough to satisfy 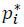 + ε <
+ ε < 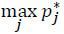 , target i can reduce its cost of investment by c(
, target i can reduce its cost of investment by c(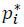 )-c(
)-c(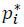 +ε) without changing the probability of being attacked. The assumption
+ε) without changing the probability of being attacked. The assumption 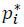 <
< 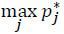 hence leads to a contradiction. Hence, the only remaining possibility becomes
hence leads to a contradiction. Hence, the only remaining possibility becomes 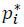 = p* ≤ pmax for all i. But this is not consistent with equilibrium, either. Suppose that such an equilibrium
exists. Then the expected loss of each target must be c(p*) +
= p* ≤ pmax for all i. But this is not consistent with equilibrium, either. Suppose that such an equilibrium
exists. Then the expected loss of each target must be c(p*) + 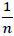 μ*p*D. If a target undercuts p* by ε > 0, however, it can divert a potential attack to others with probability 1. The
total expected loss will become c(p*- ε), which will be smaller than the equilibrium loss c(p*) +
μ*p*D. If a target undercuts p* by ε > 0, however, it can divert a potential attack to others with probability 1. The
total expected loss will become c(p*- ε), which will be smaller than the equilibrium loss c(p*) + 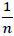 μ*p*D for a small enough ε > 0. □
μ*p*D for a small enough ε > 0. □
Proof of Lemma 2
The proof is essentially the same as the one in Varian (1980). Suppose that there is a jump at p. Since there can be only countably many jumps in any probability distribution, it is possible to find a small ε > 0 such that a jump does not occur at p-ε. Consider a deviation strategy where a target i sets p-ε with the probability with which he used to set p, and sets p with probability zero. The net gain from such a deviation becomes
As ε converges to zero, the sum of the first four terms converges to zero but the sum of the last two terms remains positive. This leads to a contradiction because the deviation strategy leads to a lower expected loss than the assumed equilibrium strategy. □
Proof of Lemma 3
Given the assumptions limp→0c′ (p) + D < 0 and c′(pmax) = 0, the first-order condition for the minimization problem is satisfied as an equality in (0, pmax]. In other words, there exists a p ∈ (0, pmax] such that
This follows from the fact that the function c′ (⋅) + μD is continuous with limp→0c′ (p) + μD ≤ limp→0c′ (p) + D < 0 and 0 ≤ c′(pmax) + μD = μD. Since the objective function is strictly convex, such a p must be the unique solution to the minimization problem. Given that c′ (⋅) is strictly increasing, the first-order condition can be rewritten as
where c′-1(⋅) is the inverse of c′ (⋅). p(μ) must be continuously differentiable with respect to μ given that c(⋅) is twice continuously differentiable.
For a given p, it is straightforward to show that p ∈ (0, p] is also uniquely determined. The assumption D < limp→0c(p) implies
The second inequality follows from c(pmax) = 0 and 0 ≤ μ, pmax ≤ 1 while the third equality uses the fact p = argmin Lmax(p). Since c(⋅) is strictly decreasing with cp) ≤ c(p) + μpD, there must be a unique p ∈ (0, p] such that c(p) = c(p) + μpD. Given that p(μ) is continuously differentiable, so is p(μ), which is a continuously differentiable function of p. □
Proof of Proposition 1
The following claim 1 through claim 5 establish the first part of the proposition. Define M(p) ≡ c(p) + F*(p)n-1μpD. Let suppF(⋅) be the support of the distribution function F(⋅), i.e., suppF(x) ≡{x:F(x + ε)-F(x-ε) > 0 for any ε > 0}.
Claim 1 For all p′, p′′∈ suppF*(p), M(p′) = M(p′′).
Proof Suppose not. Then there exists 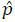 ∈ suppF*(p) such that
∈ suppF*(p) such that
Notice that the support of a distribution function is closed (see Chung, 1974). Given that suppF*(p) ⊂[0,1] is also bounded, the minimum on the right-hand side is well-defined. Let
p = {p:p = argmin M(p)}. Given that c(p) and F*(p) are both continuous, M(p) is also continuous. This means that there exists an interval (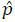 -ε,
-ε,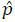 + ε) such that for all p∈(
+ ε) such that for all p∈(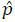 - ε,
- ε,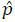 + ε), M(p) > M. Notice that
+ ε), M(p) > M. Notice that 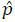 ∈ suppF*(p) implies F*(
∈ suppF*(p) implies F*(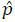 + ε)-F*(
+ ε)-F*(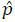 - ε) > 0. Consider a deviation strategy which assigns probability 1 to a p∈p. The net gain from such a deviation is given by
- ε) > 0. Consider a deviation strategy which assigns probability 1 to a p∈p. The net gain from such a deviation is given by
which contradicts the assumptions that F*(p) is the equilibrium strategy. □
Claim 2 F*(p) = 1 and F*(p) = 0.
Proof Define pm ≡ min p∈ suppF*(p) and pM ≡ max p∈suppF*(p). Suppose to the contrary that F*(p)<1. This implies pM > p. Given that p∈suppF*(p), the equilibrium expected loss is given by
Recall that Lmax(p) = c(p) + μpD is strictly increasing in p for p> p. If a target deviates by playing p = p with probability one, the net gain becomes
which contradicts the assumptions that F(p) is the equilibrium strategy. A similar argument establishes F*(p) = 0. Assuming F*(p) > 0 implies pm < p. Then the equilibrium expected loss must be equal to
But a target incurs at most c(p) + μpD = c(p) by playing p = p with probability one. Therefore, net gain from such a deviation becomes at least
given that c(⋅) is strictly decreasing. Again, this contradicts the assumption that F*(p) is the equilibrium strategy. □
Claim 3 F*(p-ε) < 1 for any ε > 0.
Proof Suppose not. Then it follows that pM < p. Then the equilibrium expected loss must be equal to M(pM) = c(pM) + μpMD. Consider a deviation strategy that assigns probability one to p = p. Notice that pM < p implies M(p) = c(p) + μpD. Given that Lmax(p) = c(p) + μpD is strictly decreasing in p for p < p, the net gain from such a deviation becomes
which leads to contradiction.
Given that p∈ supp F*(p), it follows that M(p)=M(p) for all p∈ suppF*(p). The equation M(p)=M(p) implicitly determines the equilibrium distribution function F*(p):
To confirm that F*(p) satisfies the requirements for a distribution function. Notice first that F*(p) = 0, F*(p) = 1. Also, for p∈(p,p)
where the inequality follows from c(p) + μpD < c(p) + μpD and c'(p) + μD < 0 for p∈(p,p). □
Claim 4 F*(p + ε) > 0 for any ε > 0.
Proof Suppose not. This implies pm > p. Then the equilibrium expected loss must be equal to M(pm) = c(pm). Given that p = pM ∈ supp F*(p), however, the equilibrium expected loss must be equal to c(p) + μpD. But this leads to a contradiction because
given that c(⋅) is strictly decreasing. □
Claim 5 F*(p′′)-F*(p′) > 0 for all p < p′ < p′′ < p.
Proof Suppose not, i.e., there exist p′, p′′∈(p,p) such that F*(p′′)-F*(p′) = 0 and p′ < p′′. Let PF ≡ {p∈(p,p): F*(p) = F*(p′) = F*(p′′)} be the preimage of F*(p′). Given that the function F*(⋅) is continuous, the set PF must be closed. Then pL ≡ min p∈PF and pH ≡ max p∈PF are well-defined. By construction, it must be that pL ≤ p′ < p′′ ≤ pH and pL, pH∈suppF*(p). Then the equlibrium expected loss is equal to
Let MF(p) ≡ c(p) + F*(p′)n-1 μpD. Given that c(p)′′ > 0, the function MF(p) is strictly convex with MF(pL) = MF(pH). This implies MF(p) < MF(pL) for all p∈(pL,pH). If a target sets any p∈(pL,pH) with probability one, however, the expected loss becomes c(p) + F*(p′)n-1 μpD = MF(p), which is smaller than the equilibrium expected loss MF(pL). This contradicts the assumption that F*(p) is the equilibrium distribution function.
For the second part of the claim, let Δ*(μ) ≡ G(θ*(μ))-μ. Then Δ*(μ*) = 0. Notice that
where the last equality follows from integrating by parts. Given that p(μ), p(μ), and (F*(p;μ))n are all continuous in μ, Δ*(μ) is also continuous. Given the continuity of Δ*(⋅), the existence of μ* is proved if one can show that Δ*(1)< 0 < limμ→0Δ*(μ). To see this, notice first that the equilibrium distribution (F*(p;μ))n becomes degenerate at p = pmax as μ→0. This implies
where the inequality follows from the assumption pmaxD> θ. Moreover, p ≤ pmax implies
therefore,
where the last inequality follows from the assumption pmaxD < θ.
To prove the uniqueness of μ*, it suffices to show that Δ*(μ) is strictly decreasing in μ. Using the envelope theorem to evaluate 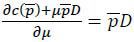 , one can show that
, one can show that
Given that 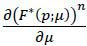 ,
, 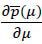 , and
, and 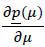 are all continuous,
are all continuous, 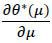 can be evaluated using Leibniz’s integral rule. This leads to
can be evaluated using Leibniz’s integral rule. This leads to
given that F*(p;μ) = 1 and F*(p;μ) = 0. Since 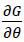 > 0, it follows that
> 0, it follows that 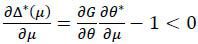 as claimed. □
as claimed. □
Proof of Lemma 4
Suppose not, i.e., there exists a set 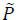 = {p:pi ≠ pj for some i, j} and Pr(p∈
= {p:pi ≠ pj for some i, j} and Pr(p∈ ) > 0. For each p =(p1,..., pn), define p′ = max{p1,..., pn}(1, . . . ,1). Consider an alternative strategy where the targets set p′ with the probability with which they used to set p. The gains from such a strategy is given by
) > 0. For each p =(p1,..., pn), define p′ = max{p1,..., pn}(1, . . . ,1). Consider an alternative strategy where the targets set p′ with the probability with which they used to set p. The gains from such a strategy is given by
since 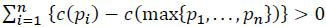 for p ∈
for p ∈ 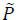 and Pr(p ∈
and Pr(p ∈ 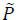 ) > 0. This implies that a strategy where Pr(p ∈
) > 0. This implies that a strategy where Pr(p ∈ 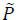 ) > 0 is never optimal, which leads to a contradiction. □
) > 0 is never optimal, which leads to a contradiction. □
Proof of Proposition 2
First, it is shown that there exists a unique μc ∈ (0,1) satisfying the beliefconsistency condition. Notice that the first-order condition
for the targets’ minimization problem holds as an equality, i.e., nc′(pc) + μD = 0 given that limp→0nc′(p) +μD < limp→0c′(p) + D < 0 and nc′(pmax) + μD ≥ 0. Since c′(⋅) is strictly increasing, this implies 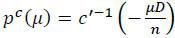 . where c′-1(⋅) is the inverse of c′(⋅) . pc(⋅) must be continuous and strictly decreasing given that c′-1(⋅) is continuous and strictly increasing. Let Δc(μ) ≡ G(θc(μ))-μ. Then the equilibrium belief μc must satisfy Δc(μc) = 0. Notice that Δc(⋅) is continuous and strictly decreasing given that θc(⋅) = pc(⋅)D is continuous and strictly decreasing while G(⋅) is continuous and strictly increasing. This implies that the solution to the equation
Δc(μ) = 0, if exists, must be unique. Given the assumption θ < pmaxD < θ, the solution does exist because Δc(0) = G(pmaxD) > 0 and Δc(1) = G(pc(1)D)-1 ≤ G(pmaxD) < 0. If μc > 0, it must be that nc′(pmax) + μcD = μcD> 0. This means pc< pmax. Also G(pminD) = G(θ) = 0 implies pmin < pc.
. where c′-1(⋅) is the inverse of c′(⋅) . pc(⋅) must be continuous and strictly decreasing given that c′-1(⋅) is continuous and strictly increasing. Let Δc(μ) ≡ G(θc(μ))-μ. Then the equilibrium belief μc must satisfy Δc(μc) = 0. Notice that Δc(⋅) is continuous and strictly decreasing given that θc(⋅) = pc(⋅)D is continuous and strictly decreasing while G(⋅) is continuous and strictly increasing. This implies that the solution to the equation
Δc(μ) = 0, if exists, must be unique. Given the assumption θ < pmaxD < θ, the solution does exist because Δc(0) = G(pmaxD) > 0 and Δc(1) = G(pc(1)D)-1 ≤ G(pmaxD) < 0. If μc > 0, it must be that nc′(pmax) + μcD = μcD> 0. This means pc< pmax. Also G(pminD) = G(θ) = 0 implies pmin < pc.
To see that μ*< μc, it is helpful to define μ* such that G(p(μ*)D) = μ*. Since p(⋅) and G(⋅) are both continuous with G(p(0)D) = G(pmaxD) > 0 and G(p(1)D)-1 ≤ G(pmaxD)-1 < 0, such a μ*∈(p, 1) is uniquely determined. Then it must be that μ* < μ*. To confirm, suppose to the contrary that μ* ≥ μ*. Given that G(∫[0,1] pDd(F*(p;μ*))n) = μ*, it follows
Since G(⋅) is strictly increasing, this implies ∫[0,1] pd(F*(p;μ*))n ≥ p(μ*). Notice that the distribution function (F*(p;μ))n has a support [p(μ), p(μ)] and p(μ) is strictly decreasing in μ. This implies ∫[0,1] pd(F*(p;μ*))n < p(μ*) ≤ p(μ*), which is a contradiction.
A similar argument can be used to establish μ* < μc. To see this, suppose to the contrary that μ* ≥ μc. Given that G(pc(μc)D) = μc, it follows
Since G(⋅) is strictly increasing, it must be that p(μ*) ≥ pc(μc). Consider p(μc) and pc(μc). From the first-order conditions,
which implies nc′(pc(μc)) = c′(p(μc)). But this leads to p(μc) < pc(μc) because c′(⋅) < 0 is strictly increasing. Given that p(⋅) is strictly decreasing and p(μ*) ≥ pc(μc), it follows that μ* < μc, which is a contradiction. □
Proof of Proposition 3
Characterizing the equilibrium boils down to showing that there exists a unique po∈[pmin, pc). Then μo∈[0, μc) follows immediately because pmin ≤ po < pc implies 0 = G(pminD) ≤ G(poD) < G(poD) = μc. To see that po is uniquely determined in [pmin, pc), notice first that it is never optimal to set po < pmin. The probability of an attack becomes zero once p reaches pmin. If the targets set p below pmin, therefore, they will increase the cost of investment without lowering the probability of an attack. Similarly, any po > pmax cannot be optimal, either. Otherwise, the targets will be able to reduce the risk of an attack without any extra costs of investment. Without loss of generality, therefore, the domain for the targets’ minimization problem can be restricted to p∈[pmin, pmax].
Given the assumption 2G′(θ) + G′′(θ)θ > 0. the targets’ objective function is strictly convex for p ≥ pmin because
This implies that the solution to the minimization problem must be unique. In contrast to the equilibrium with coordination only, however, the first-order condition may not hold as an equality. Differentiating the objective function with respect to p gives
The second derivative is shown to be positive, which means that Γ(⋅) is strictly increasing. There are two cases to consider: i) Γ(pmin) ≥ 0 and ii) Γ(pmin) < 0. If Γ(pmin) ≥ 0, the objective function is increasing for all p∈(pmin, pmax]. This implies that the minimum is attained at p = pmin. If Γ(pmin) < 0, the first-order condition holds as an equality, i.e., there exists a po∈(pmin, pc) such that Γ(po) = 0. To confirm, notice that
because nc′(pc) + G(pcD)D. Given that Γ(⋅) is continuous with Γ(pmin) < 0 and Γ(pc) >0, such a po∈(pmin, pc) must exist. □
Proof of Proposition 4
For a given contract (b, B, b′, B′) a target’s loss is given by
The difference with the basic model is that a target incurs a loss (or a gain, if the payment is negative) even when it is not the victim of an attack. The loss of a target will depend on whether it is the victim of the attack and also whether the attack was successful or not. The second term on the right-hand side then gives a target’s expected loss from an attack. The joint loss of the targets can be obtained by adding all individual losses:
Due to the budget-balancing conditions, the transfer payments cancel each other out once they are summed up across all targets. Consequently, the expression for the targets’ joint loss is exactly the same as the one in the basic model. Given that the terrorist cares only about the targets’ joint loss and not its distribution, this implies that contracting does not change the terrorist’s objective function, either.
Given a contract, the equilibrium of the game is found where the terrorist and the
targets play their optimal strategies and the targets’ belief becomes consistent with
the terrorist’s equilibrium strategy. To differentiate it with the equilibrium without
contracting, μ**, θ** and 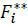 will be used to denote the equilibrium belief and the strategies.
will be used to denote the equilibrium belief and the strategies.
Lemma 5 In any equilibrium with contracting, μ** > 0.
Proof Suppose to the contrary that μ** = 0, i.e., the targets believe that an attack never occurs in equilibrium. Then it is never optimal for a target to choose a p < pmax with a positive probability. This implies
Notice that the belief consistency requires G(θ**(μ**)) = μ**. But this leads to a contradiction because
where the last inequality follows from the assumption θ < pmaxD. □
Recall that the first best may require μo = 0, i.e., there should be no attack by the terrorist. The lemma show therefore that the targets’ problem cannot be solved entirely by contracting. The question is then whether the targets may achieve the first best if it does not require a complete deterrence. A necessary condition is given by the next lemma.
Lemma 6 If 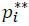 = p** for all i, then p**(D + B) + (1-p**)B′ = p**b + (1-p**)b′.
= p** for all i, then p**(D + B) + (1-p**)B′ = p**b + (1-p**)b′.
Proof Suppose not. Then there are two cases to consider: i) p**(D + B) + (1-p**)B′ > p**b + (1-p**)b′ and ii) p**(D + B) + (1-p**)B′ < p**b + (1-p**)b′. In the first case, a target may deviate by setting p′ = p**-ε for a small ε > 0. By doing so, the target becomes the strongest target with certainty. The net gain from the deviation becomes
As ε gets smaller, the first two terms approach zero but the last term remains positive. This contradicts the assumption that p** is the targets’ equilibrium strategy. A similar argument can be applied to the case p**(D + B) + (1-p**)B′ < p**b + (1-p**)b′. One may consider a deviation p′ = p**+ε. The deviant becomes the weakest target in this case. Then the net gain is given by
As ε becomes smaller, the first two terms approach zero but the last term remains positive. Again, this leads to a contradiction. □
The meaning of the condition becomes clear once a target’s objective function is examined more closely. If the targets set the same p** in equilibrium, which must be the case if the equilibrium achieves the first best, target i’s expected loss is given by
The function Es[Li(pi, 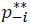 , s)] is continuous except for a potential discontinuity at pi = p**. Conditional on there being an attack, a target incurs a loss of {pi(D + B) + (1-pi)B′} if it is the victim. Otherwise, the loss becomes p**b + (1-p**)b′. Hence the condition in the lemma requires that a targets should be indifferent
between being and not being the victim of an attack. If not, a target will deviate
by slightly lowering (or raising) its p to get the better payoff. Once the condition is satisfied, the function Es[Li(pi,
, s)] is continuous except for a potential discontinuity at pi = p**. Conditional on there being an attack, a target incurs a loss of {pi(D + B) + (1-pi)B′} if it is the victim. Otherwise, the loss becomes p**b + (1-p**)b′. Hence the condition in the lemma requires that a targets should be indifferent
between being and not being the victim of an attack. If not, a target will deviate
by slightly lowering (or raising) its p to get the better payoff. Once the condition is satisfied, the function Es[Li(pi, 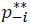 , s)] becomes continuous for all pi.
, s)] becomes continuous for all pi.
A contract induces the first-best if 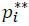 = po, i.e., each target sets po in equilibrium. Then it must be that
= po, i.e., each target sets po in equilibrium. Then it must be that
For the strategy to be optimal, any deviation must result in higher expected loss. Examining the target’s expected loss reveals that setting any p < po is never profitable. Given that all other targets set po lowering p unilaterally will only increase the cost of investment without changing the probability that an attack becomes successful.
A deviation by setting a p > po, on the other hand, may reduce a target’s expected loss. One way to prevent such a deviation is to align the optimality condition of individual targets with the one that minimizes their joint expected loss. Assuming that an attack occurs with a positive probability, i.e., μo = G(poD) > 0, the first best solution is determined by
or
On the other hand, a target’s expected loss will be minimized at po in equilibrium if it is increasing in pi for all pi > po. Differentiating the function Es[Li(pi, 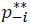 , s)] with respect to pi and evaluating it at p** = po gives c′(pi) + μo(D + B-B′). This implies that a target will never deviate from the first-best solution if
, s)] with respect to pi and evaluating it at p** = po gives c′(pi) + μo(D + B-B′). This implies that a target will never deviate from the first-best solution if
for pi > po Given the convexity of c(⋅), the left-hand side of the inequality increases with pi. Hence the condition will be satisfied for all pi > po if the inequality holds at pi = po, i.e.,
Comparing the expression with reveals that this inequality is reduced to
By construction, the first best can be supported as an equilibrium if a contract satisfies (1) and (3) along with the two budget-balancing conditions. As long as other targets are doing the same, it will be optimal for a target to set p = po. Given the targets’ strategy, the terrorist should initiate an operation only when θ ≤ θo = poD. The targets’ belief μo is then consistent with the terrorist’s strategy because μo = G(poD). Given that the condition (3) is in inequality form, however, the optimal contract is not determined uniquely. In case (3) holds as a strict inequality, each target's expected loss must be strictly increasing at p = po. This implies that the targets would reduce their expected loss further if they could collectively choose to lower their p’s. Then a strong refinement in the spirit of Aumann (1959) may eliminate such a possibility and hence resolve the indeterminacy.
Now, for the proof of proposition 4, notice first that any budget-balancing contract that implements the first best must satisfy
Solving for b, B, and B′ gives,
Then the expected loss of target i can be expressed in terms of b′ only. Given that pj = po for all j ≠ i, this gives
For pi = po to be optimal, 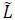 (pi;b′) must be increasing in pi at pi = po, i.e.,
(pi;b′) must be increasing in pi at pi = po, i.e.,
It is easy to confirm that the inequality holds as an equality at 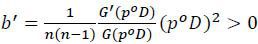 . Given that
. Given that 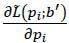 is increasing in pi, this implies that any contract with
is increasing in pi, this implies that any contract with 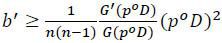 can support the first best given that b, B, and B′ are determined accordingly. □
can support the first best given that b, B, and B′ are determined accordingly. □
Proof of Corollary
For the contract to implement the first best, it must satisfy (1) which is now reduced to
Combined with the remaining budget-balancing constraint B +(n-1)b = 0, the contract can be determined completely, which is given by
Then it is straightforward to verify that the contract does not implement the first best. This is because the contract violates (3) i.e.,
Notes
One of the games considered in Bier et al. (2007) has the same structure as the second- and third stage of the game analyzed in this article. In their set-up, the terrorist's preference is assumed to be a private information, which opens up the possibility that equilibrium may exist in pure strategies. They claim indeed that equilibrium must be pure, and characterize such an equilibrium. But their proof, which resorts to the convexity of the targets’ cost function, is incomplete at best. This is because the convexity cannot rule out a mixed equilibrium with a connected support although it does rule out an equilibrium with a “gap” in the support.
More specifically, the fixed numbers of “informed” and “uninformed” consumers in Varian (1980) provide natural boundaries for the equilibrium support, which is not the case in this paper where the boundaries need to be determined endogenously from the targets' best response.
Although the symmetric equilibrium of the game is completely characterized by the proposition, technically it is not unique in the usual sense. Given that the targets’ strategy involves mixing, any distribution function that differs from F*(p;μ*) on a set of measure zero will also be an equilibrium strategy. Hence, the uniqueness in this case should be the one among these equivalent classes of functions.
References
, & (2005). Counterterrorism: A Game Theoretic Analysis. Journal of Conflict Resolution, 49, 183-200, https://doi.org/10.1177/0022002704272863.
, , & (2007). Choosing What to Protect: Strategic Defensive Allocation Against an Unknown Attacker. Journal of Public Economic Theory, 9, 563-587, https://doi.org/10.1111/j.1467-9779.2007.00320.x.
, & (2005). IDS Models of Airline Security. Journal of Conflict Resolution, 49, 201-217, https://doi.org/10.1177/0022002704272833.
, & (2003). The Ecology of Terror Defense. Journal of Risk and Uncertainty, 26, 201-229, https://doi.org/10.1023/A:1024167124083.
(2004). The Investment Problem in Terrorism. Economica, 71, 449-459, https://doi.org/10.1111/j.0013-0427.2004.00379.x.
, & (2005). Insurance, Self-protection, and the Economics of Terrorism. Journal Public Economics, 89, 1891-1905, https://doi.org/10.1016/j.jpubeco.2004.06.008.
, & (2004). Too Much of a Good Thing?: The Proactive Response Dilemma. Journal of Conflict Resolution, 48, 657-671, https://doi.org/10.1177/0022002704268278.
(2003). Collective Action and Transnational Terrorism. World Economy, 26, 779-802, https://doi.org/10.1111/1467-9701.00548.
, & (2004). An Economic Perspective on Transnational Terrorism. European Journal of Political Economy, 20, 301-316, https://doi.org/10.1016/j.ejpoleco.2003.12.007.
(2005). Political and Militant Wings within Dissident Movements and Organizations. Journal of Conflict Resolution, 49, 218-236, https://doi.org/10.1177/0022002704272865.
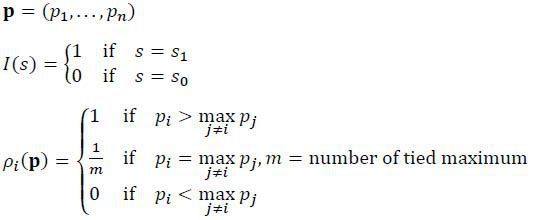
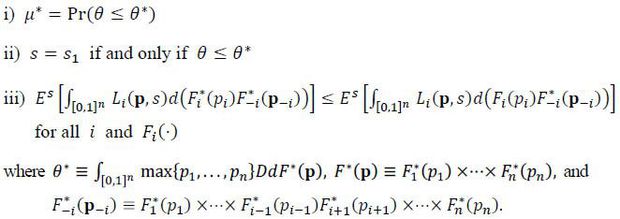
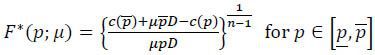
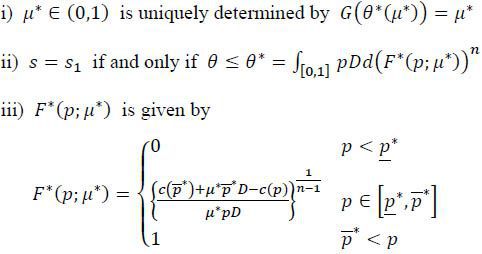


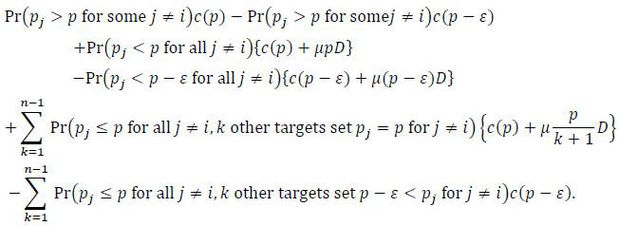
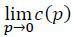 > D ≥ c(pmax) + μpmaxD ≥ c(
> D ≥ c(pmax) + μpmaxD ≥ c(
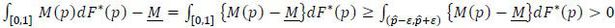
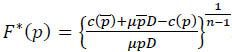
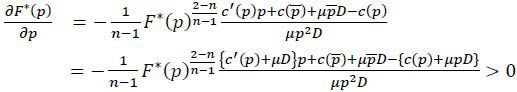
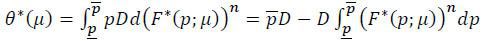
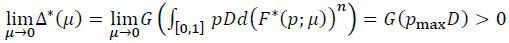
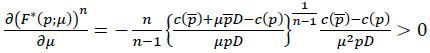
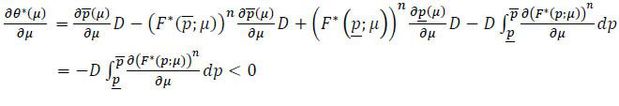
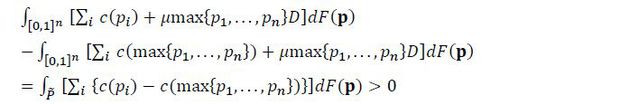
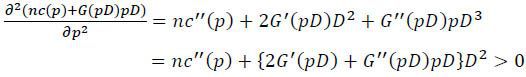
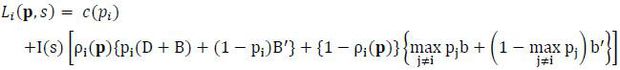
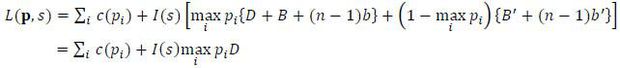
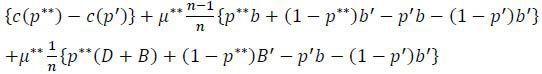
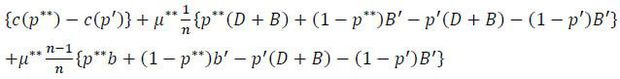
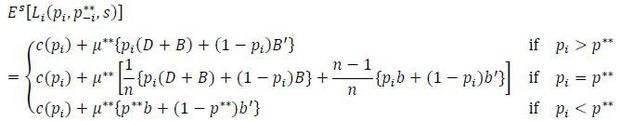
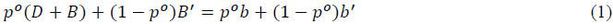
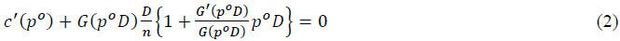

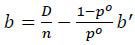
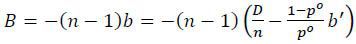
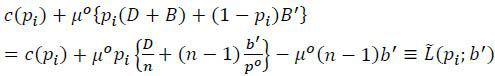
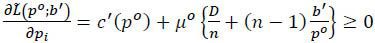
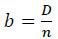
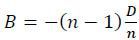 .
.
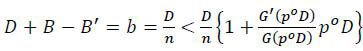 . □
. □