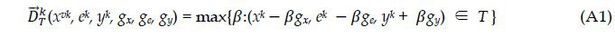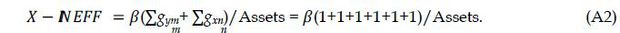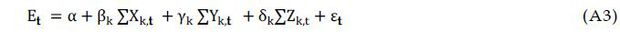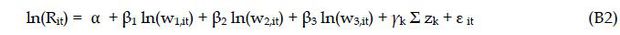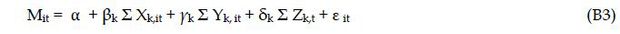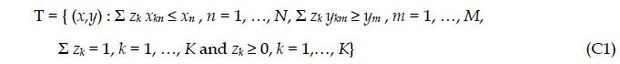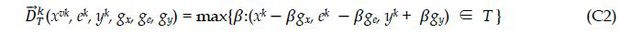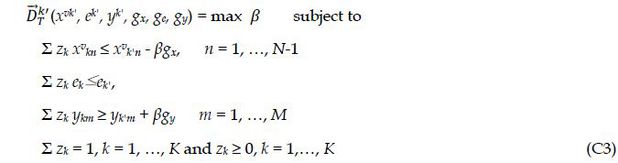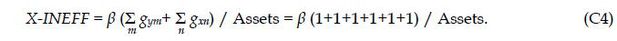What Happened to Efficiency and Competition after Bank Mergers and Consolidation in Korea?
Abstract
Market concentration in the Korean banking industry has markedly increased since the financial crisis of 1997-1998 because of M&As, P&As, and consolidation of banks. With this change, there has been a growing concern over market power in the Korean banking sector. We examine the effects of market concentration on bank efficiency and competition for the period of 1992-2006. Three different indicators of bank inefficiency are used in this study, including X-inefficiency that is derived from the directional technology distance function. The level of competition is measured by both the H-statistic of the Panzar-Rosse model and the level of the net interest margin and its standard deviation.
Empirical results indicate that market concentration has not improved bank efficiency through scale economies or scope economies. Instead, recent mergers, acquisitions and consolidation of banks resulted in an increase in inefficiency measured by the three different indicators: X-inefficiency, labor inefficiency and asset inefficiency. While an increase in market share of individual banks improved bank efficiency, an increase in the overall market concentration ratio resulted in lower efficiency. Our study also finds that the Korean banking sector has been monopolistically competitive throughout the sample period except for the crisis period according to the H-statistic. Although an increase in market concentration ratio has not changed the overall level of bank competition, it has a positive significant effect on the level of the average interest margin.
Keywords
Bank Consolidation, Market Concentration, Competition, Efficiency, Korean Banks, 은행 통합, 시장집중, 은행 경쟁도, 은행 효율성, 한국의 은행산업
JEL Code
G21, L10
Ⅰ. Introduction
During the last two decades a fundamental change in banking market structure occurred in many countries through mergers and acquisitions (M&As), purchase of assets and assumptions of liabilities (P&As) and consolidation under financial holding companies. Financial deregulation and financial globalization accompanied by advance in information technology triggered fierce competition among banks and necessitated M&As, P&As and consolidation in the world to reduce risk through business diversification and take advantage of scale economies. Korea is no exception. Over the last twenty years the Korean banking system went through many changes: financial deregulation, financial crisis, and restructuring. In this process, market concentration initially decreased as the number of banks increased due to financial deregulation prior to the Asian financial crisis of 1997-1998, but, after the crisis, the concentration ratio increased because of a decline in the number of banks due to bank closures and creation of mega banks through bank mergers, acquisitions and consolidation. The structural reform after the financial crisis introduced the financial holding company system and allowed mergers among larger banks, resulting in a few super-size banks.
Park and Weber (2006a) estimate Korean bank efficiency and productivity change for the period 1992 to 2002. These estimates are derived from the directional technology distance function. Their method controls for loan losses that are an undesirable by-product arising from the production of loans and allows the aggregation of individual bank inefficiency and productivity growth to the industry level. Their findings indicate that technical progress during the period was more than enough to offset efficiency declines so that the banking industry experienced productivity growth. Park (2009) examines market concentration and competition in the Korean commercial banking market for the period of 1992-2004. The H-statistic of the Panzar-Rosse model indicates that the Korean commercial banking market was monopolistically competitive during the pre-crisis period and the post-crisis period with temporary deviation to the level of perfect competition during the crisis period. However, the crisis period could not pass the equilibrium condition test. The author concludes that increased concentration has not lessened the overall level of competition in Korea.
This paper is built upon Park and Weber (2006a) and Park (2009), but extends further to examine the effects of M&As, P&As and consolidation and the subsequent increase in market concentration on efficiency and competition in the Korean banking sector, using 1992-2006 data. While the previous two papers focus on measurement and changes in the levels of efficiency and competition of Korean banks, this paper examines what are the main determinants of the levels of efficiency and competition and how significant the effects of market concentration are in the Korean banking industry. Furthermore, updated data are used in this study: data of four more years compared to Park and Weber (2006a) and data of two more years data compared to Park (2009). Section 2 describes the activities of M&As, P&As and consolidation occurring in the Korean banking sector and the resulting trend in market concentration during the sample period. Section 3 introduces the directional technology distance function used to estimate efficiency and analyzes the effects of market concentration on efficiency. Section 4 discusses the method used to measure the degree of competition and then estimates the effects of market concentration on competition. In the final section we offer a summary of our work and draw conclusions.
Ⅱ. M&As, P&As, Consolidation and Market Concentration
Market concentration can be measured in a number of ways. The most straightforward method is to calculate what share of the industry’s output is sold by a few dominant firms, typically measured by the sum of top k-firm market shares (CRk). Another formula now widely used is the Herfindahl-Hirschman index (HHI). HHI is measured by the sum of the squares of each firm’s market share in an industry. The top k-firm concentration ratio (CRk) was previously used by the Fair Trade Commission in Korea in determining the degree of anti-competition of a proposed merger until it adopted HHI as a new criterion a few years ago. Previously a market with CR1 greater than 50% or CR3 greater than 70% was regarded as a highly concentrated market. While the Fair Trade Commission in Korea and the Department of Justice and the Federal Trade Commission in the US use HHI in their antitrust policy currently, their classification of markets is somewhat different. Both agree on the classification of highly concentrated markets as those with HHI above 2,500. However, they differ in classifying unconcentrated markets: HHI below 1200 in Korea while HHI below 1500 in the US.
Table 1 presents the trend of market concentration in the Korean banking industry by the number of banks, HHI and CR3 of bank total assets, bank total loans and bank total deposits for the period of 1992-2006. There was a decreasing trend of market concentration in all three variables until the Asian financial crisis of 1997-1998. This trend began in 1982 as financial deregulation induced entry of new banks and caused fierce competition among the existing banks. Until the Korean government introduced a series of financial reforms in 1982, the number of national commercial banks was limited to five while ten much smaller regional banks were allowed in order to stimulate regional economic development. With financial liberalization, the number of national commercial banks increased from five to fourteen in 1992, leading to a decrease in market concentration. Just before the crisis, there was a concern of overbanking in Korea. However, closures of insolvent banks and mergers with blue-chip banks after the crisis resulted in a drastic increase in the market concentration ratio.
<Table 1>
Trend of Market Concentration in the Korean Banking Industry
Note: 1) Total assets, loans and deposits include both banking accounts and trust accounts.
2) The correlation coefficients among the three HHIs are 0.995 or higher, and the correlation coefficients among the three CR3s are 0.984 or higher.
The change in market concentration after the crisis reflects the structural reform in the banking sector carried out by the Korean government. The Korean government began a two-phase financial restructuring. In its first-phase restructuring from 1998 to 2000, three types of merger occurred. First, five insolvent banks were merged into five sound banks in the form of P&As in 1998. Dongwha Bank was acquired by Shinhan Bank, Daedong Bank by Kukmin Bank, Dongnam Bank by the Housing and Commercial Bank, Kyungki Bank by Hanmi Bank, and Chung Chong Bank by Hana Bank. Second, involuntary mergers between three groups of relatively sound banks were initiated by the Korean government. They are the merger of Commercial Bank of Korea and Hanil Bank to form Hanvit Bank, the merger of Choongbuk Bank and Kangwon Bank into Cho Heung Bank, and the merger of the Long-term Credit Bank into Kukmin Bank in 1999. Third, there was one voluntary merger of two privately-owned banks, Boram Bank merging into Hana Bank. The second and third types of mergers are in the form of M&As.
The second-phase restructuring that began in 2001 focused on restoring bank profitability. This structural reform also introduced the financial holding company system and allowed mergers among larger banks, resulting in a few super-size banks. In 2001, Woori Holding Co. consolidated the following four banks: Hanvit Bank, Kwangju Bank, Kyungnam Bank and Peace Bank. In 2002, there was a merger of Kukmin Bank and the Housing and Commercial Bank, and Shinhan Financial Holding Co. consolidated Shinhan Bank and the Bank of Cheju. In 2005, Hanmi Bank was acquired by Citi Bank and renamed as Korea Citi Bank. In the same year, the Standard and Charter Bank acquired Korea First Bank that was nationalized in 1998 and sold to the Newbridge Capital in 1999 and renamed it as SC Korea First Bank. In 2006, Cho Heung Bank was merged into Shinhan Bank.
As a result of P&As, M&As and consolidation, the number of banks was reduced and the average asset size of banks increased. While a few mega banks were established through mergers, acquisitions and creation of financial holding companies, small regional banks remained unchanged. Thus the Korean banking industry experienced polarization in bank size, leading to greater market concentration. Some observers are concerned that this policy may have a negative effect on competition and efficiency in the Korean banking industry. The post-crisis period is also characterized by increasing market share by foreign banks and increasing foreign ownership share of domestic banks.
In summary, the Korean banking sector prior to the crisis can be regarded as a non-concentrated market with HHI less than 1,000 in total assets, total loans and total deposits according to either the Korean or the US horizontal merger guidelines. After the crisis, particularly after the second-phase restructuring in 2001, the Korean commercial banking market became a moderately concentrated market with HHI ranging between 1,300 and 1,500 according to the Korean antitrust guideline. Although not reported in the table, HHI is in excess of 1800 in some specific sub-markets such as loans to households and deposits in foreign currency. HHI figures of Korea banks are higher than those of banks in other OECD countries of a similar population size. For example, HHI of Spanish banks was in the 700s and HHI of Italian banks was in the 600s according to the 2000 data of the European Central Bank. Will creation of mega banks contribute to improving efficiency and overall competitiveness of the Korean banking industry? Or will this have a negative effect on competition and efficiency. This paper discusses these issues and investigates the effects of market concentration on efficiency and competition.
Ⅲ. Effects of Market Concentration on Efficiency
There are several methods for estimating efficiency. A frontier cost or production function is typically used to estimate efficiency (or inefficiency). A stochastic frontier approach based on parametric estimation decomposes the error term into an inefficiency component and a random component. There are two stochastic approaches: distribution-free and distribution-specific. If a distribution-free approach is to be used as in Berger (1995), then the differences among banks are assumed to be stable over time. The distribution-free approach requires that banks be in existence for the entire sample period. It is difficult to apply this approach in the case of the Korean banking sector for the period of 1992-2006 because of frequent bank entry and exit during this period. If a distribution-specific approach is used as in Maudos (1998), then it is necessary to know the distribution for both components of the error term. Without prior knowledge of the distribution, arbitrary assumptions about its shape are made in most studies.
As a non-parametric approach, data envelopment analysis (DEA) is frequently used. This approach has the advantage of identifying best practices based upon observed costs rather than some hypothetical average derided from a given functional form. The DEA approach assumes that any deviation from minimum cost is due entirely to inefficiency. Using a non-parametric directional technology distance function, Park and Weber (2006a) estimated efficiency change in the Korean banking industry and Park and Weber (2006b) measured X-inefficiency of individual banks in Korea.
Following Park and Weber (2006a) and Park and Weber (2006b), we define the directional technology distance function for each bank as
where variable inputs are contracted in the direction gx, equity capital is contracted in the direction ge, and outputs are expanded in the direction of gy. A bank that produces on the frontier is efficient with 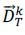 (xvk, ek, yk, gx, ge, gy) for the direction (gx, ge, gy). A value of
(xvk, ek, yk, gx, ge, gy) for the direction (gx, ge, gy). A value of 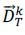 (xvk, ek, yk, gx, ge, gy) > 0 indicates inefficiency for the g-directional vector, and this value is used
in this study as X-inefficiency.
(xvk, ek, yk, gx, ge, gy) > 0 indicates inefficiency for the g-directional vector, and this value is used
in this study as X-inefficiency.
For estimation, we assume that Korean banks produce three desirable outputs using three inputs. The desirable outputs are commercial loans, consumer loans and securities. The three variable inputs are full-time labor, physical capital which equals the asset value of premises and fixed assets, and total deposits. Assuming that equity capital (e) is fixed exogenously by bank regulators and owners, we sum inefficiency over the outputs and inputs and divide by total assets.
We choose gy=(1,1,1) and gx=(1,1,1) so that the estimate of inefficiency is the simultaneous unit expansion in the three outputs and unit contraction in the three inputs that is feasible, given the best-practice. See Appendix 1 for more detailed discussions.
Alternatively, a simple, though rudimentary, approach is to approximate operating efficiency directly from the financial statements of each bank. We use a proxy for labor inefficiency or operating inefficiency: the operating expenses per employee. Similarly, we use a proxy for asset inefficiency: the operating expenses divided by total assets. The ratio of total loans to employees is suggested as a measure of operating inefficiency by Koch and MacDonald (2003). However, with deregulation and universal banking practice, the financial intermediation function of banks through loans has weakened. Therefore, it would be desirable to use total assets that include securities, foreign exchanges and other investments in addition to loans.
To examine the effects of market concentration on efficiency (or inefficiency) we estimate the following regression equation.
where Et = different efficiency (or inefficiency) indicators of bank i at time t, Xk,it=bank specific variables of bank i at time t, such as BIS equity ratio, NPL(non performing loans) SHARE, BRANCH and a dummy variable for regional banks, Yk,t = market power variables of bank i at time t, such as the market share and HHI. Zk,t = macroeconomic variables such as economic growth rate, inflation rate and a dummy variable for the crisis period. We use three different indicators of efficiency (or inefficiency) indicators: X-inefficiency obtained from estimation of equation (A2), labor inefficiency measured by the operating expenses per employee, and asset inefficiency measured by the operating expenses divided by total assets. We use panel data including all Korean national and regional banks in operation in any year during the period of 1992-2006. Data used in this study are from the Bank Management Statistics by the Bank of Korea and from the financial statements of individual banks.
Table 2 shows summary descriptive statistics for the major variables used in this study. The BIS risk-adjusted ratio of equity capital to total assets (BIS) is used as a control variable for management risk or for the impact of leverage on efficiency. The BIS risk-adjusted capital ratio is calculated according to the Bank of International Settlements guidelines, which assign varying risk weights to different types of assets. The ratio of non-performing loans to total loans (NPL SHARE) is included to control for the risk effect. The number of branches (BRANCH) is included to account for the effect of bank networks. A dummy indicator variable is defined as 1 for regional banks and 0 for national banks to see the effect of being a regional bank. Market share is measured for three different types of assets or liabilities; assets share, loans share and deposits share are the bank’s share of total industry assets, loans and deposits respectively. HHI that measures the degree of market concentration equals the sum of the squares of each bank’s market share of total industry assets, loans or deposits. INTREST MARGIN, the net interest margin, is the difference between the interest rates on loans and securities and the interest rates on deposits and borrowings. This variable is estimated by the average earnings on assets minus the average interest expenses on assets. Two macroeconomic variables, economic growth rate and inflation rate, and one macroeconomic dummy variable indicating the financial crisis period are used to see macroeconomic effects. The period of 1997-1999 is regarded in this study as the crisis period. Even though the currency crisis was over in 1998, the bank crisis continued through 1999.
Table 3A and Table 3B present the estimated results of equation (A3). In the estimation of panel data, application of ordinary multiple regression techniques may result in omitted variable bias. Hsiao (1986) demonstrated that pooled OLS results in biased and inconsistent coefficient estimates because omitted cross-section-specific variables may be correlated with the explanatory variables. Use of either a fixed-effects model or a random-effects model can solve this problem. A fixed effects model is commonly used to control for omitted variables that differ between banks but are constant over time while a random effects model is used to control for some bank-variant omitted variables and other time-variant omitted variables. In the absence of prior knowledge about omitted variables, we estimate both models and run the Hausman test comparing fixed effects vs. random effects. Based on the Hausman test, we report the fixed effects model only in the following table. The fixed effects model is usually regarded as more appropriate than random effects model when population data instead of sample data are used as in our study.
<Table 3A>
Panel Regression Results of Equation (A3) Dependent Variables: Labor Inefficiency and Asset Inefficiency, n=285
Note: 1) Estimation results of fixed effects model. The coefficients of the constant under the fixed effects model are not reported here
2) t values are shown in parentheses. * and ** indicate significance at the 5% and 1% levels respectively.
<Table 3B>
Panel Regression Results of Equation (A3) Dependent Variables: X-Inefficiency, n = 285
Note: 1) Estimation results of fixed effects model. The coefficients of the constant under the fixed effects model are not reported here
2) t values are shown in parentheses. * and ** indicate significance at the 5% and 1% levels respectively.
Market power variables show interesting results. An increase in market share by individual banks contributes to a decrease in X-inefficiency, labor inefficiency and asset inefficiency while an increase in market concentration causes greater inefficiency. The opposite signs of SHARE (individual bank’s market share) and HHI (overall market concentration level) seems to be contradictory, but can be explained. Under the efficient structure hypothesis, efficient banks have higher profits and larger market shares, thus negative correlation between market share and inefficiency. On the other hand, as overall market concentration level increases, the degree of competition among banks as well as their efforts to be efficient are lessened.
When we add the square term of HHI in the regression equation, significant negative coefficients are obtained for all the models. Therefore, their relationship is not completely linear, but of an inverse U-shaped curve, indicating that economies of scale leading to operating efficiency kick off at a certain level of market concentration. Appendix 2 shows the estimated results of model A3 with addition of HHI2 (assets).
Among the bank specific variables, BIS turns out to be insignificant in influencing operating efficiency, asset efficiency or X-efficiency. NPL SHARE has definitely a positive effect on operating costs and thus inefficiency as expected. The more branches, the higher operating cost per worker or asset. Being a regional bank does not affect X-inefficiency or asset inefficiency, but it has a significant negative effect on labor inefficiency. Regional banks are less prestigious and less competitive compared to national banks, and they tend to spend less on employee compensations and other overhead costs. However, lower labor cost does not necessarily imply higher labor productivity or higher profitability. Park and Weber (2006b) show that a dummy variable representing national banks has a positive and significant coefficient in explaining Koran bank profitability.
Among the macroeconomic variables, a dummy variable representing the crisis period stands out. In all nine different models, CRISIS has a positive significant effect on bank inefficiency. Both the GDP growth rate and the inflation rate show expected coefficient signs, a negative effect of the GDP growth rate on inefficiency and a positive effect of the inflation on inefficiency. However, significance of the coefficients varies among different model specifications. The explanatory power (Adjusted R2) of Models 1-6 is very high and that of Models 7-9 is acceptable. In summary, empirical results indicate that market concentration has not improved bank efficiency through taking advantage of scale economies or scope economies. Instead, recent mergers, acquisitions and consolidation of banks led to greater inefficiency in terms of X-inefficiency, labor inefficiency and asset inefficiency.
Ⅳ. Effects of Market Concentration on Competition
In this section we examine the effects of market concentration on the level of competition among banks. Following Panzar and Rosse (1987), the degree of competition can be measured as the H-statistic which is the sum of the elasticities of the revenue with respect to input prices.
where wi is ith input price. Panzar and Rosse (1987) show from the profit maximization condition that the H-statistic is equal to unity (H = 1) in a perfectly competitive market, and less than or equal to zero (H ≤ 0) under monopoly. Although the Panzar-Rosse article also shows that 0<H<1 could be consistent with oligopolistic behavior, it is common to regard 0<H<1 as the condition of Chamberlinian monopolistic competition. The H-statistic can be derived from the following reduced-form revenue equation.
where Rit is bank i’s revenue at time t, w1 is the input price of labor, w2 is the input price of capital, w3 is the input price of funds, and zk is a vector of control variables affecting the bank’s revenue function.
The H-statistic is the sum of β1, β2 and β3. w1,it (The unit labor cost) is measured by the ratio of personnel expenses to the number of employees, w2,it (the unit capital cost) is measured by the ratio of depreciation allowance and other maintenance costs to total fixed assets, and w3,it (the unit funding cost) is measured by the ratio of interest expenses to the sum of total deposits and borrowings. Several control variables are included in the model. Total assets (ASSET) are included to see the size effect. BRANCH, even though it may show the effect of bank networks, is not included in the model because of its high correlation with ASSET. The ratio of non-performing loans to total loans (NPL SHARE) is included to control for the risk effect. The BIS risk-adjusted capital ratio (BIS) is alternatively used as a control variable for credit market and operational risk. There has been weakening of the financial intermediation function of banks in Korea over time. The ratio of non-interest revenue to total revenue (NINT) is included to reflect the effect of changing financial intermediation or diversification. Traditionally Rit (revenue) is typically measured by interest revenue or its ratio to total assets, presuming that the main function of banks is financial intermediation. However, with weakening of financial intermediation in recent years and diversification of bank assets, total revenue or its ratio to total assets is used in some studies. In this study we use both interest revenue (IR) in log and total revenue (TR) in log as the dependent variable.
In regard to the relationship between concentration and competition in the Korean banking sector, Kim (2003) measures competition using the Bresnahan-Lau method of Bresnahan (1989) and Lau (1982) based on aggregate monthly data from 1996 to 2002 and finds that the pricing behavior of Korean banks during this period is consistent with perfect competition and that they behave more competitively even after the increase in concentration ratio. On the other hand, applying the Panzar-Rosse method, Lee and Lee (2005) find that the Korean banking market shows monopolistically competitive behavior for both the period of 1992-1997 and the period of 1998-2002 while market competition weakened significantly over the latter period. Park (2009) estimated the H-statistic with the data from Korean banks for the period of 1992-2004 and found that the Korean banking industry exhibits monopolistically competitive behavior except for the Asian financial crisis period. This study extends Park (2009) further by adding data of two more years when bigger mergers occurred. In addition, we not only estimate the degree of competition, but also examine what are the major determinants of the degree of competition. Even though the fixed effects model is usually regarded as more appropriate than random effects model when population data instead of sample data are used as in our study, we use both fixed and random effects models for comparison purpose.
The estimation results of the tests of competitive condition (the H-statistic) are given in Table 4. The Wald test rejects the hypothesis of monopolistic market structure (H=0) at the 1% level. It also rejects the hypothesis of perfectly competitive market structure (H=1) at the 1% level. Bikker et al. (2006, 2009) reported that overestimation of H-statistic is possible in the Panzar-Rosse model when the regression includes a scale variable such as the asset size. However, in this study, the H values, with exclusion of ASSET from the model, show similar test results with no indication that inclusion of a scale explanatory variable causes overestimation of the level of competition (See Appendix 3). w1,it and w3,it are positive and statistically significant, indicating that an increase in unit costs of labor or funds leads to higher revenue. w2,it is not statistically significant. When the scale variable, ASSET, is excluded, the unit capital cost exerts significant positive effect on revenue. All control variables have expected signs.
<Table 4>
Estimation Results of Equation (B2) Dependent variables: lnIR and lnTR, n=285
Note: 1) The coefficients of the constant under the fixed effects model are not reported here.
2) t values are shown in parentheses. *, ** and *** indicate significance at the 10%, 5% and 1% levels respectively.
To see how the H values changed over time, the H-statistics are estimated for moving three-year time periods, that is, 1992-1994, 1993-1995, 1994-1996 and so on. The estimation results of the H values that are reported in Table 5 along with HHI indicate that market concentration did not affect the competition level in the Korean banking industry. The correlation coefficient between HHI and the H statistic for lnIR is −0.002 while correlation coefficient between HHI and the H statistic for lnTR is −0.196, which indicates no or very low correlation between market concentration and competition.
<Table 5>
Market Concentration and Competition Level of Korean Banks
Note: 1) H-statistic is estimated from fixed effects models.
2) The correlation coefficient between HHI and the H statistic for lnIR is −0.002 while correlation coefficient between HHI and the H statistic for lnTR is −0.196.
For only the two periods, 1996-1998 and1997-1999, the hypothesis of perfectly competitive market structure (H=1) cannot be rejected at the 1% level. It can be inferred from the empirical results that the Korean commercial banking market was monopolistically competitive during the pre-crisis period and the post-crisis period, while its level of competition increased to the level of perfect competition during the crisis period, which might be due to breakdown of old connections among banks, making collusion more difficult. However, these two periods could not pass the equilibrium condition test.
As an alternative way of examining the degree of competition, we now turn to the interest margin. The average interest margin tends to increase when the market power in the banking industry increases. With polarization of bank size, the standard deviation of the net interest margin may also increase, resulting in higher margins for dominant banks and lower margins for less dominant banks. The data show that the average net interest margin for all banks declined during the crisis period, particularly in 1998, but returned to the pre-crisis level of about 2% in 2003 and then a little higher since then as shown in Figure 1. The standard deviation declined mildly over the period even though there were jittery fluctuations during the crisis period (from 0.766 in 1992 to 0.496 in 2006). A similar trend in both variables is found for both regional and national banks. However, a steady increase in both the interest margin and its standard deviation in the last two years may suggest that the effect of increased market power through M&As and consolidation on the interest spread might have begun to be realized as some have expressed their concerns over increased market power.
To further examine the effect of increased market concentration on the average net interest margin, we estimate the following regression equation.
where Mit = the average net interest margin of bank i at time t, Xk,it = bank specific variables of bank i at time t, such as BIS equity ratio, NPL(non performing loans) SHARE, BRANCH, and a dummy variable for regional banks, Yk, it = market power variables of bank i at time t, such as the market share and HHI. Zk,t = macroeconomic variables such as economic growth rate, inflation rate and a dummy variable for the crisis period.
Table 6 shows the estimation results of equation (B3). As explained earlier, we report the fixed effects model only because the fixed effects model is usually regarded as more appropriate than random effects model when population data instead of sample data are used as in our study. Market share or market concentration is measured for three different types of assets or liabilities: total assets, total loans, and total deposits. Their estimation results are presented in Models 1-3. Two market power variables are used: market share of each bank and HHI indicating the overall degree of market concentration. The market share, whether it is measured in total assets, total loans or total deposits, has a positive and significant effect, and so does HHI.
<Table 6>
Panel Regression Results of Equation (B3) Dependent Variable: Interest Margin, n = 285
Note: 1) Estimation results of fixed effects model. The coefficients of the constant under the fixed effects model are not reported here
2) t values are shown in parentheses. * and ** indicate significance at the 5% and 1% levels respectively.
All bank specific variables have significant effects on the average interest margin in all three models. BIS has a significant positive effect and is consistent with the signaling theory, which suggests that a higher equity ratio increases confidence among bank customers, leading to higher interest spread. NPL SHARE has a significant negative effect as expected. Loans are the major income-earning asset of banks and higher percentage of non-performing loans negatively affect the interest spread. BRANCH shows a positive and significant influence on interest spread through bank network effect.
A dummy variable differentiating regional banks (Regional banks =1) from national banks is positive and significant. The average interest margin for regional banks is usually higher than that for national banks because interest rates for SMEs typically serviced by regional banks include larger costs and risk premiums than interest rates for corporate loans typically serviced by national banks. This is evident in Figure 1. On the other hand, all macroeconomic variables have no significant effects on the average interest margin. CRISIS that has a significant effect on bank inefficiency is not significant in explaining the interest spread. The explanatory power of Models 1-3 (Adjusted R2) is very high. It can be inferred from the empirical results that the bank mergers that have taken place so far have increased market concentration and that the increase in individual bank’s market share and overall increase in market concentration is positively correlated with increased average interest margin.
Ⅴ. Conclusions
While market concentration in the Korean banking industry decreased during the pre-crisis period due to financial deregulation, it has markedly increased since the crisis of 1997-1998 because of M&As, P&As of banks and consolidation of banks under financial holding company system. With this change, there has been a growing concern over market power in the Korean banking industry. In this study we examined the effects of the increase in market concentration on bank efficiency and competition.
The collusion theory suggests that mergers and consolidation might be initiated by banks in order to extract consumer surplus, and the result would be higher prices to consumers and socially inefficient allocation of resources. Empirical results indicate that market concentration has not improved bank efficiency through scale economies or scope economies. Instead, recent mergers and consolidation of banks resulted in an increase in inefficiency regardless of different indicators of inefficiency used: X-inefficiency, labor inefficiency or asset inefficiency. While an increase in market share of individual banks improved bank efficiency, the overall market concentration ratio measured by HHI resulted in lower efficiency. These findings come with comforting news that the relationship between market concentration and inefficiency is not completely linear, but of an inverse U-shaped curve.
The bank mergers and consolidation that have taken place so far have not realized scale economies by rationalizing their operations or scope economies by rationalizing their business activities. Market concentration has not contributed to efficiency through these scale and scope effects. Instead it has resulted in rent extraction by oligopolistic banks. Our study also finds that the Korean banking industry has been monopolistically competitive except for the crisis period. Although an increase in market concentration has not changed the overall level of competition measured by the H-statistic, market concentration has raised the average interest margin. Therefore, a growing concern over market power in the Korean banking industry is worth to note.
The findings in this study are tenuous, given the following constraints. First, the Korean banking industry experienced a sudden change from a non-concentrated market to a moderately concentrated market in a very short time period and it is still in a transitory period. Second, most mergers and consolidation, especially the big ones, occurred towards the end of the sample period, and we may need data of a few more additional years to analyze the full effects of these mergers and consolidation on efficiency and competition.
Appendices
Appendix 1: Directional Technology Distance Function
To measure inefficiency we use the directional technology distance function proposed by Fare and Grosskopf (2004) which is based on Chambers, Chung, and Färe (1996), a generalization of the Luenberger (1992) benefit function. We assume that there are k = 1, …, K banks which employ xk vector of inputs to produce yk vector of outputs. The technology for each bank is written as {Tk = { (xk, yk) : inputs can produce outputs }. The piecewise linear DEA technology is written as:
The intensity variables, zk, k = 1, …, K, serve to form linear combinations of all observed banks’ inputs and outputs. The N+M inequality constraints restrict the technology in that for a particular bank no more output can be produced using no less input than a linear combination of all observed inputs and outputs. Requiring the intensity variables to sum to one allows variable returns to scale. We assume that the first N-1 inputs such as labor, capital, and deposits are variable inputs (xv) and can be used in greater or lesser amounts at the bank manager’s discretion, but that the Nth input, equity capital (e), is fixed exogenously by bank regulators and owners. Therefore, we partition bank k’s input vector as xk = (xvk ; ek).
Define the directional technology distance function for each bank as
where variable inputs are contracted in the direction gx, equity capital is contracted in the direction ge, and outputs are expanded in the direction of gy . For (xk, ek, yk) ∈ T. a value of 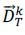 (xvk, ek, yk, gx, ge, gy)=0 indicates that the bank operates on the frontier of T and is efficient for the
direction (gx, ge, gy). A value of
(xvk, ek, yk, gx, ge, gy)=0 indicates that the bank operates on the frontier of T and is efficient for the
direction (gx, ge, gy). A value of 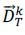 (xvk, ek, yk, gx, ge, gy) > 0 indicates inefficiency. We assume that equity capital (e) is fixed exogenously by bank regulators and owners, and therefore we choose ge = 0 so that equity capital is not scaled upon. For the DEA technology, the directional
technology distance function for bank k' is estimated as
(xvk, ek, yk, gx, ge, gy) > 0 indicates inefficiency. We assume that equity capital (e) is fixed exogenously by bank regulators and owners, and therefore we choose ge = 0 so that equity capital is not scaled upon. For the DEA technology, the directional
technology distance function for bank k' is estimated as
Figure A shows how the production technology and inefficiency are estimated from the observed input and output with an example of four banks: A, B, C, and D. The piecewise linear technology, T, is bounded by the lines HB, BD, DA, and the horizontal extension from A. Given a direction vector (gx, ge, gy) where ge. is assumed to be zero, the directional distance function is defined as (C2) and estimated via (C3). This function expands output in the direction gy, contracts inputs in direction gx, and is a measure of technical inefficiency (X-inefficiency). Banks A, B, and D produce on the frontier of T are technically efficient. Bank C operates inside the frontier and is technically inefficient.
In this study, we measure X-inefficiency by the directional distance between F and C in Figure A. For estimation, we use three inputs, which are labor, capital, and deposits, and three outputs, which are commercial loans, consumer loans, and securities. We choose gy = (1,1,1) and gx = (1,1,1) so that the estimate of inefficiency from equation (C3) is the simultaneous unit expansion in the three outputs and unit contraction in the three inputs that is feasible, given the best-practice combinations of outputs and inputs of the banks in our sample. An inefficient bank earns less revenue and incurs higher costs than it would if it operated on the frontier. We sum inefficiency over the outputs and inputs and divide by total assets.
Appendix 2. Panel Regression Results of Equation (A3) with inclusion of HHI2 as an Additional Independent Variable, n=285
References
(1995). The Profit-structure Relationship in Banking−Tests of Market-power and Efficient-structure Hypotheses. Journal of Money, Credit and Banking, 27(2), 404-431, https://doi.org/10.2307/2077876.
, , & (1996). Benefit and Distance Functions. Journal of Economic Theory, 70, 407-419, https://doi.org/10.1006/jeth.1996.0096.
(1982). On Identifying the Degree of Competitiveness from Industry Price and Output Data. Economics Letters, 10, 93-99, https://doi.org/10.1016/0165-1765(82)90122-7.
(1992). Benefit Functions and Duality. Journal of Mathematical Economics, 21, 461-481, https://doi.org/10.1016/0304-4068(92)90035-6.
(1998). Market Structure and Performance in Spanish Banking Using a Direct Measure of Efficiency. Applied Financial Economics, 8, 191-200, https://doi.org/10.1080/096031098333177.
, & (1987). Testing for ‘Monopoly’ Equilibrium. Journal of Industrial Economics, 35, 443-456, https://doi.org/10.2307/2098582.
(2009). Has Bank Consolidation in Korea Lessened Competition? Quarterly Review of Economics and Finance, 49, 651-667, https://doi.org/10.1016/j.qref.2008.02.003.
, & (2006a). A Note on Efficiency and Productivity Growth in the Korean Banking Industry, 1992-2002. Journal of Banking and Finance, 30, 2371-2386, https://doi.org/10.1016/j.jbankfin.2005.09.013.
, & (2006b). Profitability of Korean Banks: Test of Market Structure Versus Efficient Structure. Journal of Economics and Business, 58, 222-239, https://doi.org/10.1016/j.jeconbus.2005.09.003.